Nou în 
Model de logit multinomial panou-date
Modelul multinomial logit (MNL) este o metodă populară pentru modelarea rezultatelor categorice care nu au o ordonare naturală – rezultate precum ocupația, partidul politic sau alegerea restaurantului.
În datele longitudinale / de panou, observăm o succesiune de rezultate în timp. Spuneți că observăm în fiecare săptămână opțiunile de restaurant făcute de persoane. Crezi că alegerile de restaurant sunt independente de la săptămână la săptămână? Probabil ca nu. Cineva căruia îi place mâncarea italiană este probabil să aleagă un restaurant italian de mai multe ori. Aceste alegeri sunt determinate de preferințele și caracteristicile personale subiacente, dintre care unele nu sunt respectate.
Noua comandă xtmlogit a Stata se potrivește cu modelele MNL cu efecte aleatorii și cu efecte fixe condiționate pentru rezultate categorice observate în timp.
Pentru a se potrivi unui model logit multinomial cu efecte aleatorii, putem tasta
. xtset subject . xtmlogit restaurant age
și se estimează coeficienții logit multinomiali standard care țin cont de caracteristicile specifice subiectului invariante în timp, incluzând efecte aleatorii specifice fiecărui nivel de rezultat.
Cu comanda de mai sus, se presupune că efectele aleatorii sunt distribuite în mod normal și independente între nivelurile de rezultate (alegeri de restaurant), dar sunt acceptate mai multe structuri de varianță-covarianță, inclusiv o covarianță complet nerestricționată:
. xtmlogit restaurant age, covariance(unstructured)
Dacă bănuiți că efectele specifice subiectului ar putea fi corelate cu vârsta, puteți utiliza un estimator condiționat de efecte fixe pentru a explica acest lucru:
. xtmlogit restaurant age, fe
Repere
Modelarea panoului de date a rezultatelor categorice neordonate
Estimator de efecte aleatorii
- Alegerea structurii de covarianță pentru efectele aleatorii
- Independent
- Identitate
- Partajat
- Schimbabil
- Nestructurat
Estimator de efecte fixe condiționate (FE)
- Subseturile de permutare diminuează blestemul dimensionalității
Estimarea bayesiană
Erori standard robuste, cluster-robuste și bootstrap
Suport pentru date complexe ale sondajului
Să vedem cum funcționează
Dorim să aflăm dacă indivizii sunt mai susceptibili de a ieși din forța de muncă dacă au în gospodărie copii sub vârsta de cinci ani. Vom folosi un set de date (fictiv) al bărbaților și femeilor care au fost întrebați despre statutul lor de angajare la fiecare doi ani.
. use https://www.stata-press.com/data/r17/estatus (Fictitious employment status data)
Iată un extras al setului de date, care arată istoricul ocupării forței de muncă pentru trei persoane:
. list id year estatus hhchild age in 22/41, sepby(id) noobs
| id year estatus hhchild age | ||
| 5 2002 Employed Yes 38 | ||
| 5 2004 Employed No 40 | ||
| 5 2006 Employed No 42 | ||
| 5 2008 Employed No 44 | ||
| 5 2010 Out of labor force No 46 | ||
| 5 2012 Out of labor force No 48 | ||
| 5 2014 Unemployed No 50 | ||
| 6 2002 Unemployed Yes 31 | ||
| 6 2004 Employed Yes 33 | ||
| 6 2006 Out of labor force Yes 35 | ||
| 6 2008 Unemployed Yes 37 | ||
| 6 2010 Out of labor force Yes 39 | ||
| 6 2012 Unemployed No 41 | ||
| 7 2002 Out of labor force Yes 33 | ||
| 7 2004 Employed Yes 35 | ||
| 7 2006 Employed Yes 37 | ||
| 7 2008 Out of labor force Yes 39 | ||
| 7 2010 Employed No 41 | ||
| 7 2012 Employed No 43 | ||
| 7 2014 Employed No 45 | ||
Rezultatul interesului este statutul de ocupare (estatus), care are trei niveluri: Employed, Unemployed (dar care caută un loc de muncă) și Out of labor force (care nu caută un loc de muncă). Predictorul nostru de interes, hhchild, indică dacă au copii sub vârsta de cinci ani în gospodăria lor la momentul interviului.
Înainte de a ne potrivi modelului nostru, trebuie să specificăm variabila de identificare a panoului, id, utilizând xtset.
. xtset id Panel variable: id (unbalanced)
Acum putem folosi xtmlogit pentru a modela probabilitatea fiecărui tip de angajare de către hhchild, controlând în același timp efectele vârstei, venitul anual al gospodăriei (hhincome) și dacă o altă persoană semnificativă locuia și în gospodărie (hhsigno). Vom începe cu un model de efecte aleatorii (implicit) și vom folosi opțiunea rrr pentru a obține coeficienți exponențiați care pot fi interpretați ca raporturi de risc relativ.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, rrr
Fitting comparison model ...
Refining starting values:
Grid node 0: log likelihood = -4504.5591
Grid node 1: log likelihood = -4538.6352
Fitting full model:
Iteration 0: log likelihood = -4504.5591
Iteration 1: log likelihood = -4495.871
Iteration 2: log likelihood = -4490.5098
Iteration 3: log likelihood = -4490.4197
Iteration 4: log likelihood = -4490.4196
Random-effects multinomial logistic regression Number of obs = 4,761
Group variable: id Number of groups = 800
Random effects u_i ~ Gaussian Obs per group:
min = 5
avg = 6.0
max = 7
Integration method: mvaghermite Integration pts. = 7
Wald chi2(8) = 199.25
Log likelihood = -4490.4196 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.579937 .1513905 4.77 0.000 1.309414 1.906349 | |||||
| age | .9947946 .0065832 -0.79 0.430 .981975 1.007781 | |||||
| hhincome | .9954927 .0018251 -2.46 0.014 .9919221 .9990762 | |||||
| hhsigno | ||||||
| Yes | 1.642859 .1550291 5.26 0.000 1.365452 1.976625 | |||||
| _cons | .4949307 .1392991 -2.50 0.012 .2850836 .859244 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | .9607243 .1148148 -0.34 0.737 .7601038 1.214296 | |||||
| age | 1.004257 .008211 0.52 0.603 .9882918 1.02048 | |||||
| hhincome | .9696874 .0025722 -11.60 0.000 .964659 .9747421 | |||||
| hhsigno | ||||||
| Yes | 1.099323 .1310654 0.79 0.427 .8702452 1.388701 | |||||
| _cons | .8078165 .280628 -0.61 0.539 .4088963 1.595924 | |||||
| Employed | (base outcome) | |||||
| var(u1) | .8573133 .1083915 .6691459 1.098394 | |||||
| var(u2) | .7378532 .1388652 .5102376 1.067008 | |||||
Primele două secțiuni din rezultat arată estimările raportului de risc relativ ale predictorilor noștri în raport cu categoria de bază Employed. Ultima secțiune prezintă variațiile estimate ale efectelor aleatorii. În mod implicit, efectele aleatorii sunt necorelate, dar structura lor de covarianță poate fi modificată folosind opțiunea covariance(). De exemplu, corelațiile dintre efectele aleatorii pot fi estimate folosind covariance(unstructured) sau fiecare categorie poate împărtăși un efect aleatoriu comun folosind covariance(shared).
Ajustându-se în funcție de vârstă, venitul gospodăriei și având o altă persoană semnificativă acasă, riscul relativ de a ieși din forța de muncă pentru persoanele care au cel puțin un copil cu vârsta sub 5 ani în gospodărie față de faptul că nu au copii sub 5 ani în gospodărie este De 1,6 ori mai mare decât riscul relativ de angajare (IC 95% [1,3, 1,9]). Pentru a înțelege aceste efecte în termeni de probabilități, putem folosi comanda margins.
. margins hhchild Predictive margins Number of obs = 4,761 Model VCE: OIM 1._predict: Pr(estatus==Out_of_labor_force), predict(pr outcome(1)) 2._predict: Pr(estatus==Unemployed), predict(pr outcome(2)) 3._predict: Pr(estatus==Employed), predict(pr outcome(3))
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#hhchild | ||||||
| 1#No | .3025675 .0131546 23.00 0.000 .276785 .32835 | |||||
| 1#Yes | .3912476 .0120405 32.49 0.000 .3676486 .4148466 | |||||
| 2#No | .1628713 .0101131 16.11 0.000 .1430501 .1826925 | |||||
| 2#Yes | .1398537 .0079462 17.60 0.000 .1242794 .1554279 | |||||
| 3#No | .5345612 .0136994 39.02 0.000 .5077108 .5614116 | |||||
| 3#Yes | .4688987 .0116594 40.22 0.000 .4460468 .4917507 | |||||
Pentru o persoană fără copii, probabilitatea așteptată de a ieși din forța de muncă (1 # No) este 0,30, probabilitatea așteptată de a fi șomer (2 # No) este 0,16, iar probabilitatea așteptată de a fi angajată este 0,53 (3 #No). De asemenea, constatăm că persoanele cu copii în gospodărie își cresc probabilitatea de a ieși din forța de muncă cu 9 puncte procentuale. Am putut vedea cum aceste probabilități se modifică în funcție de venitul gospodăriei utilizând o comandă de marjă suplimentară și să vizualizăm rezultatele folosind marginsplot.
. quietly margins hhchild, at(hhincome=(20(20)100))
. marginsplot, by(_predict, label("Out of labor force" "Unemployed" "Employed"))
byopts(rows(1) title("Marginal probabilities of employment status"))
legend(order(4 "Child under 5 at home" 3 "No child under 5 at home"))
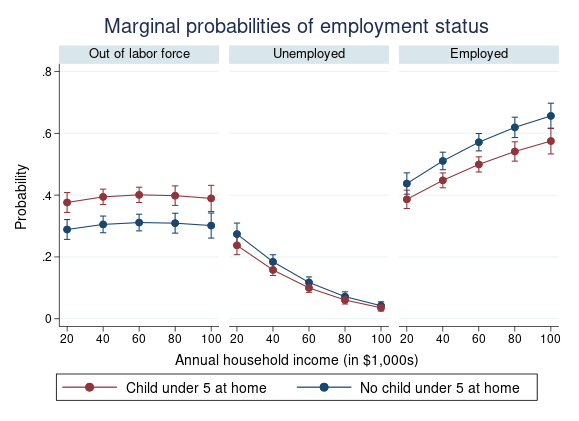
To get separate graphs for each outcome, we used the by(_predict) option in marginsplot. The rest of the options add titles and labels.
Comparing the lines within each employment category, we see that having a child at home does not have much impact on the probability of being unemployed but does influence the decision to work or to be out of the labor force.
In the model we just fit, we used random effects to account for unobserved characteristics of the individuals in our dataset. Random-effects models require that the random effects be uncorrelated with the predictors, and the random-effects MNL model is no exception. A widely used alternative is the fixed-effects estimator. To fit our model with conditional fixed effects, we simply add the fe option.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, fe rrr
note: 80 groups (451 obs) omitted because of no variation in the outcome variable over time.
Computing initial values ...
Setting up 26,168 permutations:
....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%
Fitting full model:
Iteration 0: log likelihood = -2154.4175
Iteration 1: log likelihood = -2154.2058
Iteration 2: log likelihood = -2154.2057
Fixed-effects multinomial logistic regression Number of obs = 4,310
Group variable: id Number of groups = 720
Obs per group:
min = 5
avg = 6.0
max = 7
LR chi2(8) = 67.42
Log likelihood = -2154.2057 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.784236 .2237128 4.62 0.000 1.395488 2.28128 | |||||
| age | .9977834 .0146507 -0.15 0.880 .9694778 1.026915 | |||||
| hhincome | .9895225 .0086923 -1.20 0.231 .9726318 1.006707 | |||||
| hhsigno | ||||||
| Yes | 1.658753 .1654425 5.07 0.000 1.364217 2.016878 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | 1.181866 .1933766 1.02 0.307 .8576197 1.628702 | |||||
| age | 1.004991 .0194887 0.26 0.797 .967511 1.043924 | |||||
| hhincome | .9717411 .0116616 -2.39 0.017 .9491514 .9948684 | |||||
| hhsigno | ||||||
| Yes | 1.11936 .1454154 0.87 0.385 .8677426 1.443939 | |||||
| Employed | (base outcome) | |||||
Rezultatele sunt similare cu cele ale estimatorului de efecte aleatorii. Și pot fi interpretate în același mod.
