Nouveau dans 
Modèle logit multinomial là données de panel
Le modèle logit multinomial (MNL) est une méthode populaire pour modéliser les résultats catégoriques qui n’ont pas d’ordre naturel – des résultats tels que la profession, le parti politique ou le choix de restaurant.
Dans les données longitudinales/panel, nous observons une séquence de résultats dans le temps. Supposons que nous observions les choix de restaurant effectués par les individus chaque semaine. Pensez-vous que les choix de restaurant sont indépendants d’une semaine à l’autre ? Probablement pas. Une personne qui aime la cuisine italienne est susceptible de choisir un restaurant italien plusieurs fois. Ces choix sont déterminés par des préférences et des caractéristiques personnelles sous-jacentes, dont certaines ne sont pas observées.
La nouvelle commande xtmlogit de Stata ajuste des modèles MNL à effets aléatoires et à effets fixes conditionnels pour des résultats catégoriels observés dans le temps.
Pour ajuster un modèle logit multinomial à effets aléatoires, nous pouvons taper
. xtset subject . xtmlogit restaurant age
et d’estimer les coefficients logit multinomiaux standard tenant compte des caractéristiques spécifiques au sujet et invariables dans le temps en incluant des effets aléatoires spécifiques à chaque niveau de résultat.
Avec la commande ci-dessus, les effets aléatoires sont supposés être normalement distribués et indépendants entre les niveaux de résultats (choix de restaurants), mais plusieurs structures de variance-covariance sont supportées, y compris une covariance complètement libre :
. xtmlogit restaurant age, covariance(unstructured)
Si vous pensez que les effets spécifiques au sujet peuvent être corrélés avec l’âge, vous pouvez utiliser un estimateur conditionnel à effets fixes pour en tenir compte:
. xtmlogit restaurant age, fe
Points forts
Modélisation par panel de données de résultats catégoriques non ordonnés
Estimateur à effets aléatoires
- Choix de la structure de covariance pour les effets aléatoires
- Indépendant
- Identique
- Partagé
- Échangeable
- Non structurée
Estimateur conditionnel à effets fixes (FE)
- Les sous-ensembles de permutation atténuent le fléau de la dimensionnalité.
Estimation bayésienne
Erreurs standard robustes, en grappes et bootstrap
Prise en charge des données d’enquête complexes
Voyons comment cela fonctionne
Nous souhaitons déterminer si les individus sont plus susceptibles d’être en dehors de la population active s’ils ont des enfants de moins de cinq ans dans leur ménage. Nous utiliserons un ensemble de données (fictives) d’hommes et de femmes qui ont été interrogés sur leur situation professionnelle tous les deux ans.
. use https://www.stata-press.com/data/r17/estatus (Fictitious employment status data)
Voici un extrait de l’ensemble de données, montrant l’historique d’emploi de trois personnes :
. list id year estatus hhchild age in 22/41, sepby(id) noobs
| id year estatus hhchild age | ||
| 5 2002 Employed Yes 38 | ||
| 5 2004 Employed No 40 | ||
| 5 2006 Employed No 42 | ||
| 5 2008 Employed No 44 | ||
| 5 2010 Out of labor force No 46 | ||
| 5 2012 Out of labor force No 48 | ||
| 5 2014 Unemployed No 50 | ||
| 6 2002 Unemployed Yes 31 | ||
| 6 2004 Employed Yes 33 | ||
| 6 2006 Out of labor force Yes 35 | ||
| 6 2008 Unemployed Yes 37 | ||
| 6 2010 Out of labor force Yes 39 | ||
| 6 2012 Unemployed No 41 | ||
| 7 2002 Out of labor force Yes 33 | ||
| 7 2004 Employed Yes 35 | ||
| 7 2006 Employed Yes 37 | ||
| 7 2008 Out of labor force Yes 39 | ||
| 7 2010 Employed No 41 | ||
| 7 2012 Employed No 43 | ||
| 7 2014 Employed No 45 | ||
Le résultat qui nous intéresse est le statut d’emploi (estatus), qui comporte trois niveaux : Employé, Chômeur (mais à la recherche d’un emploi), et Hors de la population active (ne cherche pas d’emploi). Notre prédicteur d’intérêt, hhchild, indique s’il y a des enfants de moins de cinq ans dans le ménage au moment de l’interview.
Avant de pouvoir ajuster notre modèle, nous devons spécifier notre variable d’identification du panel, id, en utilisant xtset.
. xtset id Panel variable: id (unbalanced)
Nous pouvons maintenant utiliser xtmlogit pour modéliser la probabilité de chaque type d’emploi par hhchild tout en contrôlant les effets de l’âge, du revenu annuel du ménage (hhincome) et de la présence d’un autre membre significatif dans le ménage (hhsigno). Nous commencerons par un modèle à effets aléatoires (par défaut) et utiliserons l’option rrr pour obtenir des coefficients exponentiels qui peuvent être interprétés comme des ratios de risque relatif.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, rrr
Fitting comparison model ...
Refining starting values:
Grid node 0: log likelihood = -4504.5591
Grid node 1: log likelihood = -4538.6352
Fitting full model:
Iteration 0: log likelihood = -4504.5591
Iteration 1: log likelihood = -4495.871
Iteration 2: log likelihood = -4490.5098
Iteration 3: log likelihood = -4490.4197
Iteration 4: log likelihood = -4490.4196
Random-effects multinomial logistic regression Number of obs = 4,761
Group variable: id Number of groups = 800
Random effects u_i ~ Gaussian Obs per group:
min = 5
avg = 6.0
max = 7
Integration method: mvaghermite Integration pts. = 7
Wald chi2(8) = 199.25
Log likelihood = -4490.4196 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.579937 .1513905 4.77 0.000 1.309414 1.906349 | |||||
| age | .9947946 .0065832 -0.79 0.430 .981975 1.007781 | |||||
| hhincome | .9954927 .0018251 -2.46 0.014 .9919221 .9990762 | |||||
| hhsigno | ||||||
| Yes | 1.642859 .1550291 5.26 0.000 1.365452 1.976625 | |||||
| _cons | .4949307 .1392991 -2.50 0.012 .2850836 .859244 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | .9607243 .1148148 -0.34 0.737 .7601038 1.214296 | |||||
| age | 1.004257 .008211 0.52 0.603 .9882918 1.02048 | |||||
| hhincome | .9696874 .0025722 -11.60 0.000 .964659 .9747421 | |||||
| hhsigno | ||||||
| Yes | 1.099323 .1310654 0.79 0.427 .8702452 1.388701 | |||||
| _cons | .8078165 .280628 -0.61 0.539 .4088963 1.595924 | |||||
| Employed | (base outcome) | |||||
| var(u1) | .8573133 .1083915 .6691459 1.098394 | |||||
| var(u2) | .7378532 .1388652 .5102376 1.067008 | |||||
Les deux premières sections du résultat montrent les estimations du ratio de risque relatif de nos prédicteurs par rapport à la catégorie de base Employé. La dernière section montre les variances estimées des effets aléatoires. Par défaut, les effets aléatoires ne sont pas corrélés, mais leur structure de covariance peut être modifiée en utilisant l’option covariance(). Par exemple, les corrélations entre les effets aléatoires peuvent être estimées en utilisant covariance(unstructured), ou chaque catégorie peut partager un effet aléatoire commun en utilisant covariance(shared).
Après ajustement pour l’âge, le revenu du ménage et le fait d’avoir une personne significative à la maison, le risque relatif d’être en dehors de la population active pour les individus ayant au moins un enfant de moins de 5 ans dans le ménage par rapport à ceux n’ayant aucun enfant de moins de 5 ans dans le ménage est 1,6 fois plus important que le risque relatif d’emploi (IC 95% [1,3, 1,9]). Pour comprendre ces effets en termes de probabilités, nous pouvons utiliser la commande margins.
. margins hhchild Predictive margins Number of obs = 4,761 Model VCE: OIM 1._predict: Pr(estatus==Out_of_labor_force), predict(pr outcome(1)) 2._predict: Pr(estatus==Unemployed), predict(pr outcome(2)) 3._predict: Pr(estatus==Employed), predict(pr outcome(3))
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#hhchild | ||||||
| 1#No | .3025675 .0131546 23.00 0.000 .276785 .32835 | |||||
| 1#Yes | .3912476 .0120405 32.49 0.000 .3676486 .4148466 | |||||
| 2#No | .1628713 .0101131 16.11 0.000 .1430501 .1826925 | |||||
| 2#Yes | .1398537 .0079462 17.60 0.000 .1242794 .1554279 | |||||
| 3#No | .5345612 .0136994 39.02 0.000 .5077108 .5614116 | |||||
| 3#Yes | .4688987 .0116594 40.22 0.000 .4460468 .4917507 | |||||
Pour un individu sans enfant, la probabilité attendue d’être en dehors de la population active (étiqueté 1#No) est de 0,30, la probabilité attendue d’être au chômage (2#No) est de 0,16, et la probabilité attendue d’être employé est de 0,53 (3#No). Nous constatons également que les personnes ayant des enfants dans le ménage augmentent de 9 points de pourcentage leur probabilité de ne pas faire partie de la population active. Nous pourrions voir comment ces probabilités changent en fonction du revenu du ménage en utilisant une commande supplémentaire margins et visualiser les résultats en utilisant marginsplot.
. quietly margins hhchild, at(hhincome=(20(20)100))
. marginsplot, by(_predict, label("Out of labor force" "Unemployed" "Employed"))
byopts(rows(1) title("Marginal probabilities of employment status"))
legend(order(4 "Child under 5 at home" 3 "No child under 5 at home"))
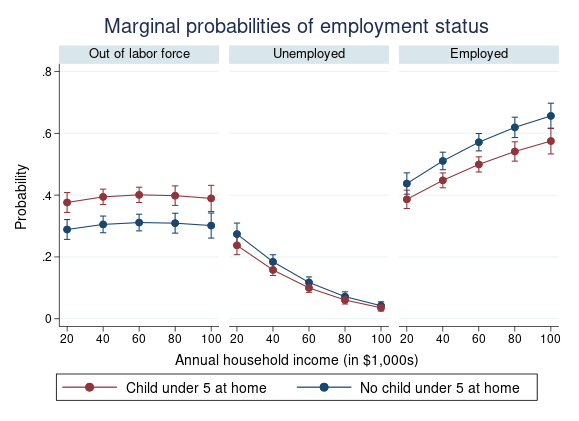
Pour obtenir des graphiques séparés pour chaque résultat, nous avons utilisé l’option by(_predict) dans marginsplot. Le reste des options ajoute des titres et des étiquettes.
En comparant les lignes au sein de chaque catégorie d’emploi, nous voyons que le fait d’avoir un enfant à la maison n’a pas beaucoup d’impact sur la probabilité d’être au chômage, mais influence la décision de travailler ou d’être en dehors de la population active.
Dans le modèle que nous venons d’ajuster, nous avons utilisé des effets aléatoires pour tenir compte des caractéristiques non observées des individus de notre ensemble de données. Les modèles à effets aléatoires exigent que les effets aléatoires soient non corrélés avec les prédicteurs, et le modèle MNL à effets aléatoires ne fait pas exception. Une alternative largement utilisée est l’estimateur à effets fixes. Pour ajuster notre modèle avec des effets fixes conditionnels, nous ajoutons simplement l’option fe.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, fe rrr
note: 80 groups (451 obs) omitted because of no variation in the outcome variable over time.
Computing initial values ...
Setting up 26,168 permutations:
....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%
Fitting full model:
Iteration 0: log likelihood = -2154.4175
Iteration 1: log likelihood = -2154.2058
Iteration 2: log likelihood = -2154.2057
Fixed-effects multinomial logistic regression Number of obs = 4,310
Group variable: id Number of groups = 720
Obs per group:
min = 5
avg = 6.0
max = 7
LR chi2(8) = 67.42
Log likelihood = -2154.2057 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.784236 .2237128 4.62 0.000 1.395488 2.28128 | |||||
| age | .9977834 .0146507 -0.15 0.880 .9694778 1.026915 | |||||
| hhincome | .9895225 .0086923 -1.20 0.231 .9726318 1.006707 | |||||
| hhsigno | ||||||
| Yes | 1.658753 .1654425 5.07 0.000 1.364217 2.016878 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | 1.181866 .1933766 1.02 0.307 .8576197 1.628702 | |||||
| age | 1.004991 .0194887 0.26 0.797 .967511 1.043924 | |||||
| hhincome | .9717411 .0116616 -2.39 0.017 .9491514 .9948684 | |||||
| hhsigno | ||||||
| Yes | 1.11936 .1454154 0.87 0.385 .8677426 1.443939 | |||||
| Employed | (base outcome) | |||||
Les résultats sont similaires à ceux de l’estimateur à effets aléatoires. Et ils peuvent être interprétés de la même
