Újdonságok a  -ben
-ben
Panel-adat multinomiális logit modell
A multinomiális logit (MNL) modell népszerű módszer olyan kategorikus eredmények modellezésére, amelyeknek nincs természetes rendezése – olyan eredmények, mint a foglalkozás, a politikai párt vagy az éttermi választás.
A longitudinális / panel adatokban az eredmények időbeli sorrendjét figyeljük meg. Tegyük fel, hogy minden héten megfigyeljük az egyének által választott éttermi választásokat. Ön szerint az éttermi választás hétről hétre független? Valószinűleg nem. Aki szereti az olasz ételeket, valószínűleg többször választ olasz éttermet. Ezeket a döntéseket a mögöttes személyes preferenciák és jellemzők vezérlik, amelyek némelyikét nem figyelik meg.
A Stata új xtmlogit parancsa véletlenszerű és feltételes fix hatású MNL modellekkel illeszkedik az idővel megfigyelt kategorikus eredményekhez.
Véletlenszerű hatású többnemű logit modell beillesztéséhez beírhatjuk
. xtset subject . xtmlogit restaurant age
és becsülje meg a standard multinomiális logit koefficienseket, amelyek figyelembe veszik az időinvariáns szubjektum-specifikus jellemzőket az egyes kimeneti szintekre jellemző véletlen hatások bevonásával. A fenti paranccsal feltételezzük, hogy a véletlenszerű hatások normálisan eloszlottak és függetlenek az eredmény szintjein (éttermi választások), de számos variancia-kovariancia struktúra támogatott, köztük egy teljesen korlátlan kovariancia:
. xtmlogit restaurant age, covariance(unstructured)
Ha arra gyanakszik, hogy az alanyspecifikus hatások összefüggésben lehetnek az életkorral, akkor ennek feltételezéséhez használjon feltételes rögzített hatású becslést:
. xtmlogit restaurant age, fe
Kiemelt
Rendezetlen kategorikus eredmények paneladat-modellezése
Véletlenszerű hatás becslő
- A kovariancia struktúrájának megválasztása a véletlenszerű effektusokhoz
- Független
- Identitás
- Megosztott
- Cserélhető
- Strukturálatlan
Feltételes fix hatású (FE) becslő
- A permetáció a halmazállapotban csökkenti a dimenzió átkát
Bayesi becslés
Robusztus, klaszter – robusztus és bootstrap szabványos hibák
Komplex felmérési adatok támogatása
Lássuk hogyan mükődik
Szeretnénk megtudni, hogy az egyének nagyobb valószínűséggel vannak-e munkaerő nélkül, ha háztartásukban öt évnél fiatalabb gyermekek vannak. Egy olyan (fiktív) adatkészletet fogunk használni azokról a férfiakról és nőkről, akiket kétévente kérdeztek a foglalkoztatási helyzetükről.
. use https://www.stata-press.com/data/r17/estatus (Fictitious employment status data)
Íme egy részlet az adatkészletből, amely három személy foglalkoztatási történetét mutatja be:
. list id year estatus hhchild age in 22/41, sepby(id) noobs
| id year estatus hhchild age | ||
| 5 2002 Employed Yes 38 | ||
| 5 2004 Employed No 40 | ||
| 5 2006 Employed No 42 | ||
| 5 2008 Employed No 44 | ||
| 5 2010 Out of labor force No 46 | ||
| 5 2012 Out of labor force No 48 | ||
| 5 2014 Unemployed No 50 | ||
| 6 2002 Unemployed Yes 31 | ||
| 6 2004 Employed Yes 33 | ||
| 6 2006 Out of labor force Yes 35 | ||
| 6 2008 Unemployed Yes 37 | ||
| 6 2010 Out of labor force Yes 39 | ||
| 6 2012 Unemployed No 41 | ||
| 7 2002 Out of labor force Yes 33 | ||
| 7 2004 Employed Yes 35 | ||
| 7 2006 Employed Yes 37 | ||
| 7 2008 Out of labor force Yes 39 | ||
| 7 2010 Employed No 41 | ||
| 7 2012 Employed No 43 | ||
| 7 2014 Employed No 45 | ||
Az érdeklődés eredménye a foglalkoztatási státus (estatus), amelynek három szintje van: Employed, Unemployed (de munkát keres) és Out of labor force (nem keres munkát). Érdeklődésünk előrejelzője, hhchild, jelzi, hogy az interjú idején háztartásukban vannak-e öt évnél fiatalabb gyermekek.
Mielőtt illesztenénk a modellünket, meg kell adnunk a panel azonosító változónkat, az id-t az xtset használatával.
. xtset id Panel variable: id (unbalanced)
Most az xtmlogit segítségével modellezhetjük az egyes foglalkoztatási típusok valószínűségét hhchild által, miközben ellenőrizzük az életkor age, , az éves háztartási jövedelem (hhincome), hatásait, és azt, hogy élt-e még egy jelentős másik is a háztartásban (hhsigno). Először egy véletlen-effektus modellel kezdünk (az alapértelmezett), és az rrr opcióval olyan hatványozott együtthatókat kapunk, amelyek relatív kockázat arányként értelmezhetők.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, rrr
Fitting comparison model ...
Refining starting values:
Grid node 0: log likelihood = -4504.5591
Grid node 1: log likelihood = -4538.6352
Fitting full model:
Iteration 0: log likelihood = -4504.5591
Iteration 1: log likelihood = -4495.871
Iteration 2: log likelihood = -4490.5098
Iteration 3: log likelihood = -4490.4197
Iteration 4: log likelihood = -4490.4196
Random-effects multinomial logistic regression Number of obs = 4,761
Group variable: id Number of groups = 800
Random effects u_i ~ Gaussian Obs per group:
min = 5
avg = 6.0
max = 7
Integration method: mvaghermite Integration pts. = 7
Wald chi2(8) = 199.25
Log likelihood = -4490.4196 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.579937 .1513905 4.77 0.000 1.309414 1.906349 | |||||
| age | .9947946 .0065832 -0.79 0.430 .981975 1.007781 | |||||
| hhincome | .9954927 .0018251 -2.46 0.014 .9919221 .9990762 | |||||
| hhsigno | ||||||
| Yes | 1.642859 .1550291 5.26 0.000 1.365452 1.976625 | |||||
| _cons | .4949307 .1392991 -2.50 0.012 .2850836 .859244 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | .9607243 .1148148 -0.34 0.737 .7601038 1.214296 | |||||
| age | 1.004257 .008211 0.52 0.603 .9882918 1.02048 | |||||
| hhincome | .9696874 .0025722 -11.60 0.000 .964659 .9747421 | |||||
| hhsigno | ||||||
| Yes | 1.099323 .1310654 0.79 0.427 .8702452 1.388701 | |||||
| _cons | .8078165 .280628 -0.61 0.539 .4088963 1.595924 | |||||
| Employed | (base outcome) | |||||
| var(u1) | .8573133 .1083915 .6691459 1.098394 | |||||
| var(u2) | .7378532 .1388652 .5102376 1.067008 | |||||
A kimenet első két szakasza bemutatja előrejelzőink relatív kockázat arányát az alapkategóriához képest Employed. Az utolsó szakasz a véletlenszerű hatások becsült eltéréseit mutatja be. Alapértelmezés szerint a véletlenszerű effektusok nincsenek korrelálva, de a kovariancia szerkezetük a covariance() opcióval megváltoztatható. Például a véletlenszerű hatások közötti összefüggések megbecsülhetők a covariance(unstructured), használatával, vagy mindegyik kategória megoszthatja a közös véletlenszerű hatást a covariance(shared) használatával.
Az életkor, a háztartás jövedelme és az otthonában jelentős más személyek arányos kiigazítása esetén a relatív kockázat, hogy kimarad a munkaerőből azoknak az egyéneknek, akiknek legalább egy 5 évesnél fiatalabb gyermeke van a háztartásban, szemben azzal, hogy nincsenek háztartásban 5 év alatti gyermekek 1,6-szor akkora, mint a foglalkoztatás relatív kockázata (95% CI [1,3, 1,9]). Ezeknek a hatásoknak a valószínûség szempontjából való megértéséhez használhatjuk a margins parancsot.
. margins hhchild Predictive margins Number of obs = 4,761 Model VCE: OIM 1._predict: Pr(estatus==Out_of_labor_force), predict(pr outcome(1)) 2._predict: Pr(estatus==Unemployed), predict(pr outcome(2)) 3._predict: Pr(estatus==Employed), predict(pr outcome(3))
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#hhchild | ||||||
| 1#No | .3025675 .0131546 23.00 0.000 .276785 .32835 | |||||
| 1#Yes | .3912476 .0120405 32.49 0.000 .3676486 .4148466 | |||||
| 2#No | .1628713 .0101131 16.11 0.000 .1430501 .1826925 | |||||
| 2#Yes | .1398537 .0079462 17.60 0.000 .1242794 .1554279 | |||||
| 3#No | .5345612 .0136994 39.02 0.000 .5077108 .5614116 | |||||
| 3#Yes | .4688987 .0116594 40.22 0.000 .4460468 .4917507 | |||||
Gyermek nélküli egyén esetében a munkaerőből való kilépés várható valószínűsége (labeled 1#No) 0,30, a munkanélküliség várható valószínűsége (2#No) 0,16, az alkalmazás várható valószínűsége pedig 0,53 (3#No). Azt is tapasztaltuk, hogy a háztartásban gyermekes egyének 9 százalékponttal növelik annak esélyét, hogy munkaerő nélkül maradjanak. Láthattuk, hogy ezek a valószínűségek hogyan változnak a háztartások jövedelme szerint egy további margók paranccsal, és az eredményeket a marginsplot segítségével jeleníthetjük meg
We could see how these probabilities change by household income using an additionalLáthattuk, hogy ezek a valószínűségek hogyan változnak a háztartások jövedelme szerint egy további margins paranccsal, és az eredményeket a marginsplot segítségével jeleníthetjük meg.
. quietly margins hhchild, at(hhincome=(20(20)100))
. marginsplot, by(_predict, label("Out of labor force" "Unemployed" "Employed"))
byopts(rows(1) title("Marginal probabilities of employment status"))
legend(order(4 "Child under 5 at home" 3 "No child under 5 at home"))
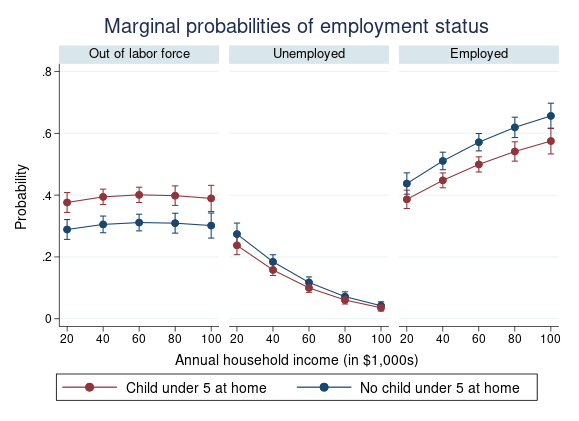
Az egyes eredményekhez külön grafikonok készítéséhez a marginsplot ban a (_predict) opciót használtuk. A többi lehetőség címet és címkét ad hozzá.
Az egyes foglalkoztatási kategóriákon belüli vonalak összehasonlításával azt látjuk, hogy az otthoni gyermekvállalás nincs sok hatással a munkanélküliség valószínűségére, de befolyásolja a munkavállalás vagy a munkaerőből való kilépés döntését.
Az éppen illeszkedő modellben véletlenszerű effektusokkal vettük figyelembe az adatkészletünkben az egyének megfigyelhetetlen jellemzőit. A véletlen hatású modellek megkövetelik, hogy a véletlen hatások ne legyenek korrelálva a prediktorokkal, és a véletlen hatású MNL modell sem kivétel. Széles körben használt alternatíva a fix hatás becslője. Ahhoz, hogy modellünk feltételesen rögzített effektekkel illeszkedjen, egyszerűen hozzáadjuk a fe opciót.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, fe rrr
note: 80 groups (451 obs) omitted because of no variation in the outcome variable over time.
Computing initial values ...
Setting up 26,168 permutations:
....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%
Fitting full model:
Iteration 0: log likelihood = -2154.4175
Iteration 1: log likelihood = -2154.2058
Iteration 2: log likelihood = -2154.2057
Fixed-effects multinomial logistic regression Number of obs = 4,310
Group variable: id Number of groups = 720
Obs per group:
min = 5
avg = 6.0
max = 7
LR chi2(8) = 67.42
Log likelihood = -2154.2057 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.784236 .2237128 4.62 0.000 1.395488 2.28128 | |||||
| age | .9977834 .0146507 -0.15 0.880 .9694778 1.026915 | |||||
| hhincome | .9895225 .0086923 -1.20 0.231 .9726318 1.006707 | |||||
| hhsigno | ||||||
| Yes | 1.658753 .1654425 5.07 0.000 1.364217 2.016878 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | 1.181866 .1933766 1.02 0.307 .8576197 1.628702 | |||||
| age | 1.004991 .0194887 0.26 0.797 .967511 1.043924 | |||||
| hhincome | .9717411 .0116616 -2.39 0.017 .9491514 .9948684 | |||||
| hhsigno | ||||||
| Yes | 1.11936 .1454154 0.87 0.385 .8677426 1.443939 | |||||
| Employed | (base outcome) | |||||
Az eredmények hasonlóak a véletlenszerű hatások becslőjéhez. És ugyanúgy értelmezhetők.
