Ez egy jelentős kiadás

A 14.2-es verzió idén január 23-án jelent meg. Most, mindössze hat hónappal később, megérkezik a 14.3-as verzió. Bár a verziószám .x jelölése szerénynek tűnhet, valójában ez egy jelentős kiadás, számos fontos, új és frissített funkcióval, különösen a rendszer alapvető területein.

Különösen örömmel jelenthetem be, hogy ebben a kiadásban rendkívül sok, régóta várt funkciót valósítottunk meg. Miért nem érkeztek ezek korábban? Nos, nehéz volt megvalósítani őket – legalábbis a mi magas minőségi elvárásaink szerint. De most itt vannak, készen arra, hogy mindenki használhassa őket.

Azok, akik követték a nyilvános, élő közvetítésű szoftvertervezési megbeszéléseinket (amelyekből 42 óra telt el a 14.2-es verzió óta), talán érzékelik, mekkora erőfeszítést tettünk a tervezés tökéletesítéséért. Valójában közel négy évtizede, az első 1.0 verzió fejlesztése óta folyamatosan ezt az intenzív munkát végezzük. Az eredmény pedig – úgy gondolom – teljesen egyedülálló a szoftvervilágban: egy olyan rendszer, amely minden tekintetben következetes és koherens, és amely 37 éve megőrizte kompatibilitását.

Ez most már egy nagyon nagy rendszer, és még én is néha megfeledkezem egyes csodálatos képességeiről. Azonban ami manapság rendszeresen segít nekem ebben, az a tavaly év végén megjelent Jegyzetfüzet Asszisztens (Notebook Assistant). Ha valamit ki akarok próbálni, csak beírok egy laza leírást arról, amit szeretnék a Jegyzetfüzet Asszisztensbe. Ez az asszisztens aztán meglepően jól „élesíti” a kérésemet, és releváns Wolfram Language kódokat generál.

Gyakran túl általános voltam, így a kód nem mindig pontosan az volt, amit szerettem volna. De majdnem mindig a megfelelő irányba terelt, és kisebb módosításokkal pontosan azt a megoldást adta, amire szükségem volt.

Ez egy nagyon jó munkafolyamat, amely az AI legújabb vívmányainak és a Wolfram Language egyedi jellemzőinek ötvözésével vált lehetővé. Én valamiféle homályos kérdést teszek fel, a Jegyzetfüzet Asszisztens pedig pontos kódot ad. De a legfontosabb, hogy ez a kód nem egyszerű programozási nyelvi kód, hanem a Wolfram Language számítási nyelvi kódja. Olyan kód, amely kifejezetten emberi olvasásra készült, és amely a világot a lehető legmagasabb szinten számítási szempontból reprezentálja. Az AI az őt jellemző heuristikus módon működik. De ha kiválasztod a kívánt Wolfram Language kódot, akkor egy pontos, megbízható alapot kapsz, amelyre építhetsz.

Elképesztő, mennyire fontos a Wolfram Language tervezési következetessége sok szempontból. Ez teszi lehetővé, hogy a nyelv különböző részei ilyen simán működjenek együtt. Ez könnyűvé teszi az új területek elsajátítását is. És manapság az AI-k számára is megkönnyíti a nyelv hatékony használatát – az AI ugyanis eszközként hívja segítségül, hasonlóan, mint az emberek.

A Wolfram Language következetes tervezése és gazdag tartalma egy másik következménnyel is jár: könnyen bővíthető. Az elmúlt hat évben több mint 3200 kiegészítő függvényt tettünk közzé a Wolfram Function Repository-ban. És igen, ezek közül jó néhány idővel teljes értékű beépített funkcióvá válhat – néha akár egy évtized múlva is. De jelenleg a Jegyzetfüzet Asszisztens már ismeri ezeket a funkciókat jelenlegi formájukban, és automatikusan meg tudja mutatni, hol illesztheted be őket a munkádba.

Na de térjünk vissza a 14.3-as verzióhoz, amiről rengeteg újdonságot lehet beszélni…

 

Going Dark: Megérkezik a sötét mód

1976-ban kezdtem el használni képernyős számítógépeket. Akkoriban minden képernyő fekete volt, és a rajta megjelenő szöveg fehér. 1982-ben, amikor megjelentek az úgynevezett „munkaállomás” (workstation) számítógépek, ez megfordult, és olyan kijelzőket kezdtem használni, amelyek inkább a nyomtatott oldalakhoz hasonlítottak: fekete szöveg fehér háttéren. Ez volt az általános működés évtizedeken át. Aztán, nagyjából öt évvel ezelőtt, egyre népszerűbbé vált a „sötét mód” (dark mode) — ami tulajdonképpen visszatért a 1970-es évek stílusához, de már teljes színvilággal, jóval nagyobb felbontással és egyéb fejlesztésekkel. Jegyzetfüzetekben (notebooks) már régóta elérhetők voltak sötét mód stílusok, de a 14.3-as verzióban már teljes körű támogatást kapott a sötét mód. Ha a rendszeredet sötét módra állítod, akkor a 14.3-as verzióban az összes jegyzetfüzet alapértelmezés szerint automatikusan sötét módban fog megjelenni:

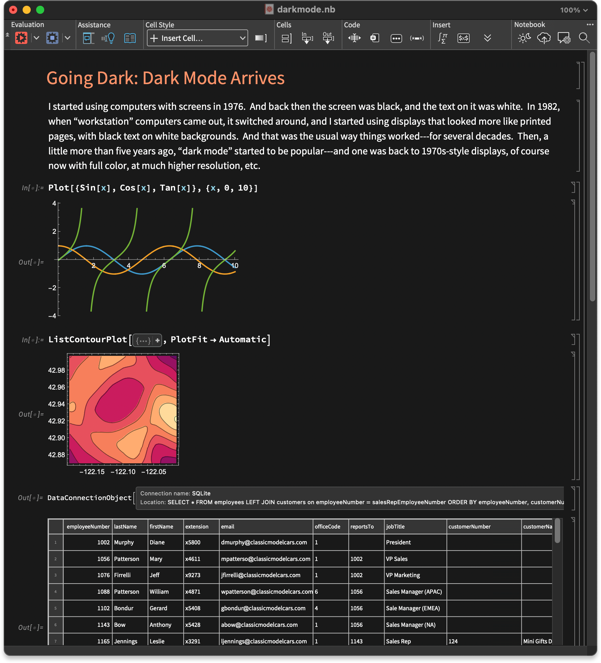
Azt gondolhatnánk: nem egyszerű beállítani a sötét módot? Nem csak annyiból áll, hogy a hátteret feketére, a szöveget pedig fehérre cseréljük? Nos, valójában ennél sokkal, de sokkal több dologról van szó. Végső soron ez egy meglehetősen összetett felhasználói felületbeli és algoritmikus kihívás, amelyet úgy gondolom, a 14.3-as verzióban nagyon szépen sikerült megoldanunk.

Íme egy alapvető kérdés: mi történjen egy diagrammal, amikor átváltunk sötét módra? Szeretnénk, ha a tengelyek fehérré válnának, ugyanakkor a görbék megőriznék a színeiket (hiszen mi történne a szöveggel, amely színek alapján hivatkozik a görbékre?). Pontosan ez történik a 14.3-as verzióban:

 

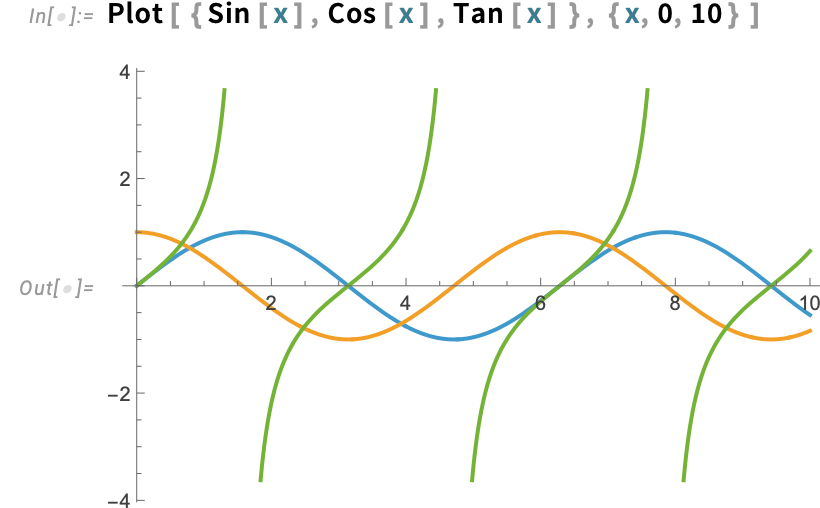
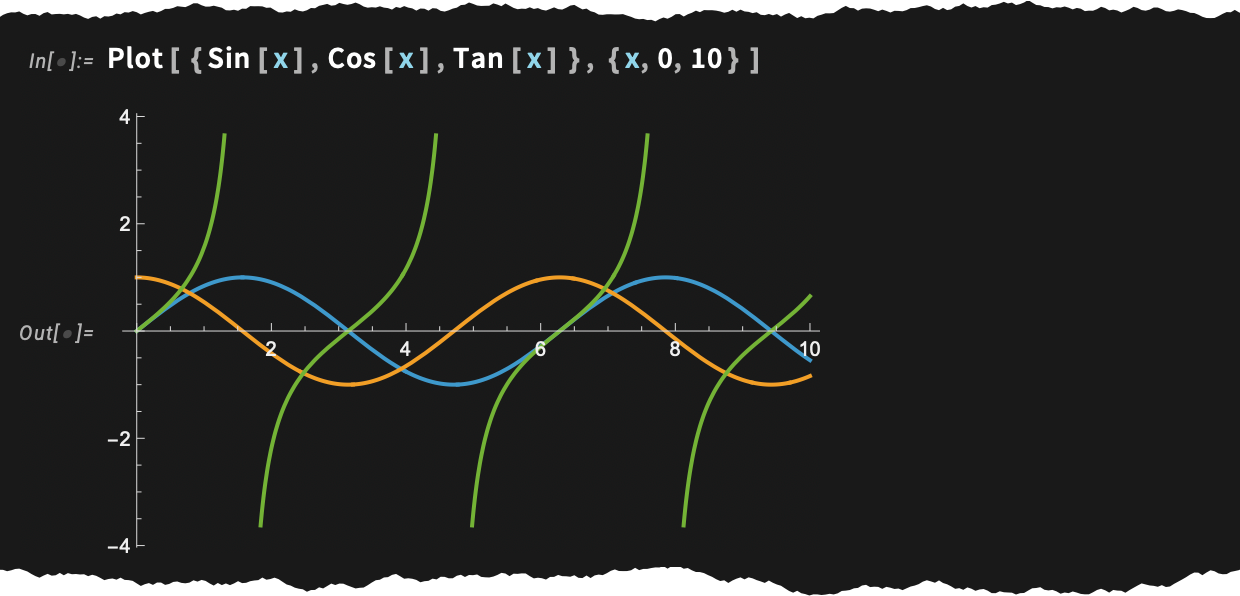
Mondanunk sem kell, az egyik kényes pont az, hogy a görbék színeit úgy kell megválasztani, hogy azok világos és sötét módban egyaránt jól mutassanak. Valójában már a 14.2-es verzióban, amikor „feljavítottuk” az alapértelmezett diagram­színeinket, ezt részben éppen a sötét mód bevezetésére való felkészülés jegyében tettük.

A 14.3-as verzióban (ahogy alább részletesebben is kifejtjük) folytattuk a grafikai színek továbbfejlesztését, számos kényes esetet lefedve, és mindig úgy alakítva a beállításokat, hogy a sötét módot éppúgy támogassák, mint a világos módot:

 

A számítással előállított grafikonok azonban nem az egyetlen elemek, amelyeket érint a sötét mód. Számtalan egyéb felhasználói felületi elem is van, amelyeket mind úgy kell átalakítani, hogy sötét módban is esztétikusan jelenjenek meg. Összességében több ezer szín érintett, amelyeket következetes és ízléses módon kell kezelni. Ennek érdekében végül egy teljes módszer- és algoritmuskészletet dolgoztunk ki (amelyet a jövőben paclet formájában külsőleg is elérhetővé fogunk tenni).

Az eredmény például az, hogy egy jegyzetfüzetet gyakorlatilag automatikusan be lehet állítani úgy, hogy sötét módban működjön:

De mi történik a háttérben? Mondanunk sem kell, hogy ebben egy szimbolikus reprezentáció játszik szerepet. Normál esetben egy színt például így adunk meg: RGBColor[1,0,0]. A 14.3-as verzióban azonban ehelyett használhatunk egy olyan szimbolikus reprezentációt is, mint például:

 

Világos módban ez pirosként fog megjelenni, sötét módban pedig rózsaszínként:

 

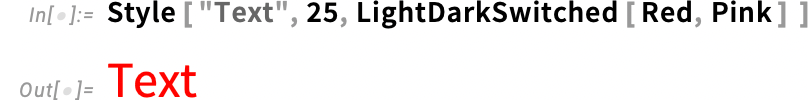
Ha csak egyetlen színt adunk meg a LightDarkSwitched-ben, automatikus algoritmusaink lépnek működésbe, és ebben az esetben sötét módban rózsaszínes színt állítanak elő:

 

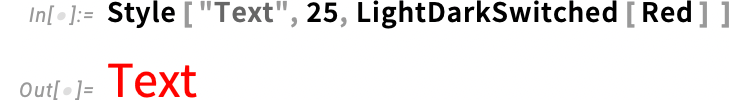
Ez a beállítás meghatározza a sötét mód színét, miközben automatikusan kiszámítja a hozzá megfelelő világos mód színt:

 

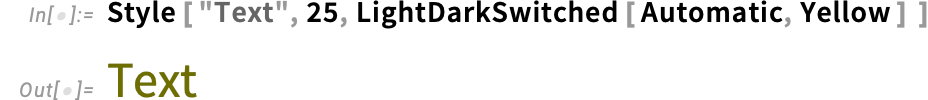
De mi történik, ha nem szeretnénk minden egyes használt szín köré kifejezetten a LightDarkSwitched-et beszúrni? (Például ha már van egy nagy kódbázisunk tele színekkel.) Ilyenkor használhatjuk az új stílusopciót, a LightDarkAutoColorRules-t, amellyel globálisan meghatározhatjuk, hogyan szeretnénk a színek váltását. Például az alábbi beállítás automatikus világos–sötét váltást engedélyez a „felsorolt színekre” (itt csak a Blue-ra), de másokra (pl. Red) nem:

 

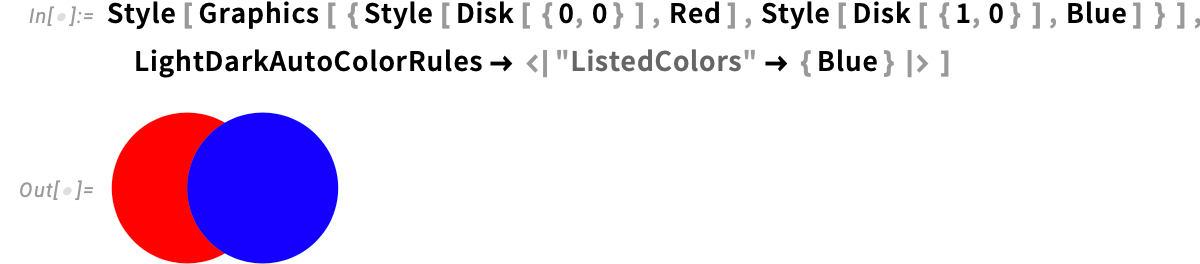
Használhatjuk a LightDarkAutoColorRules All beállítást is, amely az automatikus váltó algoritmusainkat minden színre alkalmazza:

 

Ezen felül ott van a kényelmes LightDarkAutoColorRules -> “NonPlotColors” beállítás is, amely automatikus váltást alkalmaz, de csak azokra a színekre, amelyek nem az alapértelmezett diagramszínek. Ezeket, ahogy fentebb már említettük, úgy alakítottuk ki, hogy mind világos, mind sötét módban változatlanul működjenek.

Mindez számos finomságot rejt magában. Például a 14.3-as verzióban sok függvényt frissítettünk, hogy képesek legyenek világos–sötét váltott színeket előállítani. Ha azonban ezek a színek LightDarkSwitched-et használva tárolódtak egy jegyzetfüzetben, és megpróbáltuk azt egy korábbi verzióval megnyitni, a színek nem jelentek volna meg (és hibajelzéseket kaptunk volna). (Történetesen a LightDarkSwitched-et már a 14.2-es verzióban csendben bevezettük, de korábbi verziókban ez nem működött.)

Hogyan oldottuk meg tehát a visszamenőleges kompatibilitást a függvényeink által előállított világos–sötét váltott színek esetén? Valójában nem tároljuk ezeket a színeket LightDarkSwitched formátumban a jegyzetfüzet kifejezéseiben. Ehelyett a színeket hagyományos RGBColor formában tároljuk, de az r, g, b értékek magasabb helyi számjegyeiben szteganografikusan kódolva tartalmazzák a „váltott” változatukat. A korábbi verziók ezt egyszerű színként olvasták be, amely szinte észrevétlenül eltért a megszokottól; a 14.3-as verzió viszont ezt már világos–sötét váltott színként kezeli.

Nagyon sok erőfeszítést tettünk, hogy a sötét mód megfelelően működjön a jegyzetfüzeteinkben. Az operációs rendszereknek azonban szintén van lehetőségük a sötét mód kezelésére, és néha egyszerűen azt szeretnénk, ha a színek követnék az operációs rendszer beállításait. A 14.3-as verzióban ehhez bevezettük a SystemColor opciót. Például az alábbi beállítással azt mondjuk, hogy egy keret belsejében a háttér kövesse — világos és sötét módban egyaránt — az operációs rendszer által a felugró tippekhez (tooltip) használt színt:

 

Egy dolgot eddig még nem említettünk kifejezetten: hogyan kezeljük a jegyzetfüzetek szöveges tartalmát sötét módban. A fekete szöveget (természetesen) fehérként jelenítjük meg sötét módban. De mi a helyzet a szakaszcímekkel, vagy akár az entitásokkal?

Nos, a világos és sötét módban eltérő színeket használnak. De hogyan használhatod ezeket a színeket a saját programjaidban? A válasz: a ThemeColor segítségével. A ThemeColor-t valójában a 14.2-es verzióban vezettük be, de ez része egy egész keretrendszernek, amelyet folyamatosan bővítünk a következő verziókban. Az elképzelés az, hogy a ThemeColor lehetővé teszi, hogy hozzáférj bizonyos „témákhoz” rendelt „témaszínekhez”. Például léteznek olyan témaszínek, mint az “Accent1” stb., amelyek egy adott kombinációban a “Section” stílus színének meghatározására szolgálnak. A ThemeColor segítségével ezekhez a színekhez is hozzáférhetsz. Például az alábbi szöveg az “Accent3” témaszínnel jelenik meg:

 

És igen, sötét módban automatikusan vált:

 

Rendben, tehát áttekintettük a világos és sötét mód működésének számos részletét. De hogyan dönthetjük el, hogy egy adott jegyzetfüzet világos vagy sötét módban jelenjen meg? Nos, általában erre nincs szükség, mert a váltás automatikusan megtörténik az általános rendszerbeállításoknak megfelelően.

Ha azonban kifejezetten szeretnéd rögzíteni egy jegyzetfüzet esetében a világos vagy sötét módot, ezt megteheted a jegyzetfüzet eszköztárában található gomb segítségével. Programozottan is beállíthatod (vagy a Wolfram System beállításai között) a LightDark opció használatával.

Tehát most már támogatjuk a sötét módot. Vajon 45 évet visszatekerjek magamnak, és a munkám nagy részét — amelyet, mondanom sem kell, Wolfram Language-ben végzek — sötét módban folytassam? A Wolfram Notebooks sötét módja annyira jól néz ki, hogy azt hiszem, ezt bizony meg is tehetem…

 

Hogyan kapcsolódik az AI-hez? Kapcsolat az ügynökvilággal

 

Bizonyos szempontból a Wolfram Language egész története az „AI”-ról szól. Arról, hogy a lehető legtöbbet automatizáljuk, így neked, mint felhasználónak, csak annyi a dolgod, hogy „megmondd, mit szeretnél”, és a rendszer rendelkezik egy teljes automatizációs tornyokkal, amelyek végrehajtják azt helyetted. Természetesen a Wolfram Language fő gondolata az, hogy a lehető legjobb módot biztosítsa arra, hogy „megmondd, mit szeretnél” — vagyis a gondolataidat a lehető legformálisabb számítási módon tudd kifejezni, hogy jobban megértsd őket, és a számítógéped is a szükséges mértékben dolgozhasson rajtuk. A modern, „ChatGPT utáni” AI különösen fontos szerepet játszik abban, hogy egy kiterjedtebb „nyelvi felhasználói felületet” biztosítson mindehhez. A Wolfram|Alpha-ban úttörőként vezettük be a természetes nyelvi értelmezést a számítások előfutáraként; a modern nagy nyelvi modellek (LLM-ek) ezt kiterjesztik, lehetővé téve, hogy teljes beszélgetéseket folytass természetes nyelven.

Ahogyan máshol részletesen is kifejtettem, a nagy nyelvi modellek (LLM-ek) erőssége egészen más, mint a Wolfram Language-é. Bizonyos szinten az LLM-ek képesek olyan dolgokra, amire az emberi agy is képes (bár gyakran nagyobb skálán, gyorsabban stb.). Azonban a nyers számítások és a pontos tudás tekintetében az LLM-ek (vagy az agy) nem annyira hatékonyak.

Természetesen van egy nagyon jó megoldás erre: egyszerűen hagyjuk, hogy az LLM a Wolfram Language-t (és a Wolfram|Alpha-t) eszközként használja. Valójában a ChatGPT megjelenését követő néhány hónapon belül már lehetővé tettük, hogy az LLM-ek a technológiánkat eszközként hívhassák. Azóta egyre jobb módszereket dolgozunk ki erre, és hamarosan egy jelentős kiadás is várható ezen a területen.

Manapság népszerű arról beszélni, hogy „AI ügynökök” „csak elmennek és hasznos dolgokat csinálnak”. Bizonyos szinten a Wolfram Language (és a Wolfram|Alpha) úgy is felfogható, mint „univerzális ügynökök”, amelyek képesek a teljes „számítási feladatok” skáláját elvégezni (és rengeteg külső rendszerhez is kapcsolódni a világban). (Igen, a Wolfram Language képes e-mailt küldeni, weboldalakat böngészni — és sok más dolgot „működtetni” a világban — és évtizedek óta képes ezekre.) Ha egy ügynök magját LLM-ekből építjük fel, a Wolfram Language (és a Wolfram|Alpha) „univerzális eszközként” szolgálnak, amelyeket az LLM-ek hívhatnak segítségül.

Tehát bár az LLM-ek és a Wolfram Language nagyon különböző dolgokra képesek, fokozatosan egyre összetettebb módokat dolgoztunk ki arra, hogy kölcsönhatásba léphessenek, és mindkettőből a lehető legjobbat lehessen kihozni. 2023 közepén bevezettük az LLMFunction-t és társait, hogy az LLM-eket a Wolfram Language-en belül hívhassuk. Ezt követően bevezettük az LLMTool-t, amely lehetővé teszi Wolfram Language-es eszközök definiálását, amelyeket az LLM-ek hívhatnak. A 14.3-as verzióban pedig újabb szintet értünk el ebben az integrációban az LLMGraph-szal.

Az LLMGraph célja, hogy lehetővé tegye egy „ügynöki munkafolyamat” közvetlen definiálását a Wolfram Language-ben, egy olyan „tervgráf” megadásával, amelynek csomópontjai LLM-promptokat vagy futtatandó Wolfram Language-kódot adhatnak. Gyakorlatilag az LLMGraph a meglévő LLM-funkcióink általánosítása, további lehetőségekkel, például különböző részek párhuzamos futtatásának támogatásával.

Íme egy nagyon egyszerű példa: egy LLMGraph, amelynek mindössze két csomópontja van, és párhuzamosan végrehajthatók, az egyik egy haikut, a másik pedig egy limericket generál:

 

Ezt alkalmazhatjuk egy adott bemenetre; az eredmény egy asszociáció lesz (amit itt a Dataset segítségével formázunk):

 

Íme egy kicsit bonyolultabb példa: egy munkafolyamat, amely szövegösszefoglalást végez. A szöveget először darabokra bontja egy Wolfram Language-függvény segítségével, majd párhuzamosan futtat LLM-funkciókat a darabok összefoglalására, végül egy másik LLM-funkciót futtat, amely a darabok összefoglalóiból egyetlen összegző szöveget készít:

 

Ez ábrázolja az LLMGraph-unkat:

 

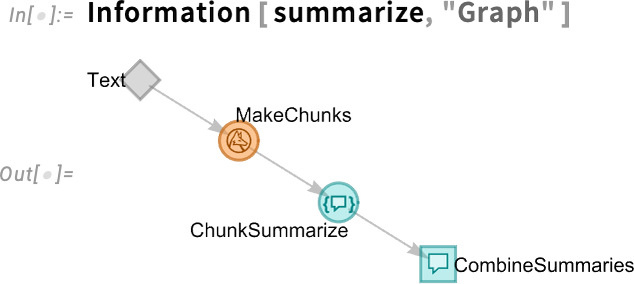
Ha az LLMGraph-unkat alkalmazzuk például az Egyesült Államok alkotmányára, az eredmény egy összegzés lesz:

 

Az LLMGraph-objektumokhoz számos részletes beállítás tartozik. Itt például a “ChunkSummary” esetében a “ListableLLMFunction” kulcsot használtuk, amely azt jelzi, hogy az általunk megadott LLMFunction prompt egy bemeneti lista elemein is végrehajtható (ebben az esetben a Wolfram Language által a “TextChunk”-ban generált darabok listáján).

Az LLMGraph egyik fontos jellemzője a „tesztfüggvények” támogatása: ezek olyan csomópontok a gráfban, amelyek teszteket hajtanak végre, és meghatározzák, hogy egy másik csomópontot szükséges-e futtatni vagy sem. Íme egy kicsit bonyolultabb példa (és igen, az LLM-promptok ilyenkor szükségszerűen kicsit terjedelmesek):

 

 

Ez ábrázolja az LLM-gráfot:

 

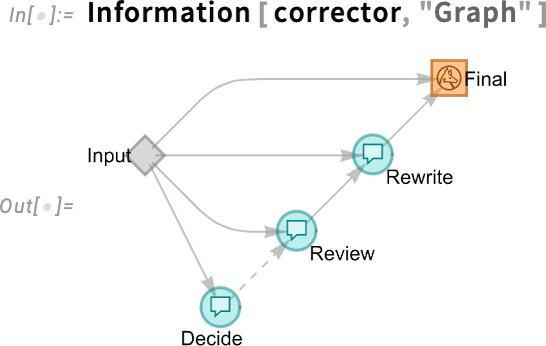
Ha helyes számításon futtatjuk, egyszerűen visszaadja a számítást:

 

Ha azonban helytelen számításon futtatjuk, megpróbálja kijavítani azt, és itt helyesen teszi:

 

Ez egy viszonylag egyszerű példa. De – mint minden a Wolfram Language-ben – az LLMGraph úgy van felépítve, hogy tetszőleges méretekig skálázható legyen. Gyakorlatilag egy új programozási módot kínál – aszinkron feldolgozással kiegészítve – az „ügynöki” LLM világ számára. Ez a Wolfram Language és az AI képességek folyamatos integrációjának része.

 

Csak adj rá egyet!

 

Mondjuk ábrázolsz néhány adatot (és igen, ehhez a 14.2-es verzió új táblázatos adatkezelési képességeit használjuk):

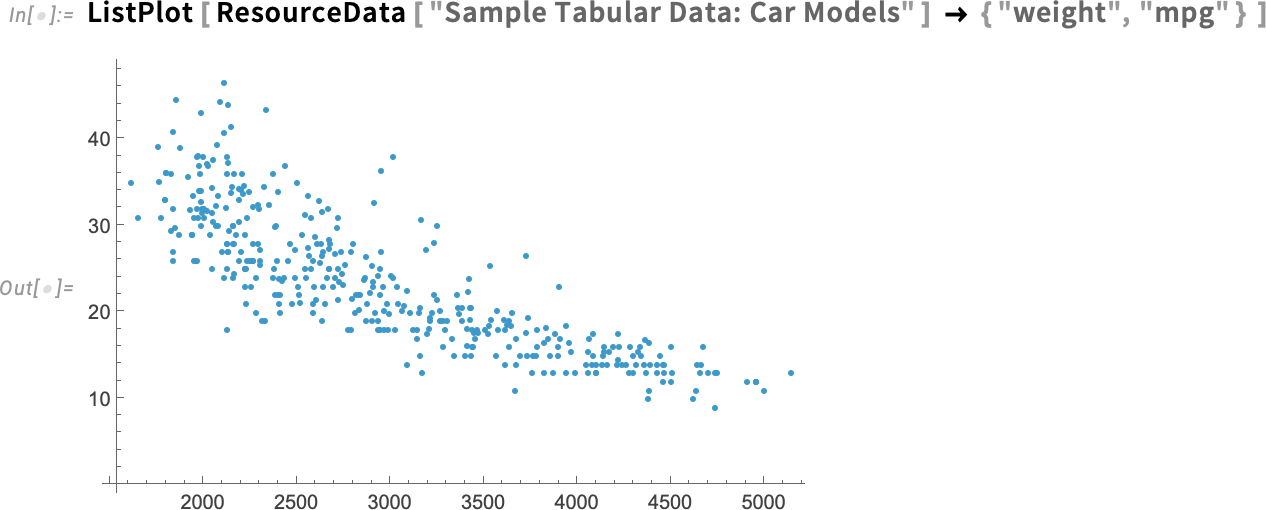
Mi is történik valójában ezekben az adatokban? Mik a trendek? Gyakran az ember valamilyen illesztést próbál készíteni az adatokra, hogy ezt kiderítse. Nos, a 14.3-as verzióban most már van erre egy nagyon egyszerű módszer ListFitPlot:

 

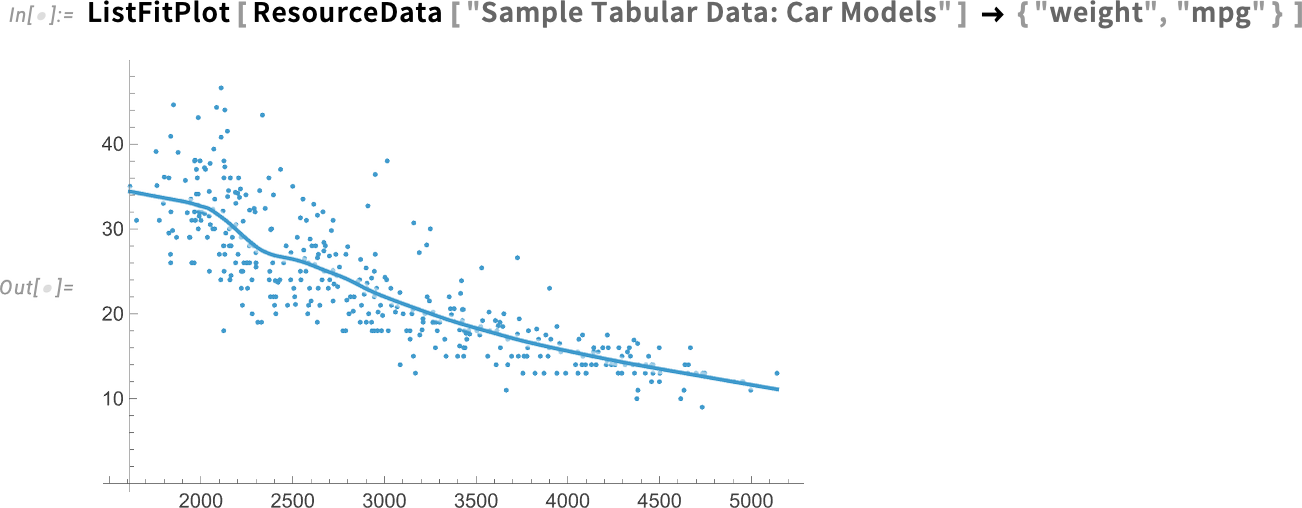
Ez egy lokális illesztés az adatokhoz (ahogy alább meg fogjuk beszélni). De mi van akkor, ha kifejezetten globális lineáris illesztést szeretnénk? Erre is van egy egyszerű opció:

 

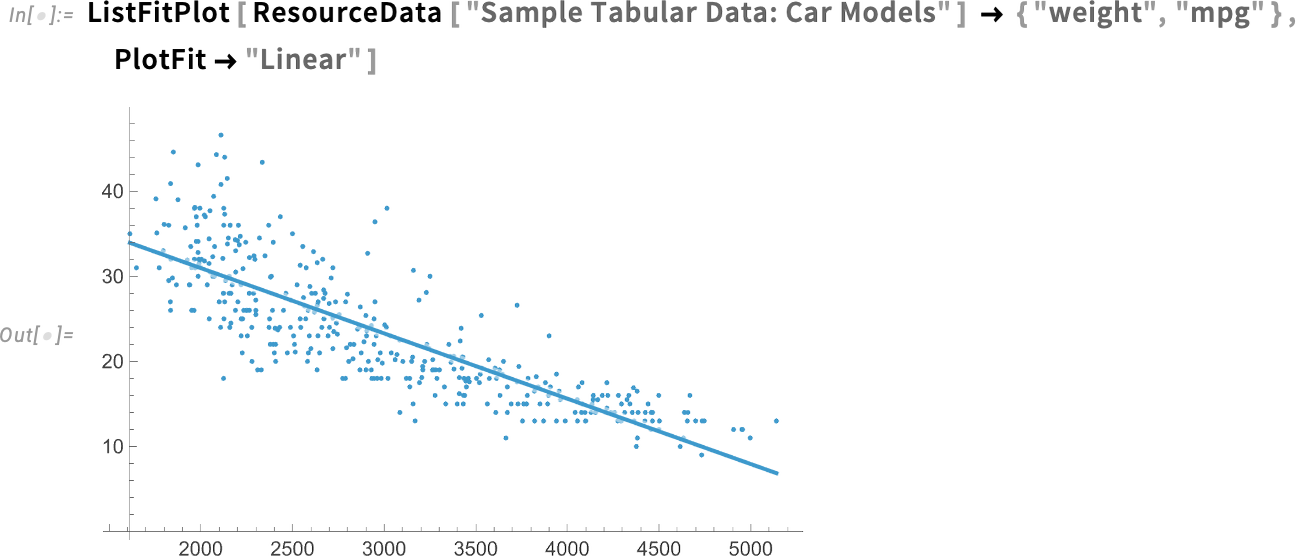
És íme egy exponenciális illesztés:

 

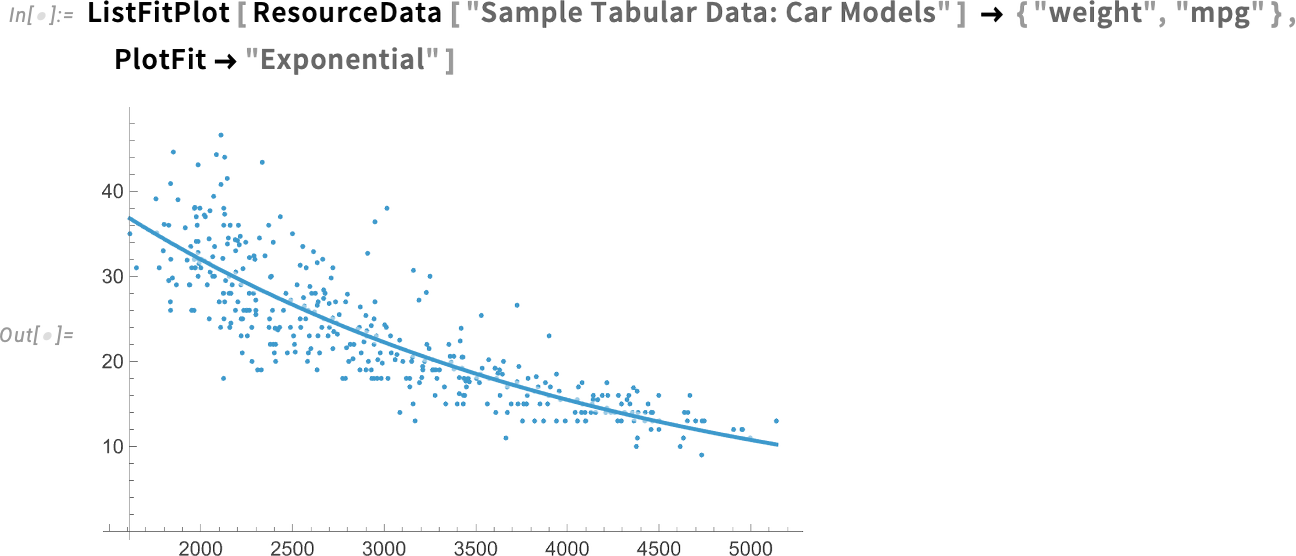
Amit itt ábrázolunk, azok az eredeti adatpontok az illesztéssel együtt. A PlotFitElements opcióval pontosan meg lehet adni, mit ábrázoljunk. Itt például azt mondjuk, hogy (95%-os konfidencia) sávgörbéket is rajzoljon:

 

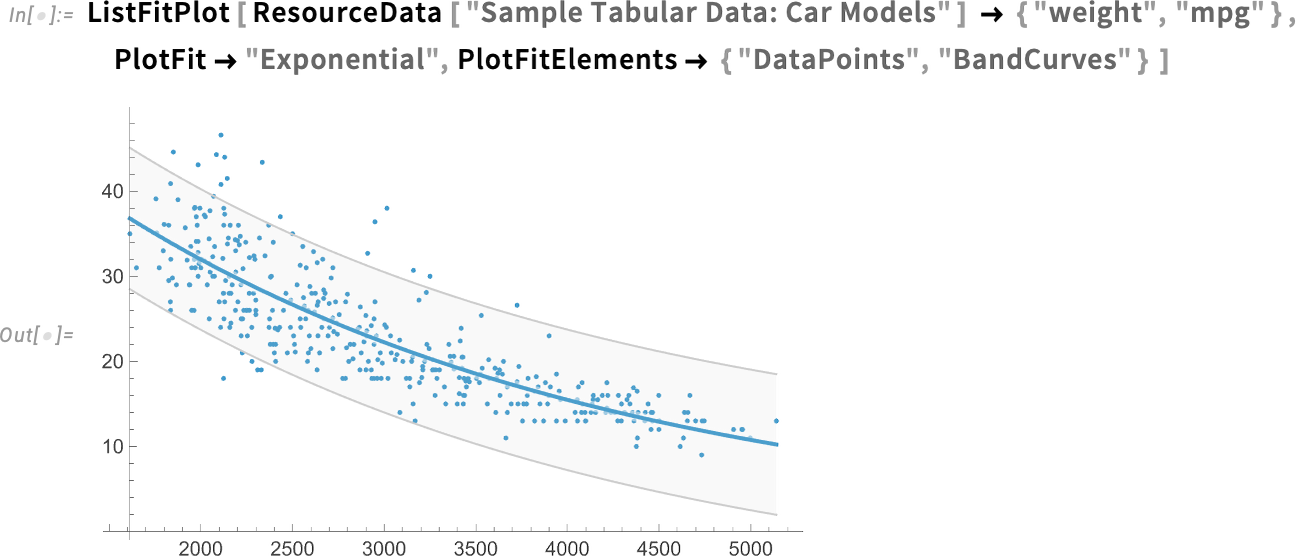
Rendben, tehát így lehet szemléltetni az illesztéseket. De mi a helyzet azzal, ha meg akarjuk tudni, hogy pontosan mi volt az illesztés? Nos, erre már eddig is voltak függvények, mint például a LinearModelFit és a NonlinearModelFit. A 14.3-as verzióban azonban megjelent az új LocalModelFit is:

 

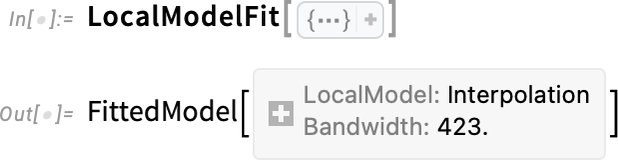
A LinearModelFit stb. függvényekhez hasonlóan ez is egy szimbolikus FittedModel objektumot ad vissza—amit aztán például ábrázolhatunk is:

 

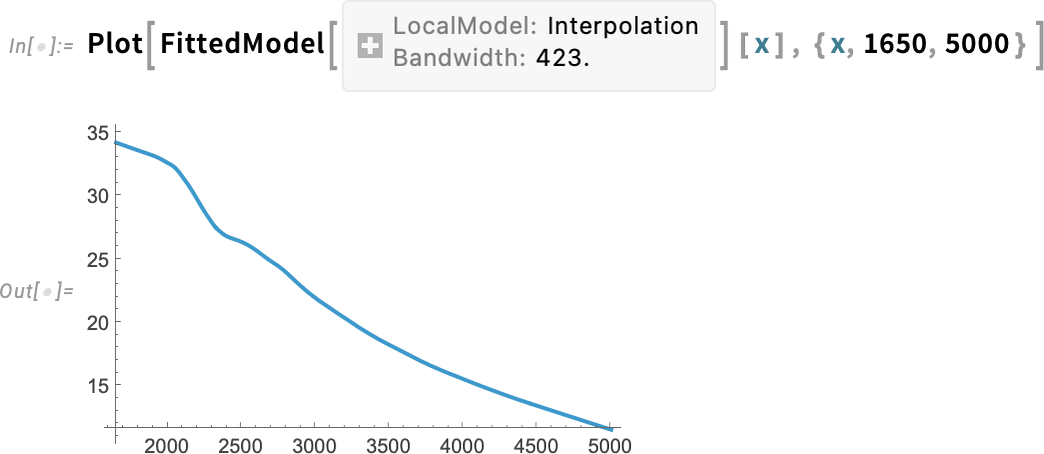
A LocalModelFit egy nemparaméteres illesztési függvény, amely helyi polinomiális regressziókkal (LOESS) működik. A 14.3-as verzió egy másik új függvénye a KernelModelFit, amely bázisfüggvény-magok összegéhez illeszt.

 

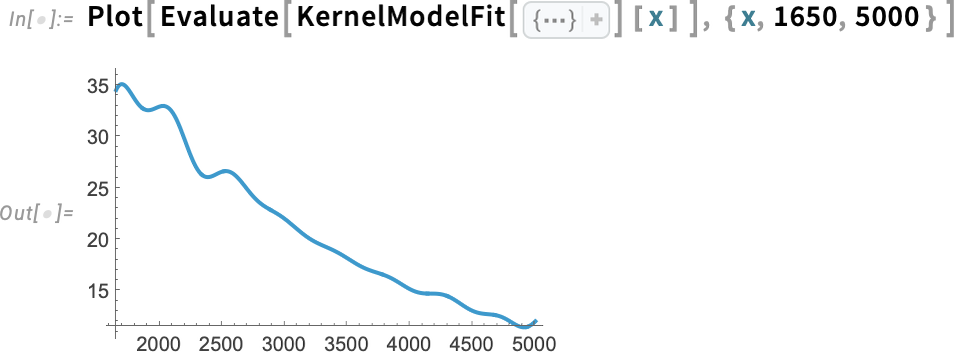
Alapértelmezés szerint a magfüggvények Gauss-féle eloszlásúak, és számukat, valamint szélességüket a rendszer automatikusan választja ki. Itt azonban például 20 darab Cauchy-magot kérünk, 10-es szélességgel:

 

Amit éppen ábrázoltunk, az egy legjobb illesztési görbe. A 14.3-as verzióban azonban, amikor egy FittedModel-t kapunk, nemcsak a legjobb illesztést kérhetjük le, hanem hibákkal együtt is, amelyeket az Around objektumok reprezentálnak:

 

Ezt ábrázolhatjuk úgy, hogy a legjobb illesztést, valamint a (95%-os konfidencia) sávgörbéket is megjelenítjük:

 

Ez azt mutatja, hogy a legjobb illesztés mellett az illesztés („statisztikai”) bizonytalansága is látható. Egy másik lehetőség, hogy ne az illesztéshez, hanem az összes eredeti adathoz jelenítsük meg a sávgörbéket:

 

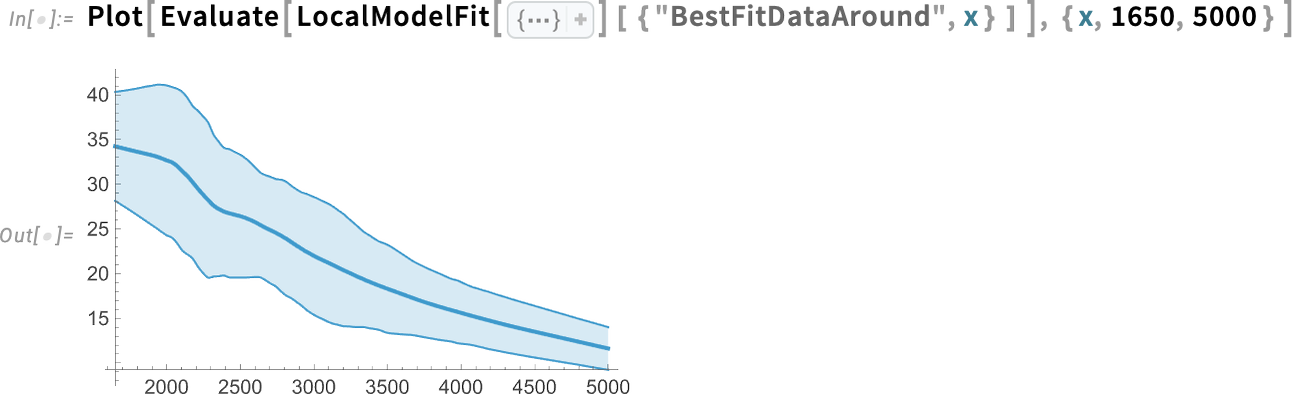
A ListFitPlot kifejezetten úgy van kialakítva, hogy illesztéseket ábrázoló grafikonokat készítsen. Ahogy az előbb láttuk, ilyen grafikonokat úgy is kaphatunk, ha először kifejezetten meghatározzuk az illesztéseket, majd azokat ábrázoljuk. Van azonban egy másik módja is, hogy illesztéseket tartalmazó grafikonokat kapjunk: az PlotFit opció hozzáadásával a „hagyományos” ábrázoló függvényekhez. Ez ugyanaz az PlotFit opció, amelyet a ListFitPlot-ban használhatunk az illesztés típusának megadására. Például egy olyan függvénynél, mint a ListPlot, ez azt jelenti, hogy illesztést adunk hozzá:

 

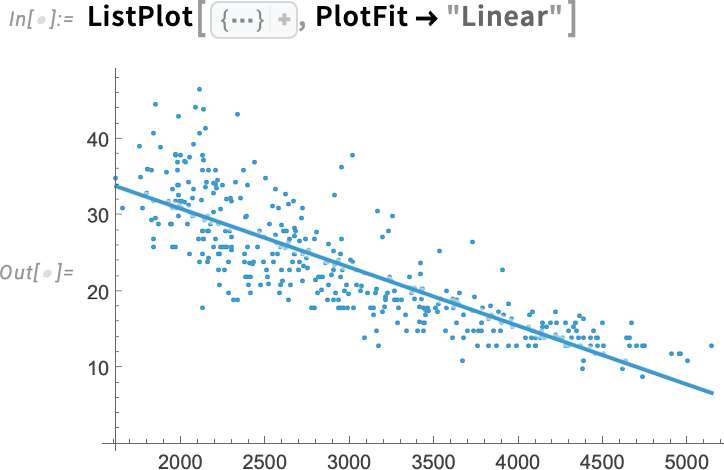
Egy olyan függvény, mint a ListLinePlot, úgy van kialakítva, hogy „vonalat húzzon az adatokon keresztül”, és a PlotFit segítségével (akárcsak az InterpolationOrder-rel) megadhatjuk, „milyen vonalat” húzzon. Itt például egy helyi modell alapján készült vonalat látunk:

 

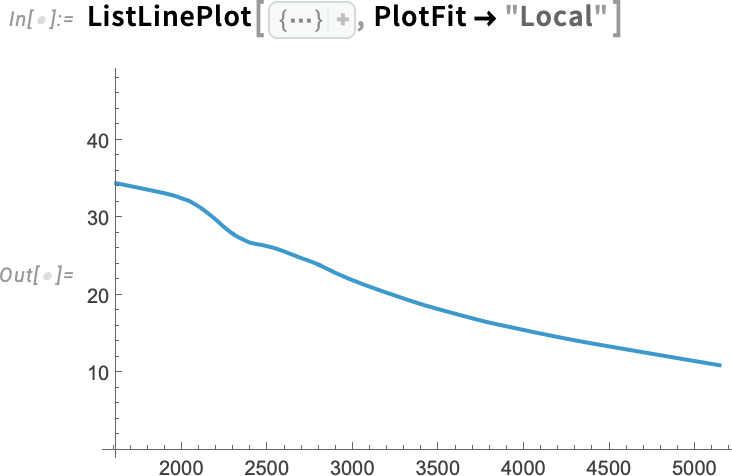
Lehetőség van arra is, hogy 3D-ben végezzünk illesztéseket. A 14.3-as verzióban, a ListFitPlot analógiájára, bevezetésre került a ListFitPlot3D, amely egy felületet illeszt egy 3D pontgyűjteményhez:

 

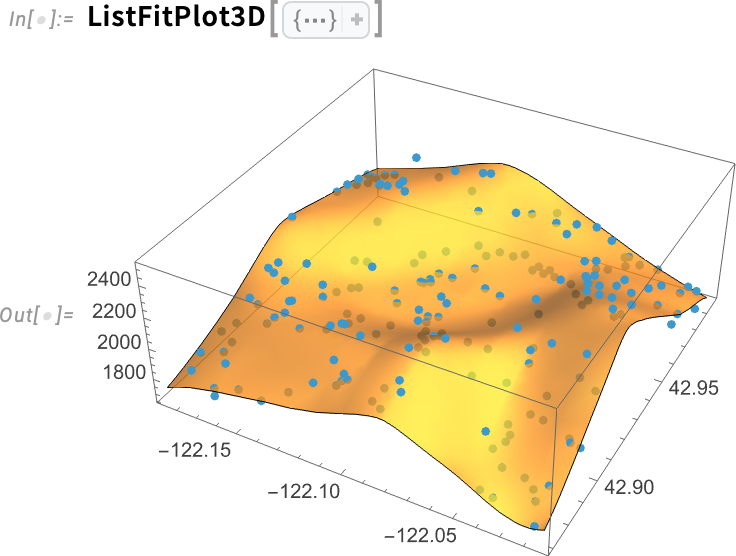
Íme, mi történik, ha a konfidenciasáv-felületeket is belefoglaljuk:

 

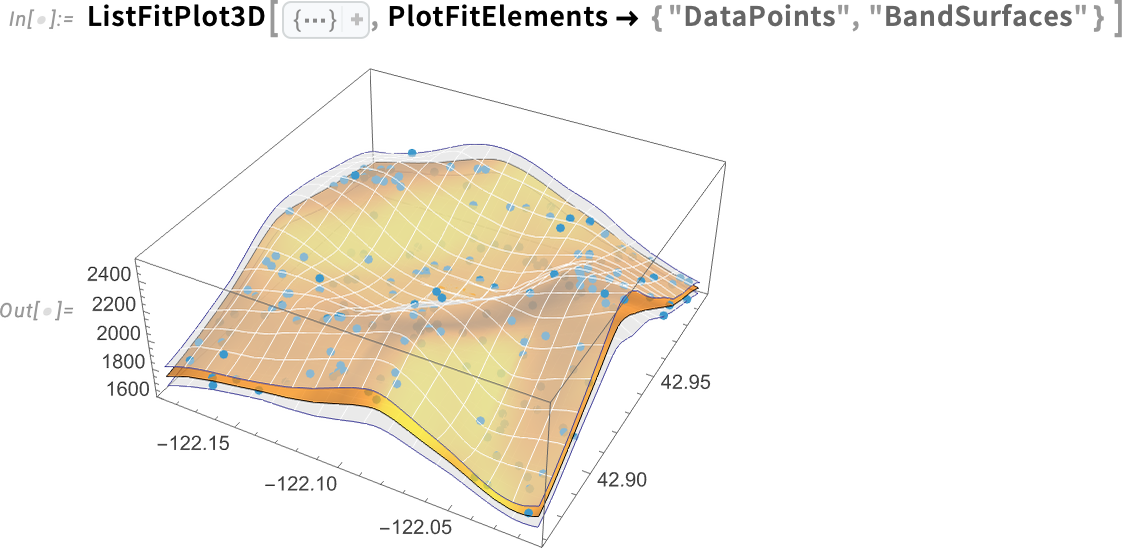
Az olyan függvények, mint a ListContourPlot, szintén lehetővé teszik az illesztéseket — sőt, néha jobb, ha egy kontúrdiagramon csak az illesztést ábrázoljuk. Például, íme egy „nyers” kontúrdiagram:

 

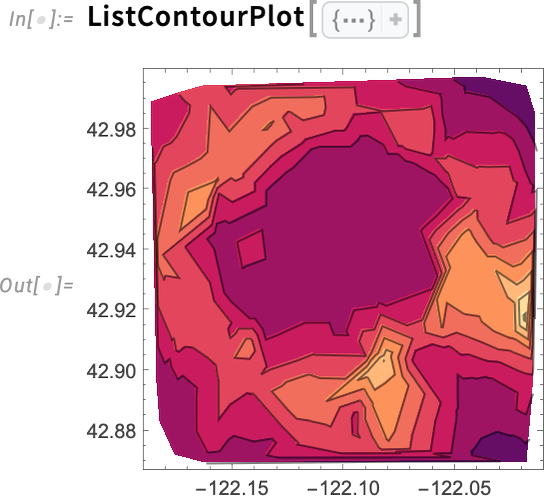
És íme, mit kapunk, ha nem a nyers adatokat, hanem a helyi modell illesztését ábrázoljuk az adatokra:

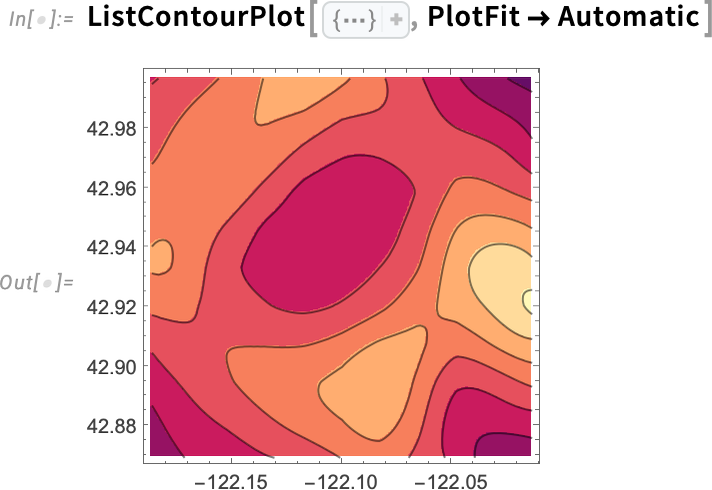
A térképek szebbek lesznek

 

A világ most jobban néz ki. Vagy pontosabban, a 14.3-as verzióban frissítettük a térképekhez használt stílusokat és megjelenítést:

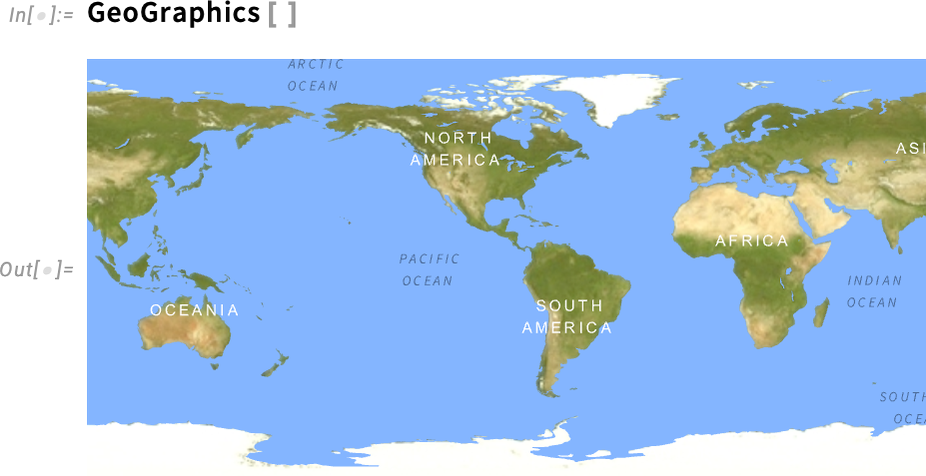
Mondanom sem kell, hogy ez ismét egy olyan terület, ahol a sötét móddal is foglalkoznunk kellett. Íme a megfelelő kép sötét módban:

 

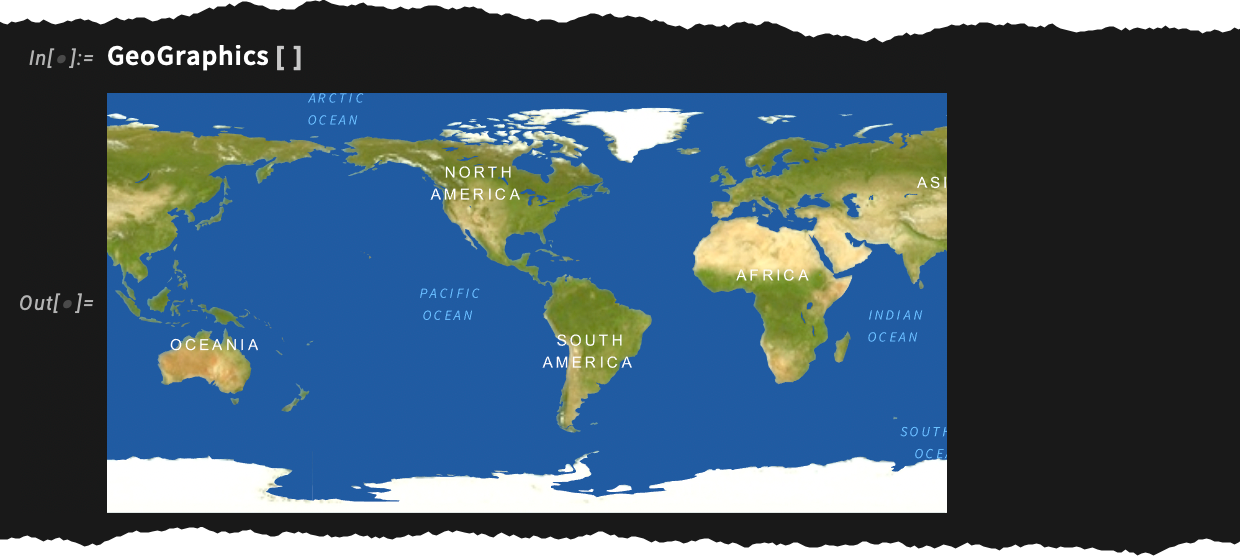
Ha egy kisebb területre fókuszálunk, a „domborzat” kezd halványabbá válni:

 

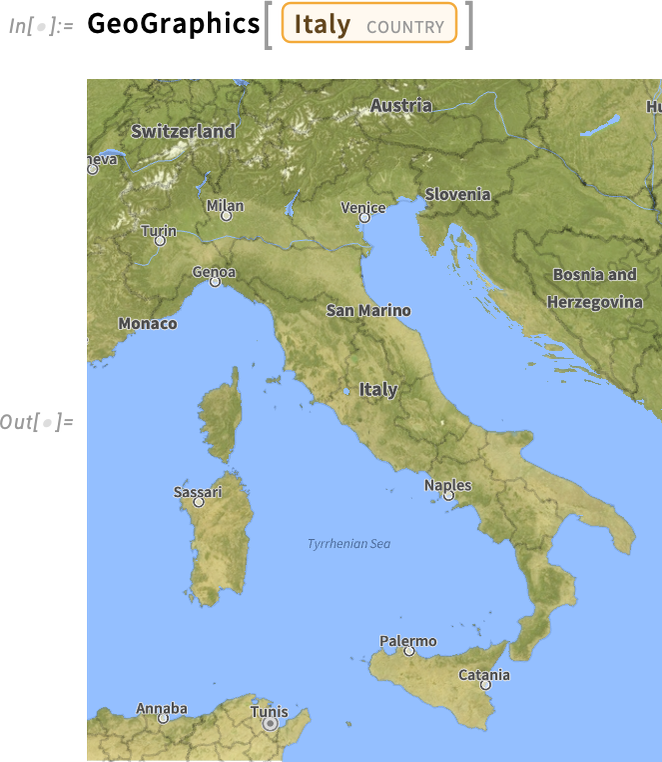
Városi szinten az utak válnak hangsúlyossá (és a 14.3-as verzióban új, élesebb színekkel jelennek meg):

 

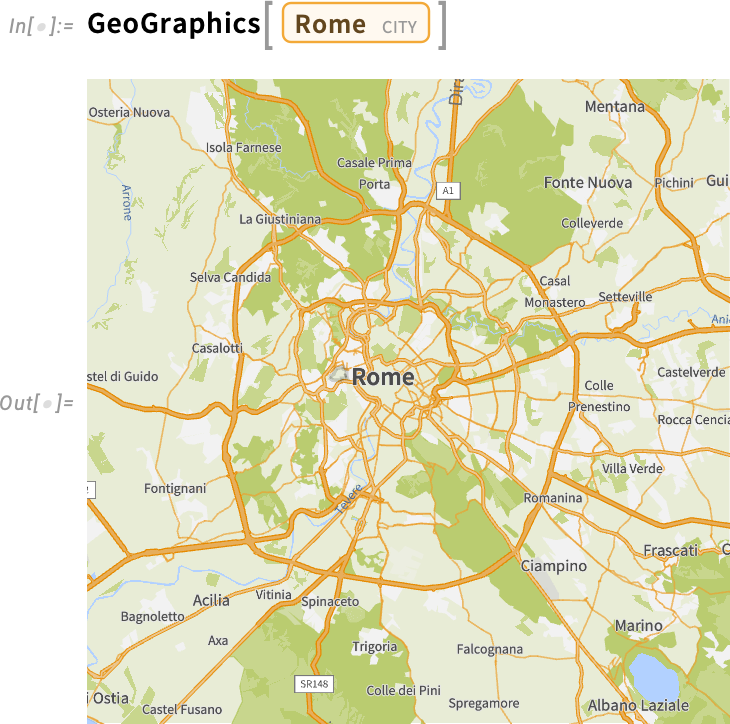
Ha tovább nagyítunk, több részlet válik láthatóvá:

 

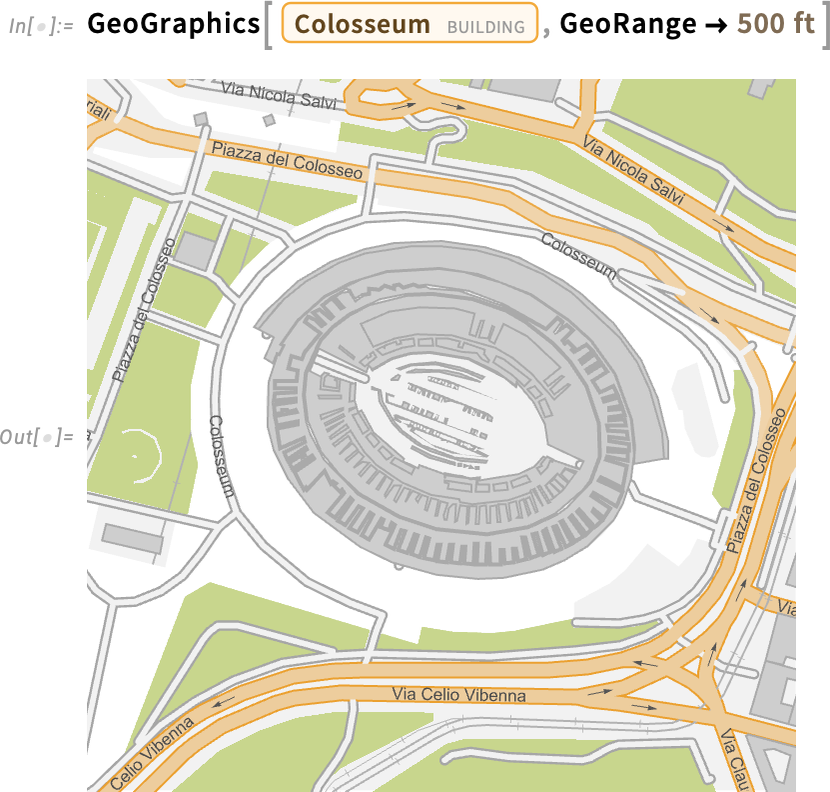
És igen, műholdképet is kaphatunk:

 

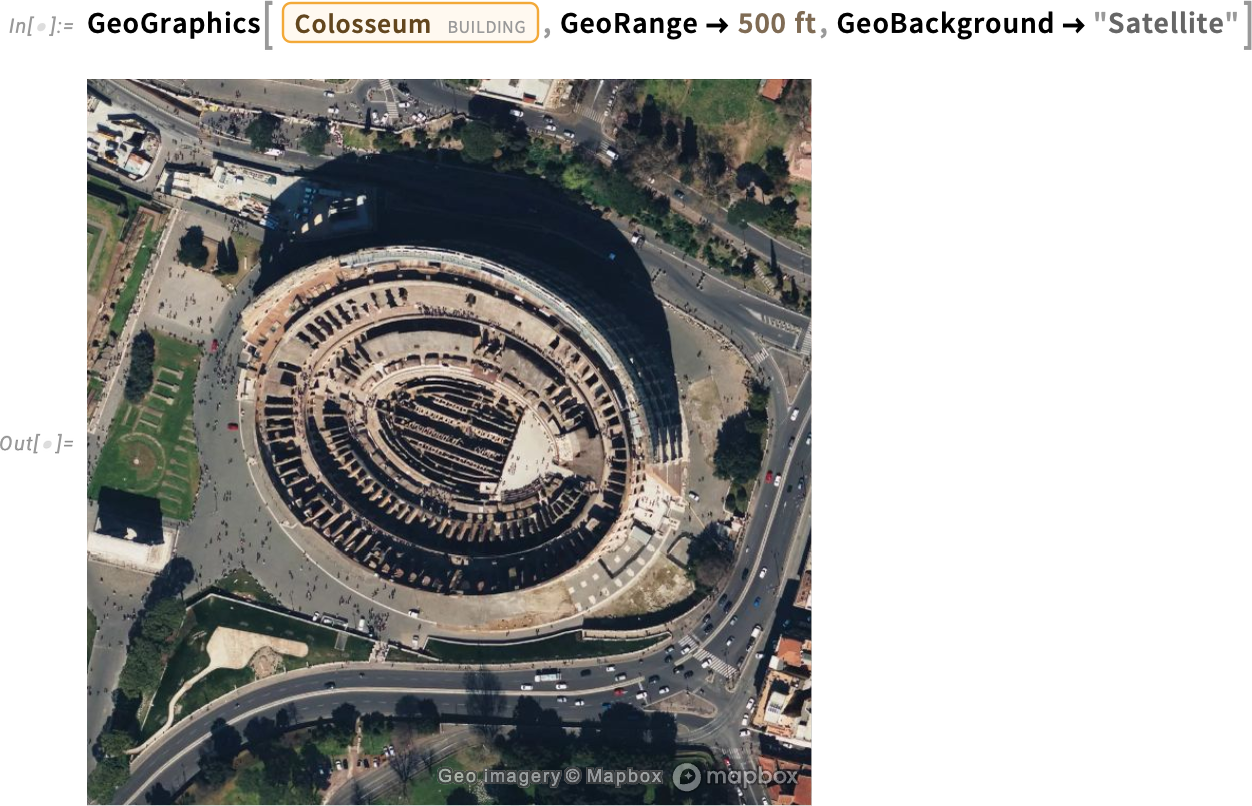
Minden rendelkezik sötét móddal:

 

Ezeknek a térképeknek egyik fontos jellemzője, hogy mind felbontástól független vektorgrafikával készülnek. Ezt a lehetőséget először a 12.2-es verzióban vezettük be opcióként, de a 14.3-as verzióban elég hatékonnyá tettük, hogy mostantól alapértelmezetté vált.

Egyébként a 14.3-as verzióban nemcsak sötét módban tudunk térképeket megjeleníteni, hanem tényleges éjszakai műholdképeket is kaphatunk:

 

Nagyon igyekeztünk, hogy szép, éles színeket válasszunk az alapértelmezett térképeinkhez. Néha azonban valójában azt szeretnénk, hogy az „alaptérkép” meglehetősen semleges legyen, mert a térképre ábrázolt adatoknak kell igazán kiemelkedniük. És ez történik alapértelmezés szerint az olyan függvényeknél, mint a GeoListPlot:

 

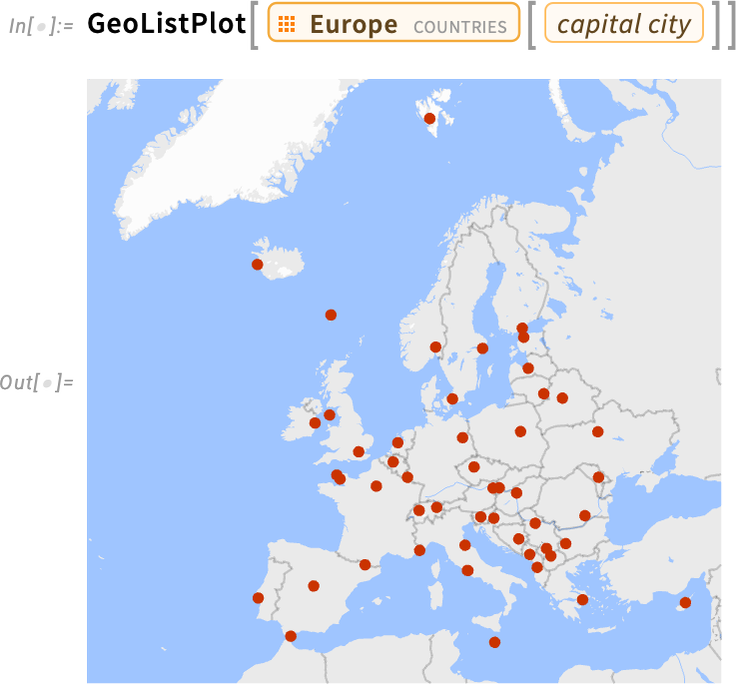
A térképkészítésnek végtelen számú finomsága van, amelyek közül néhány matematikailag meglehetősen összetett. Amit a 14.3-as verzióban végre sikerült megoldanunk, az az, hogy valódi gömbi geometriát alkalmazunk a vektorgrafikus térképadatokon. Ennek következményeként most már pontosan meg tudjuk jeleníteni (és levágni) még nagyon elnyújtott földrajzi jellegzetességeket is — például Ázsiát ebben a vetítésben:

 

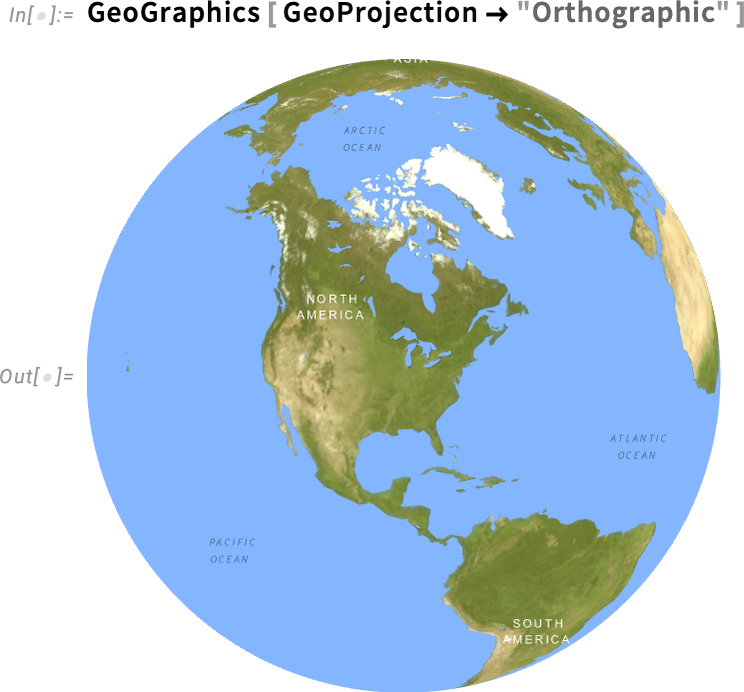
A 14.3-as verzió másik új földrajzi függvénye a GeoReposition, amely egy földrajzi objektum koordinátáit átalakítva máshová helyezi a Földön, miközben megtartja annak méretét. Például ez egészen jól szemlélteti, hogy egy adott eltolás és forgatás mellett Afrika és Dél-Amerika geometriailag illeszkedik egymáshoz (ami a kontinensvándorlásra utal):

 

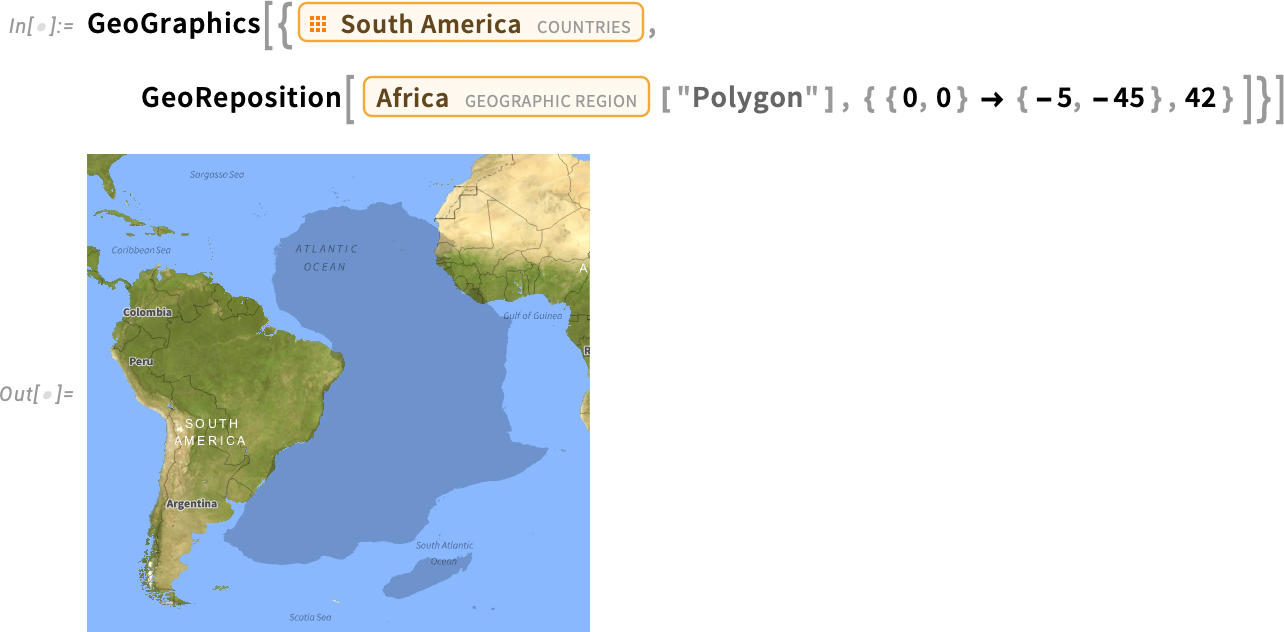
És igen, a Mercator-projekciós térképeken való megjelenése ellenére Grönland valójában nincs ilyen nagy:

 

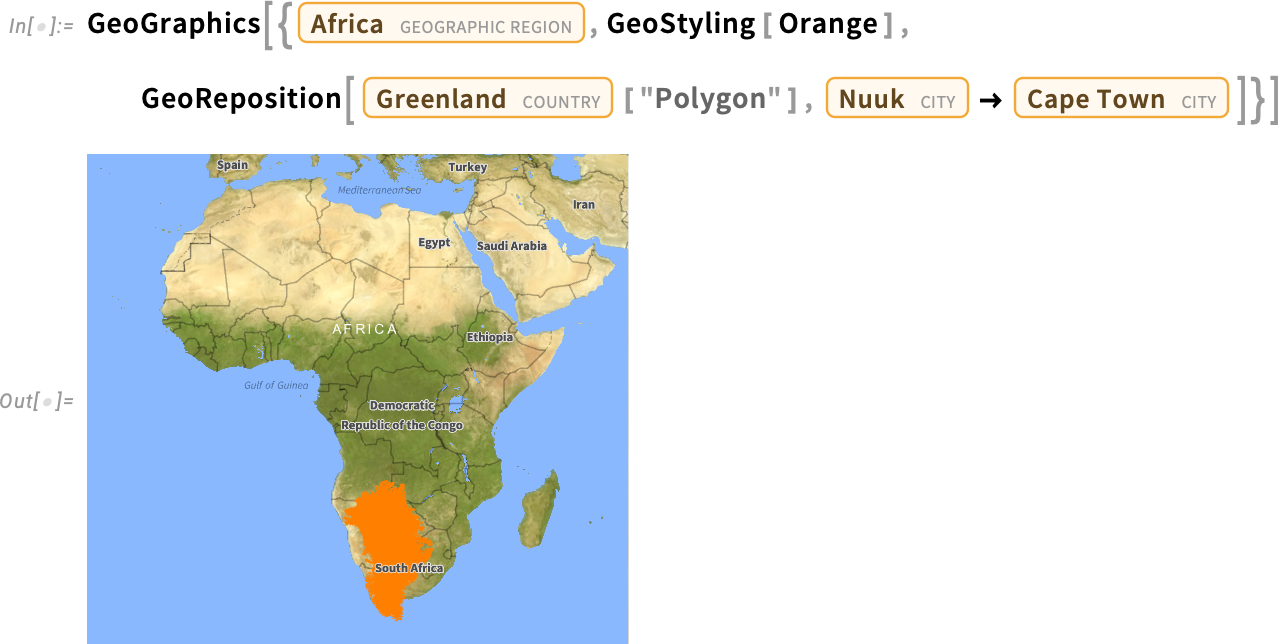
És mivel a Wolfram Language-ben mindig arra törekszünk, hogy a dolgokat a lehető legáltalánosabb módon valósítsuk meg, igen, ezt „a bolygón kívül” is megteheted:

 

 

 

 

 

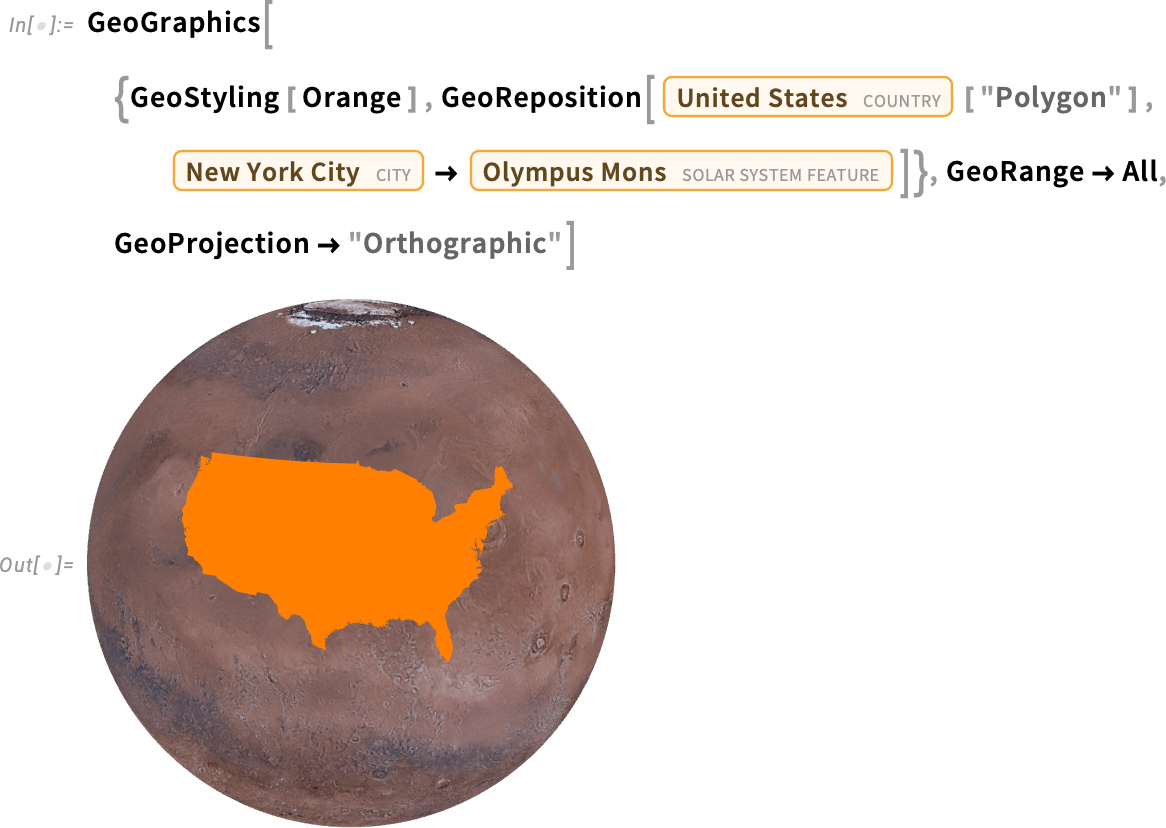
Egy jobb vörös: új elnevezett színek bemutatása

„Szeretném pirossal ábrázolni” — mondhatnánk. De mi is pontosan a piros? Csak a tiszta RGBColor[1,0,0], vagy valami kicsit eltérő? Több mint két évtizede vezettünk be olyan szimbólumokat, mint a Red, amelyek a „tiszta színeket”, például az RGBColor[1,0,0]-t jelölik. Azonban szép, „tervezett” képek készítésekor általában nem ezeket a „tiszta színeket” szeretnénk használni. Valójában számtalanszor előfordult velem, hogy egy kicsit „finomhangolni” akartam a pirosat, hogy jobban nézzen ki. Ezért a 14.3-as verzióban bevezetjük az új „standard színek” koncepcióját: például a StandardRed egy olyan piros változat, amely „pirosnak látszik”, de elegánsabb, mint a „tiszta piros”:

 

A különbség finom, de fontos. Más színek esetében ez kevésbé finom lehet:

Új standard színeink úgy lettek kiválasztva, hogy jól működjenek mind világos, mind sötét módban:

Nemcsak előtérszínként, hanem háttérszínként is jól működnek:

Ezek olyan színek is, amelyek ugyanazt a „színerősséget” képviselik, abban az értelemben, hogy — akárcsak az alapértelmezett ábrázoló színeink — hangsúly szempontjából kiegyensúlyozottak. Ráadásul úgy lettek kiválasztva, hogy jól harmonizáljanak egymással

Íme egy tömb az összes színről, amelyhez mostantól szimbólum tartozik (beleértve a White, Black és Transparent színeket is):

A „tiszta színek” és a „világos színek”, amelyek már régóta elérhetők, mellett most nemcsak a „standard színek” kerültek bevezetésre, hanem a „sötét színek” is.

Így most, amikor grafikákat készítesz, azonnal „tervezői minőségű” megjelenést adhatsz a színeknek egyszerűen azáltal, hogy a StandardRed, DarkRed stb. színeket használod a sima, régi Red helyett.

A sötét mód és a világos–sötét váltás története újabb kérdést vet fel a színek megadásában. Ha rákattintasz bármely színmintára egy jegyzetfüzetben, interaktív színválasztót kapsz:

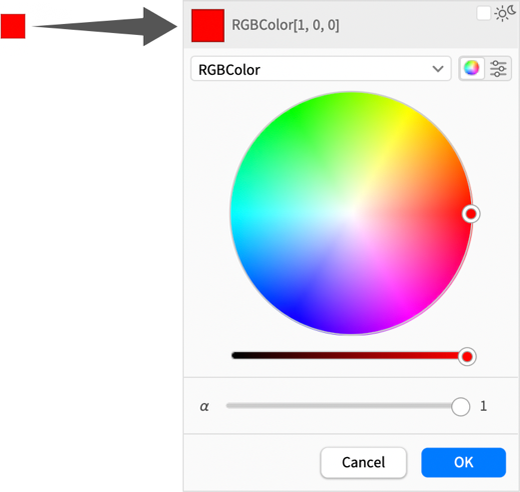
A 14.3-as verzióban azonban ez a színválasztó gyakorlatilag teljesen újratervezésre került, hogy kezelni tudja a világos és sötét módot, valamint általánosan egyszerűsítse a színek kiválasztását.

Korábban alapértelmezés szerint csúszkákkal kellett kiválasztani a színeket:

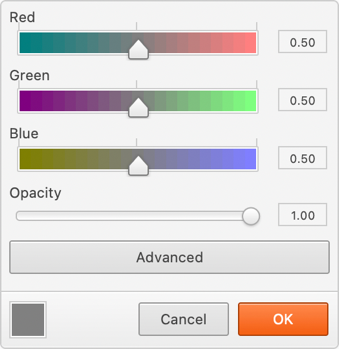
Most már van egy sokkal könnyebben használható színkör, kiegészítve fényerő- és átlátszósági csúszkákkal:

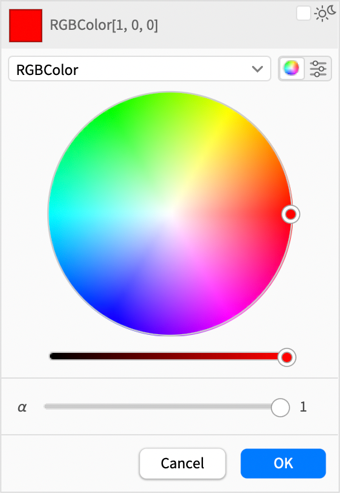
Ha továbbra is csúszkákat szeretnél, azokat is kérheted:

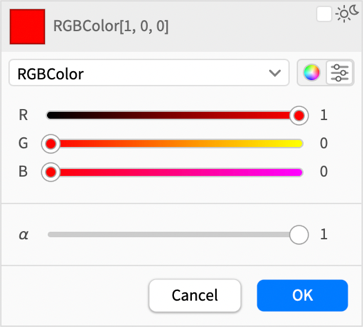
De most már különböző színtér-formátumokat is választhatsz — például a Hue-t, amely hasznosabbá teszi a csúszkákat:

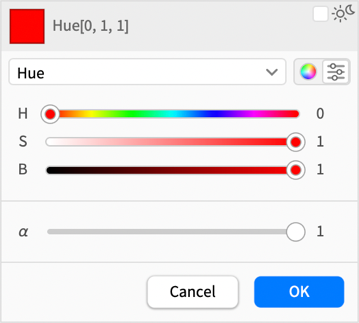
Mi a helyzet a világos–sötét váltással? Nos, a színválasztó most ezt a jobb felső sarkában tartalmazza

Ha rákattintasz, a kiválasztott szín automatikusan úgy lesz beállítva, hogy váltson a világos és sötét mód között:

Ha bármelyiket kiválasztod / , a következőt kapod:

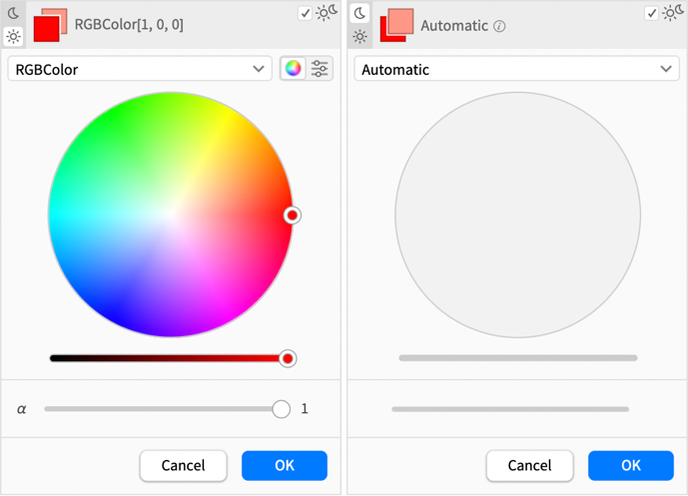
Más szóval, ebben az esetben a világos mód színét kifejezetten kiválasztottuk, míg a sötét mód színe automatikusan generálódott.

Ha tényleg minden fölött kontrollt szeretnél, a színtér menüt használhatod a sötét módhoz, és az Automatic helyett egy konkrét színtér-formátumot választhatsz, majd manuálisan kiválaszthatod a sötét mód színét abban a színtérben.

Érdekességként megemlíthető, hogy ha a jegyzetfüzeted sötét módban lenne, a dolgok fordítva működnének: alapértelmezés szerint a sötét mód színének kiválasztására kapnál lehetőséget, és a világos mód színe generálódna automatikusan.

 

 

 

 

További grafikai felfrissítés

A 14.2-es verzió számos nagyszerű új funkciót hozott. De egy „apró” fejlesztés, amit én személy szerint nap mint nap észreveszek és értékelek, az az alapértelmezett ábraszínek „feldobása”. Már az is, hogy a helyett , a helyett , a helyett került, azonnal több „életet” vitt a grafikákba, és összességében sokkal „csinosabbá” tette őket. Most pedig a 14.3-as verzióban tovább vittük ezt a folyamatot, és még több függvény által generált alapértelmezett színt „feldobtunk”.

Például a 14.2-es verzió előtt a DensityPlot alapértelmezett színei a következők voltak:

 

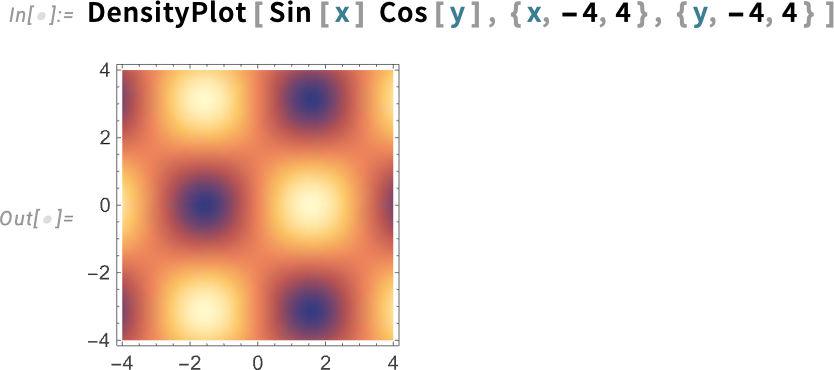
de most „nagyobb lendülettel” ezek:

 

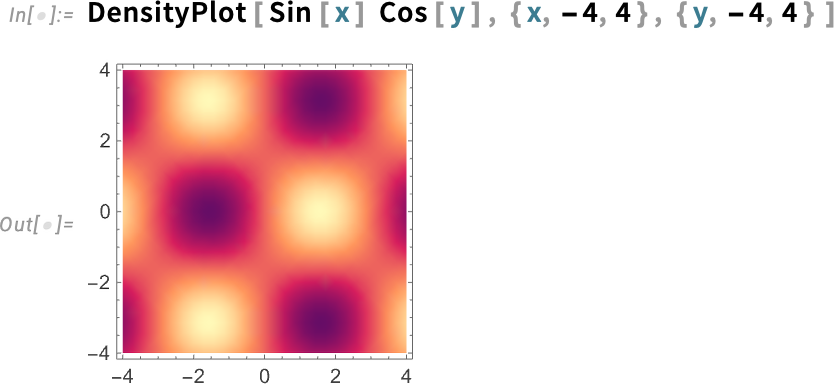
Egy másik példa — ami számomra különösen érdekes, mint a celluláris automaták régóta foglalkozó kutatója számára — az ArrayPlot frissítése. Alapértelmezés szerint az ArrayPlot szürkeárnyalatokat használ az egymást követő értékekhez (itt csak 0, 1, 2):

 

De a 14.3-as verzióban megjelent egy új beállítás — ColorRules → “Colors” — amely ehelyett színeket használ:

 

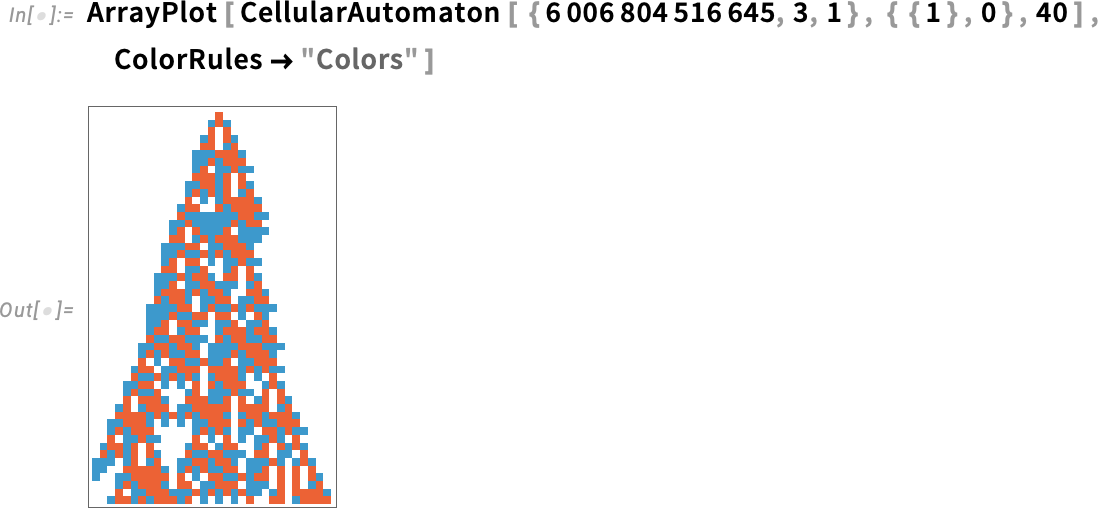
És igen, nagyobb értékszámok esetén is működik:

 

Valamint sötét módban:

 

Egyébként a 14.3-as verzióban a rácsok (meshes) kezelését is továbbfejlesztettük — így amikor sok cella van, azok fokozatosan elhalványulnak:

 

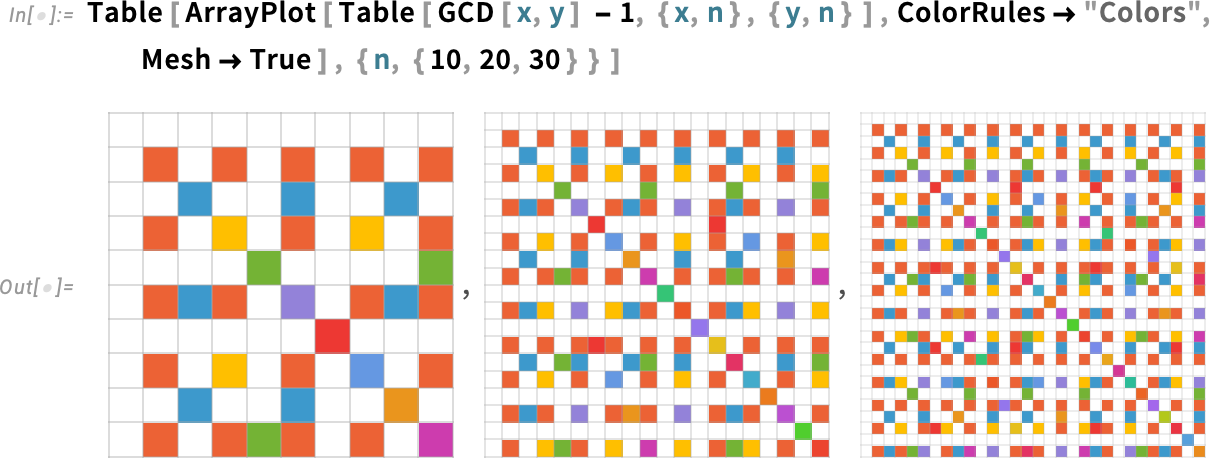
És mi a helyzet a 3D-vel? Még ott is megváltoztattuk az alapértelmezést: már pusztán a 0 és 1 értékek esetén is megjelenik egy kis szín:

 

A rendszer számos területén történtek frissítések a színekben (és a megjelenítés egyéb részleteiben is). Egy példa erre a bizonyítási objektumok megjelenése. A 14.2-es verzióban egy tipikus bizonyítási objektum így nézett ki:

 

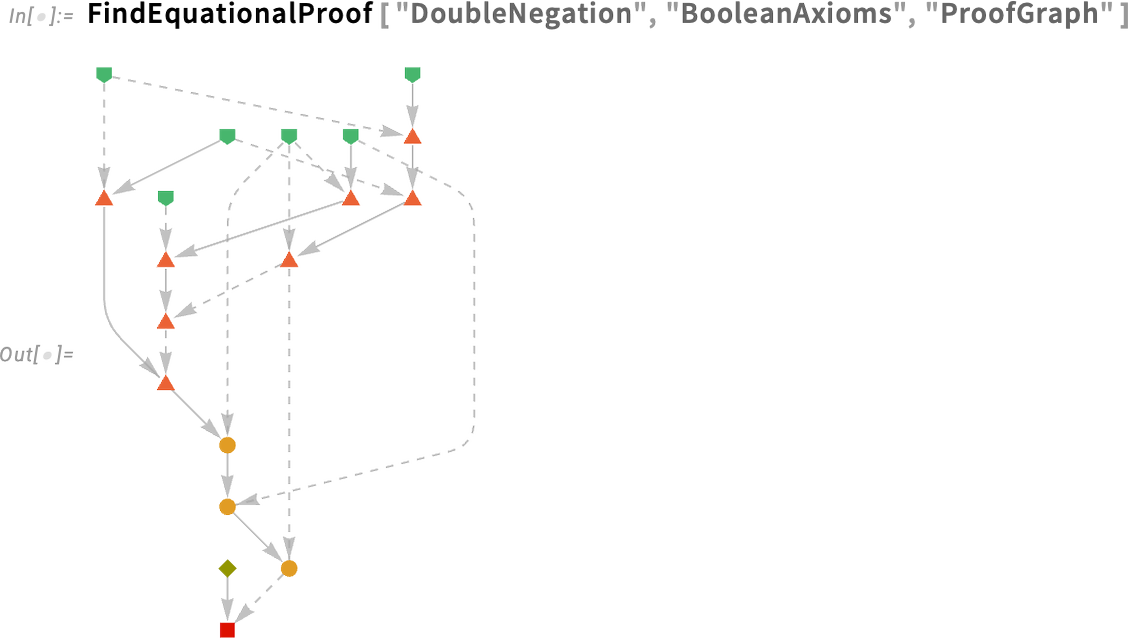
Most a 14.3-as verzióban (szerintünk) egy kicsit elegánsabban néz ki:

 

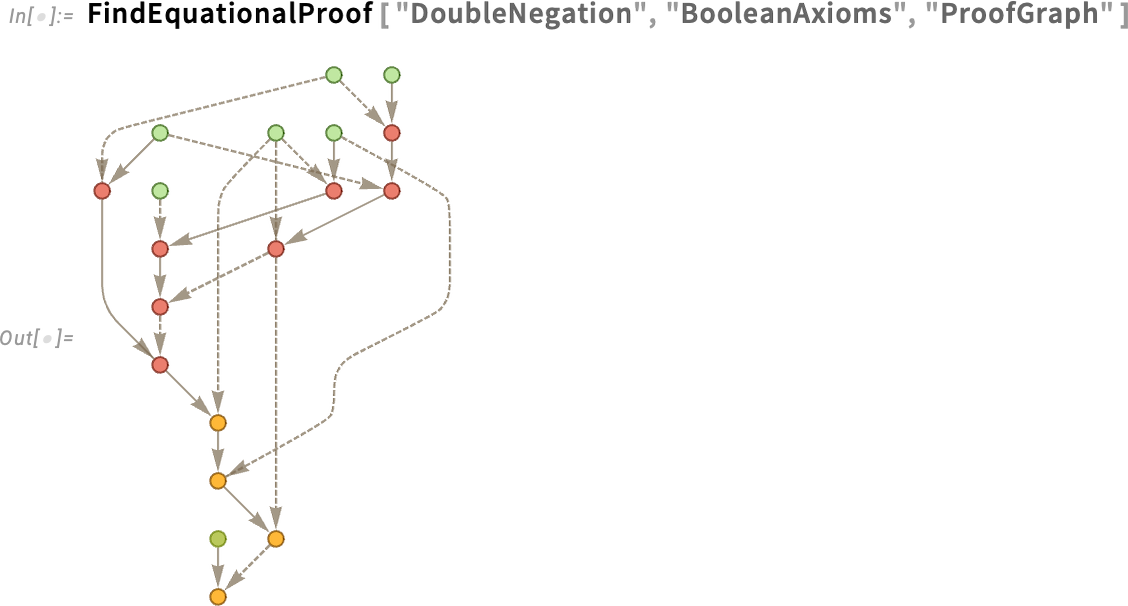
A színeken túl a 14.3-as verzió egy másik jelentős újdonsága a diagramokon megjelenő feliratok kezelése. Íme egy jellemzőtér-ábra az országzászlók képeiről:

 

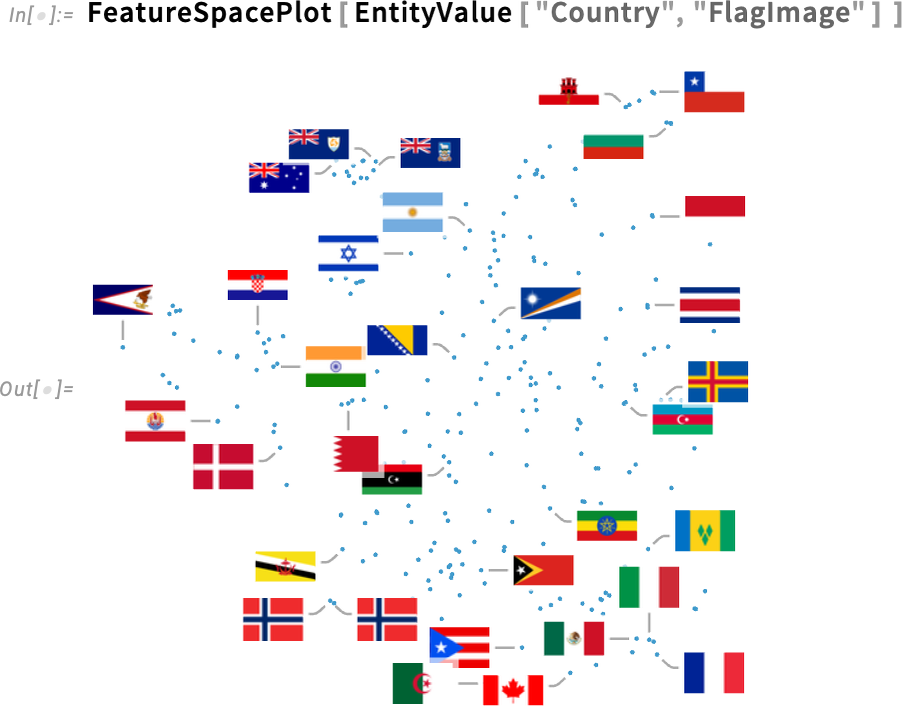
Alapértelmezés szerint néhány pont kap címkét, míg mások nem. Az alkalmazott heurisztika igyekszik a címkéket üres területekre elhelyezni, és amikor nincs elég hely (vagy a címkék túlzottan átfednék egymást), akkor egyszerűen elmaradnak. A 14.2-es verzióban az egyetlen választási lehetőség az volt, hogy legyenek-e címkék, vagy sem. A 14.3-as verzióban azonban megjelent egy új beállítás, a LabelingTarget, amely meghatározza, mire törekedjen a rendszer a címkék elhelyezésekor.

Például a LabelingTarget → All beállítással minden pont kap címkét, még akkor is, ha ez azt jelenti, hogy a címkék átfedik egymást vagy magukat a pontokat:

 

A LabelingTarget több kényelmes beállítást is kínál. Az egyik példa erre a “Dense” beállítás:

 

Adhatunk meg számot is, amellyel azt határozzuk meg, hogy a pontok hányadát címkézzük:

 

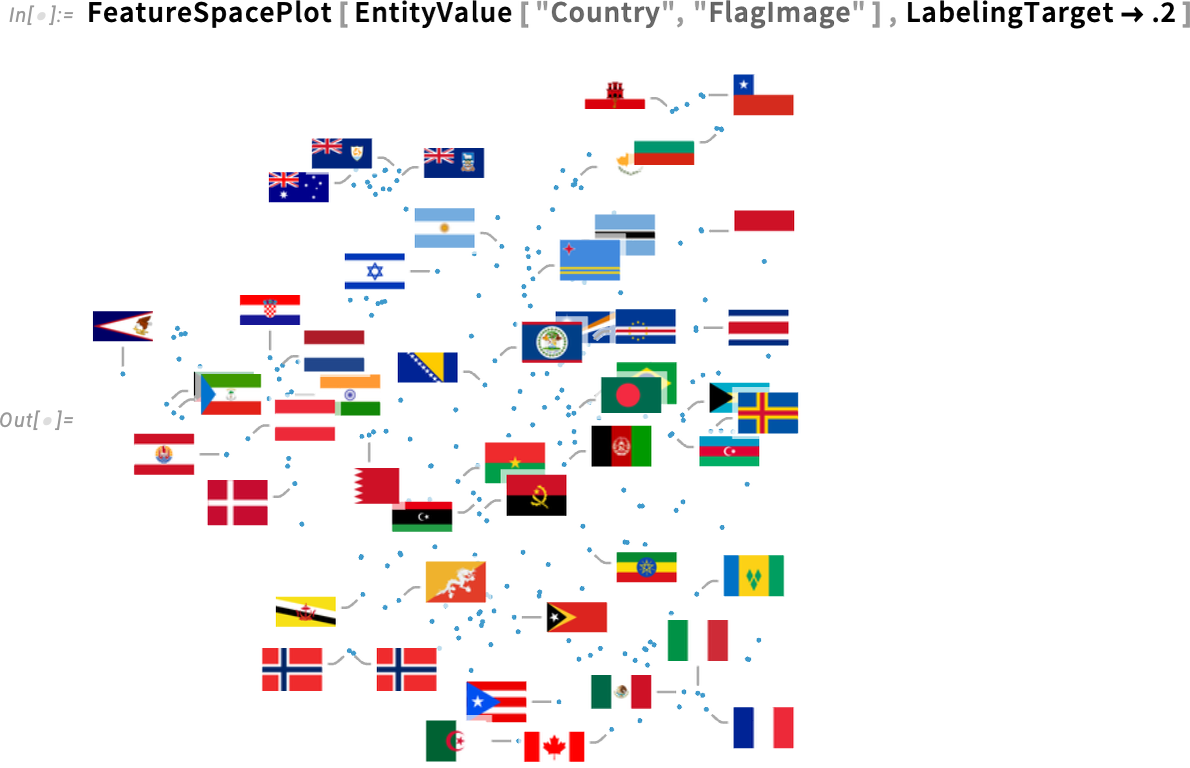
Ha részletesebben szeretnénk beállítani, megadhatunk egy asszociációt is. Például itt azt határozza meg, hogy minden címke vezetővonala kizárólag vízszintes vagy függőleges legyen, ne legyen átlós:

 

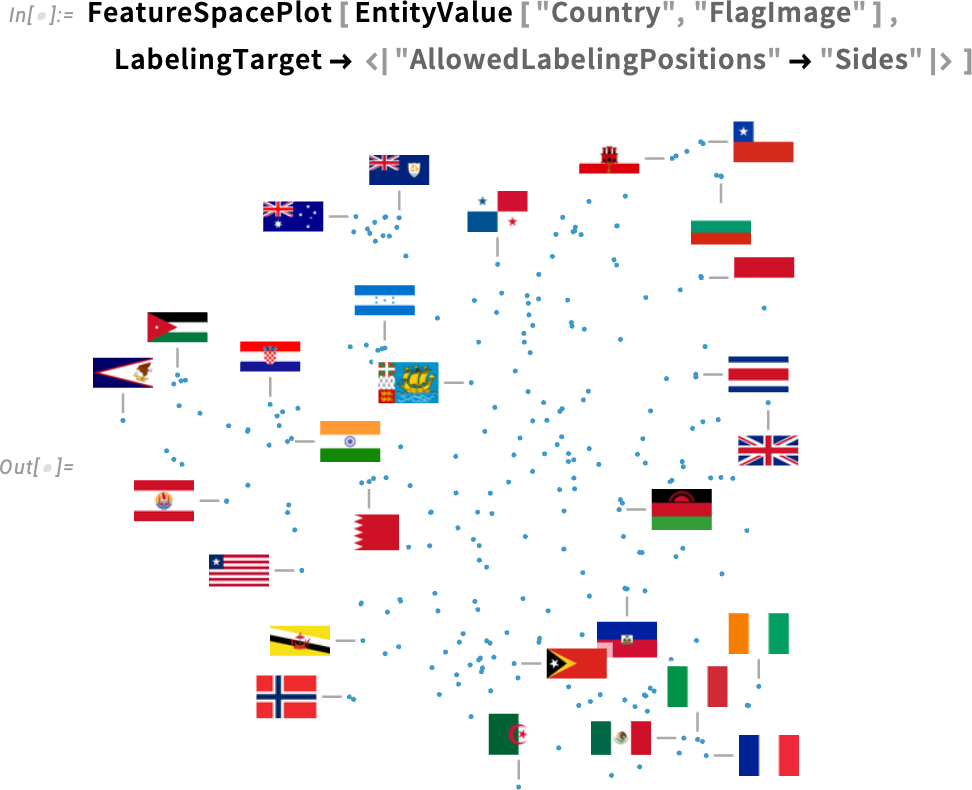
A LabelingTarget opciót a pontokat kezelő vizualizációs függvények teljes skálájában támogatják, mind 2D-ben, mind 3D-ben. Alapértelmezés szerint ebben az esetben a következő történik:

 

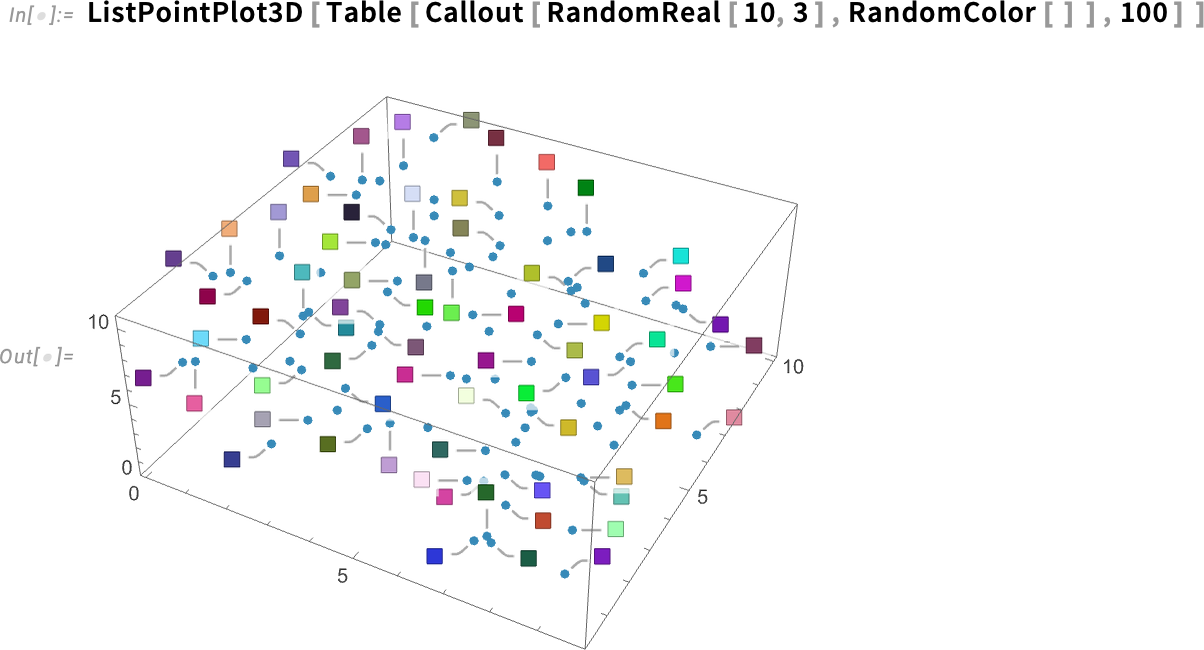
És íme, mi történik, ha a “20% coverage” beállítást kérjük:

 

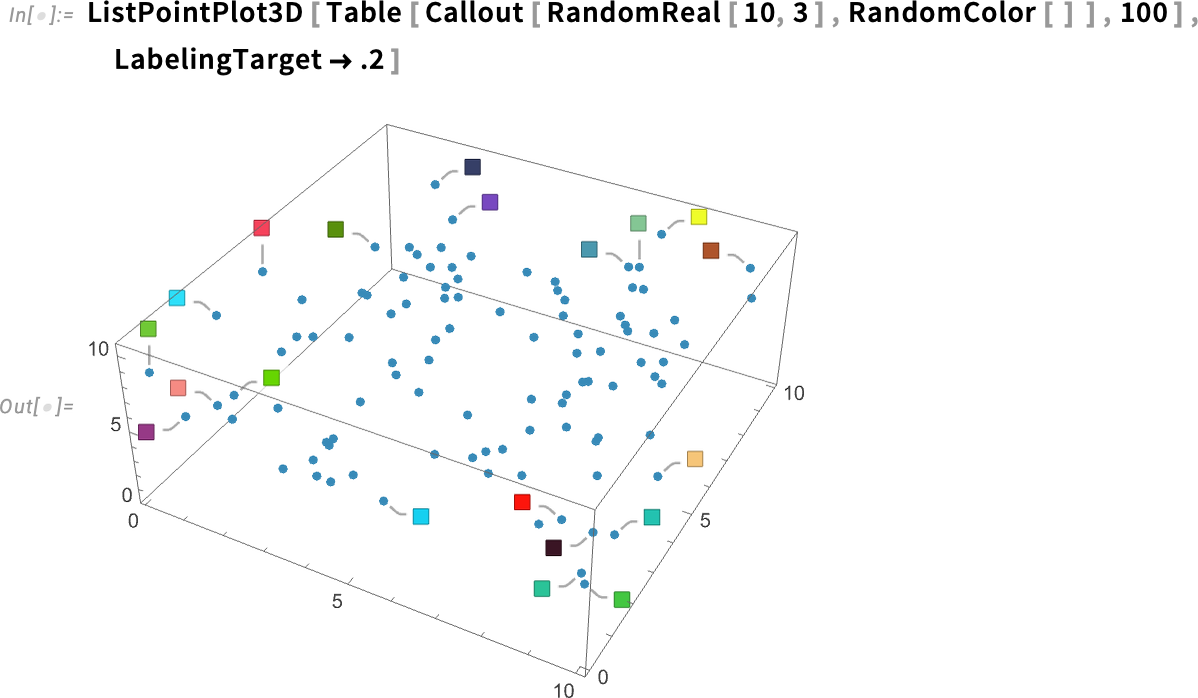
A 14.3-as verzióban számos új fejlesztés történt a vizualizációs képességeink terén, de van egy (nagyon hasznos) funkció is, amit akár „leminősítésnek” is tekinthetünk: a PlotInteractivity opció, amellyel egy adott ábrán kikapcsolhatjuk az interaktivitást. Például a PlotInteractivity → False beállítással a hisztogram osztályai soha nem „ugranak fel”, amikor föléjük viszed az egeret. Ez különösen hasznos, ha nagy és összetett grafikák hatékonyságát szeretnénk biztosítani, vagy ha az ábrákat nyomtatásra szánjuk, ahol az interaktivitás soha nem lesz releváns.

 

 

 

Nem kommutatív algebra

A „számítógépes algebra” már a 1.0-ás verzió egyik kulcsfunkciója volt 1988-ban. Ez főként polinomokkal, racionális függvényekkel stb. végzett műveleteket jelentett — bár természetesen az általános szimbolikus nyelvünk mindig lehetővé tette sok általánosítás elvégzését. Már az 1.0-ás verzióban is létezett a NonCommutativeMultiply szimbólum (beírva: **), amelyet a „nem-kommutatív szorzás általános formájának” reprezentálására szántak. Amikor bevezettük, gyakorlatilag csak egy helykitöltő volt, és leginkább „a jövőbeli bővítésre fenntartották”.

Nos, 37 évvel később, a 14.3-as verzióban az algoritmusok készen állnak, és a jövő elérkezett! Most végre számításokat végezhetünk a NonCommutativeMultiply-val. Az eredmények nemcsak a „nem-kommutatív szorzás általános formájára” használhatók, hanem például szimbolikus tömbök egyszerűsítésére is.

Az 1.0-ás verzió óta a NonCommutativeMultiply-t be lehetett írni **-ként. A 14.3-as verzió első nyilvánvaló újdonsága, hogy most a ** automatikusan ⦻-ra alakul. A ⦻-val végzett matematikai műveletek támogatására most már létezik a GeneralizedPower, amely az ismételt nem-kommutatív szorzást képviseli, és kis ponttal jelzett kitevőként jelenik meg:

És mi a helyzet a ⦻-t tartalmazó kifejezéseken végzett műveletekkel? A 14.3-as verzióban rendelkezésre áll a NonCommutativeExpand:

 

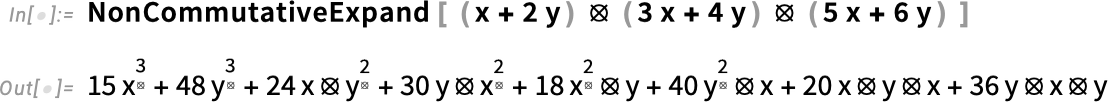
Ezzel a kibővítéssel egy kanonikus formát kapunk a nem-kommutatív polinomunkhoz. Ebben az esetben a FullSimplify képes azt egyszerűsíteni:

 

bár általánosságban nincs egyértelmű „faktorizált” alakja a nem-kommutatív polinomoknak, és bizonyos (viszonylag ritka) esetekben az eredmény eltérhet attól, amiből kiindultunk.

A ⦻ egy teljesen általános, további relációk nélküli nem-kommutatív szorzási formát jelöl. Ugyanakkor a nem-kommutatív szorzásnak számos más, hasznos formája is létezik. Egy fontos példa erre a . (Dot). A 14.2-es verzióban bevezettük az ArrayExpand függvényt, amely szimbolikus tömbökön működik:

 

Most pedig rendelkezésre áll a NonCommutativeExpand, amely beállítható úgy, hogy a Dot műveletet használja szorzásként:

 

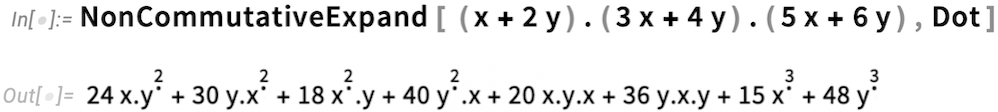
Az eredmény másképp néz ki, mert a GeneralizedPower-t használja. De a FullSimplify segítségével ellenőrizhetjük az ekvivalenciát:

 

A nem-kommutatív szorzás köré bevezetett új algoritmusok most már lehetővé teszik erőteljesebb szimbolikus tömbműveletek elvégzését is, például az alábbi tömbegyszerűsítést:

 

Hogyan működik mindez? Nos, legalábbis többváltozós esetekben a nem-kommutatív Gröbner-bázisok egy változatát használja. A Gröbner-bázisok a hagyományos, kommutatív polinomszámítás egyik alapvető módszerét jelentik; a 14.3-as verzióban pedig ezt általánosítottuk a nem-kommutatív esetre is:

 

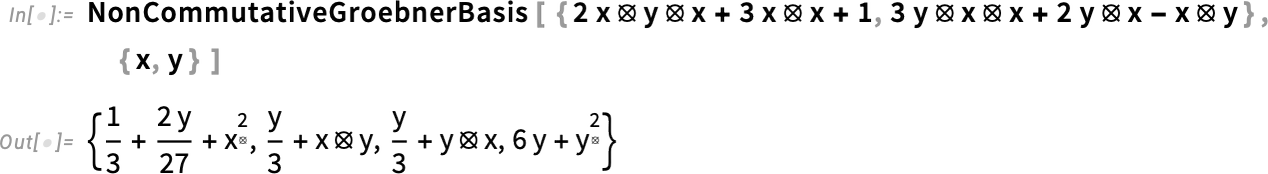
Hogy képet kapjunk arról, milyen jellegű dologról van szó, nézzünk meg egy egyszerűbb esetet:

 

A bemenetet úgy is felfoghatjuk, mint olyan kifejezések listáját, amelyekről feltételezzük, hogy nullák. Ha például szerepel benne az a ⦻ b − 1, akkor ezzel lényegében azt állítjuk, hogy a ⦻ b = 1, vagy másképp fogalmazva: b az a jobb oldali inverze. Így tehát azt mondjuk, hogy b az a jobb inverze, míg c a bal inverze. Az így kapott Gröbner-bázis tartalmazza a b − c kifejezést is, ami azt mutatja, hogy az általunk megadott feltételek azt implikálják, hogy b − c = 0, vagyis b egyenlő c-vel.

A nem-kommutatív algebrák sok területen megjelennek, nemcsak a matematikában, hanem a fizikában is (különösen a kvantumfizikában). Emellett használhatók a funkcionális programozás egyfajta szimbolikus reprezentációjaként is. Itt például az f szerint gyűjtjük össze a tagokat, ahol a szorzás művelete a függvénykompozíciót jelenti.

 

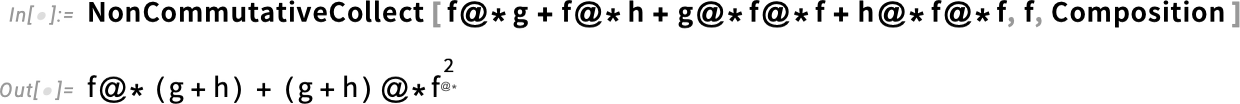
A nem-kommutatív algebra számos alkalmazásában hasznos a kommutátor fogalma:

 

És igen, ellenőrizhetjük híres kommutációs relációkat is, például a fizikából ismerteket:

 

(Létezik AntiCommutator is.)

Egy olyan függvény, mint a NonCommutativeExpand, alapértelmezés szerint azt feltételezi, hogy egy nem-kommutatív algebrával dolgozunk, ahol az összeadás + (Plus) jelöléssel történik, a szorzás ⦻ (NonCommutativeMultiply) segítségével, továbbá 0 az összeadás egysége, 1 pedig a szorzás egysége.

Ha azonban megadunk egy második argumentumot, a NonCommutativeExpand-nek jelezhetjük, hogy egy másik nem-kommutatív algebrát szeretnénk használni. Például {Dot, n} egy n×n-es mátrixokból álló algebrát jelöl, ahol a szorzás a . (Dot) művelettel történik, az egység pedig például (SymbolicIdentityArray[n]). A TensorProduct egy formális tenzorokból álló algebrát képvisel, ahol a szorzás művelete a ⊗ (TensorProduct). Általánosságban azonban saját nem-kommutatív algebrát is definiálhatunk a NonCommutativeAlgebra segítségével.

 

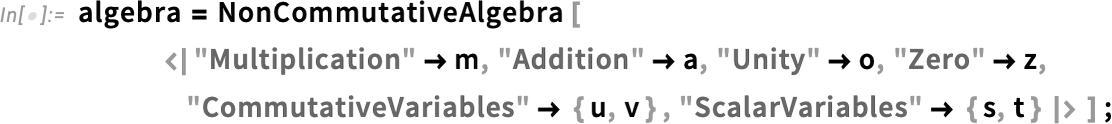
Most már ki tudjuk bővíteni egy kifejezést, feltételezve, hogy ez az algebra egy eleme (figyeljük a kis m-eket a generalizált “m hatványokban”):

 

 

 

 

 

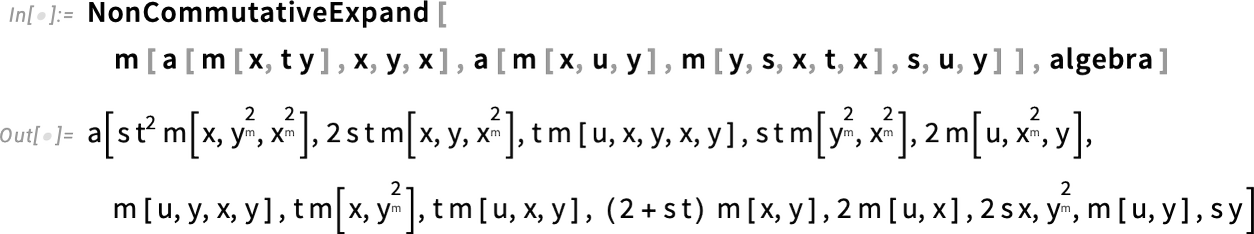
Rajzolás erre a felületre: Régiók vizuális annotációja

Van egy x, y, z változókat tartalmazó függvényünk, és van egy felület, amely 3D-ben van beágyazva. De hogyan ábrázolhatjuk ezt a függvényt a felületen? Nos, a 14.3-as verzióban erre is van egy függvény:

 

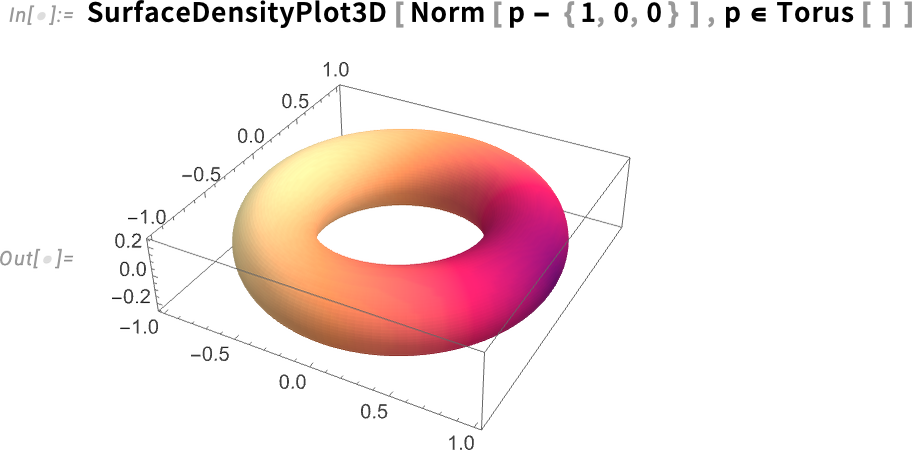
Ezt bármilyen típusú régió felületén elvégezhetjük:

 

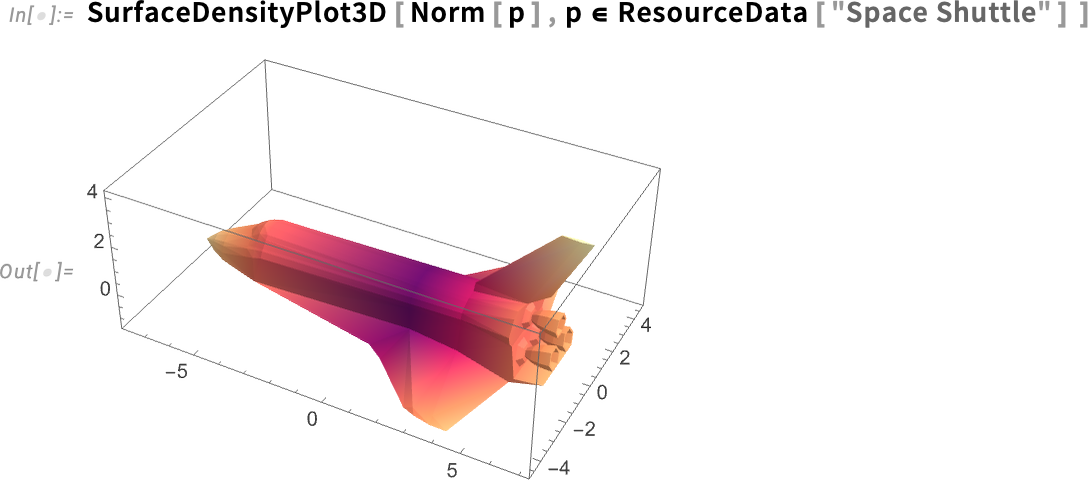
Létezik egy kontúrdiagram-változat is:

 

De mi van akkor, ha nem a teljes függvényt szeretnénk ábrázolni a felületen, hanem csak egy bizonyos részt kiemelni? Ebben az esetben használhatjuk az új HighlightRegion függvényt. A HighlightRegion-nek megadjuk az eredeti régiót, és azt a részt, amelyet ki szeretnénk emelni. Például az alábbi példában 200 pontot emelünk ki egy gömb felületén (és igen, a HighlightRegion helyesen gondoskodik arról, hogy a pontok láthatóak legyenek, és ne „vágja át” őket a felület):

 

Itt egy gömbsapkát emelünk ki (amelyet úgy adunk meg, hogy a gömb és a gömbfelszín metszetével definiáljuk):

 

A HighlightRegion nemcsak 3D-ben működik, hanem bármilyen dimenziójú régiók esetén is:

 

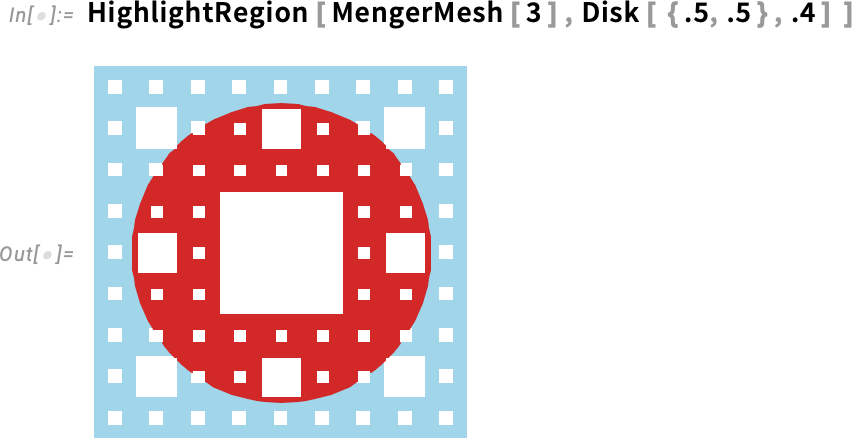
Visszatérve a felületeken értelmezett függvényekhez, a 14.3-as verzió egy másik kényelmes újdonsága, hogy a FunctionInterpolation most már tetszőleges régiókon is működik. A FunctionInterpolation célja, hogy egy függvényből (amelynek kiszámítása lassú lehet) egy InterpolatingFunction objektumot hozzon létre, amely közelíti a függvényt. Íme egy példa, ahol most egy viszonylag egyszerű függvényt interpolálunk egy bonyolult régión:

 

Most már a SurfaceDensityPlot3D segítségével ábrázolhatjuk az interpolált függvényt a felületen:

 

 

 

 

 

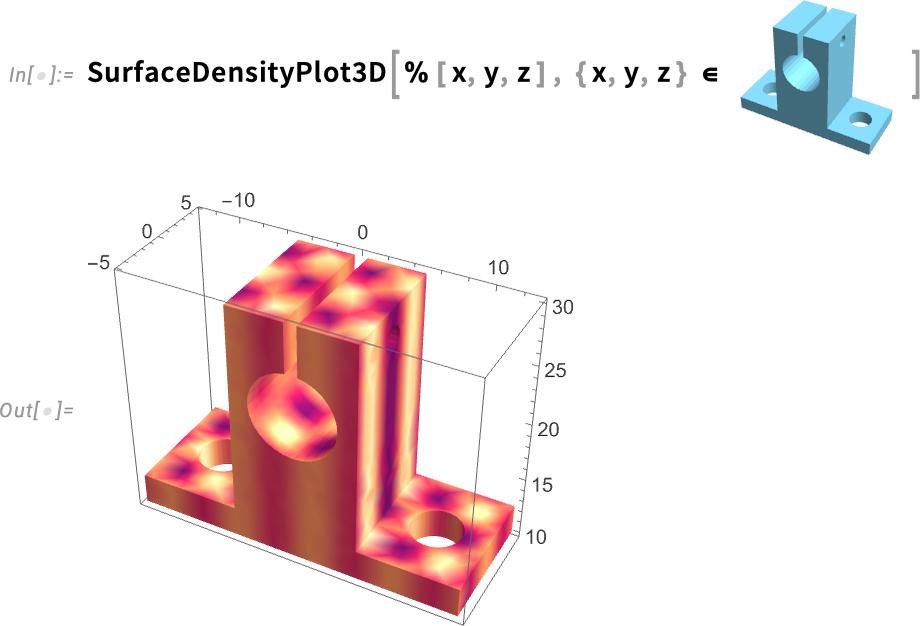
Görbületszámítás és -megjelenítés

Tegyük fel, hogy van egy 3D objektumunk:

 

A 14.3-as verzióban most már ki tudjuk számítani egy 3D objektum felületének Gauss-görbületét. Itt a SurfaceContourPlot3D függvényt használjuk, hogy egy értéket ábrázoljunk a felületen, ahol a p változó a felület pontjain változik:

 

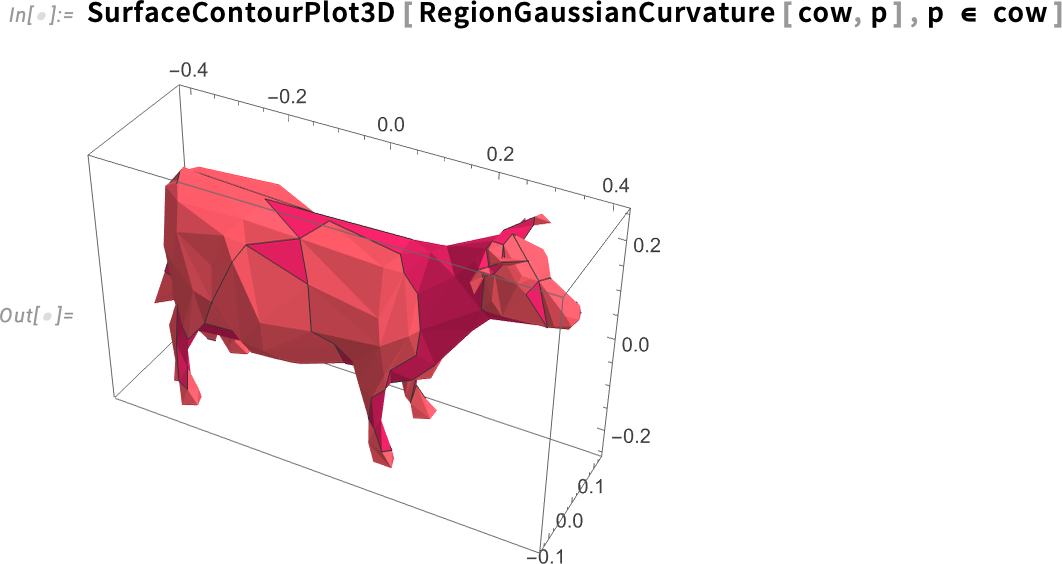
Ebben a példában a 3D objektumunkat teljesen egy háló (mesh) határozza meg. De tegyük fel, hogy van egy paraméterezett objektumunk:

 

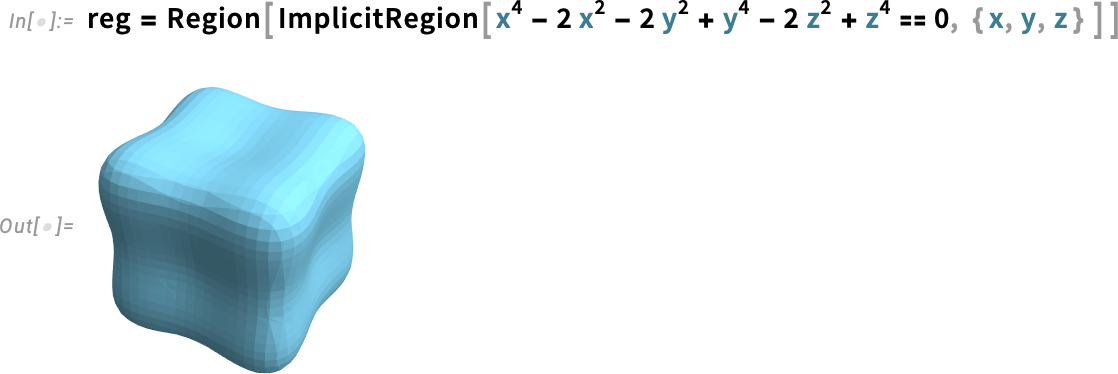
Ismét ki tudjuk számítani a Gauss-görbületet:

 

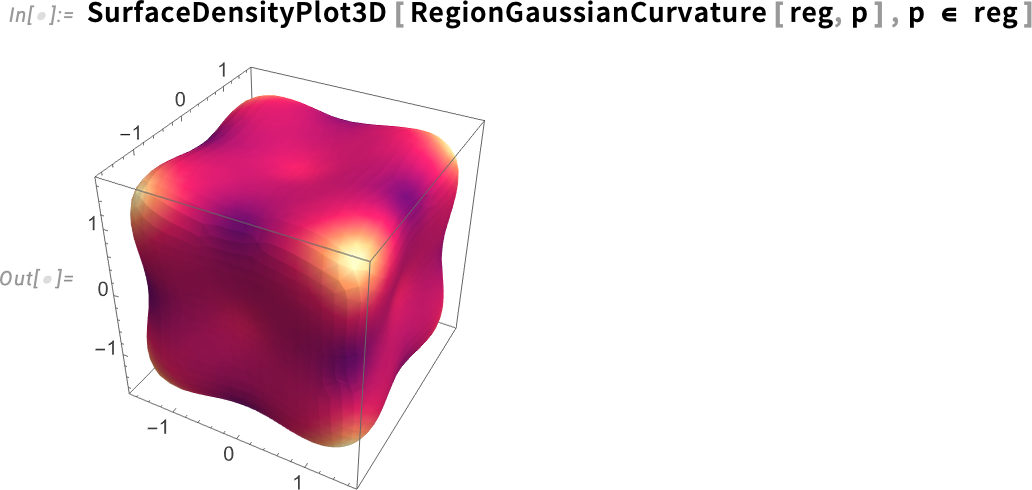
De most már pontos eredményeket is kaphatunk. Például ezzel meg tudunk találni egy pontot a felületen:

 

És ezzel aztán kiszámíthatjuk a Gauss-görbület pontos értékét azon a ponton:

 

A 14.3-as verzió emellett bevezeti a középgörbület (mean curvature) mérőszámokat a felületekhez.

 

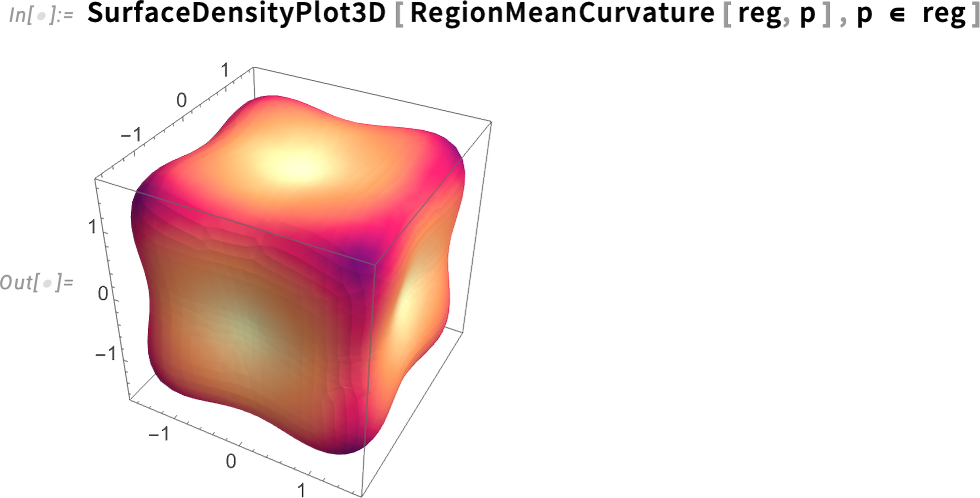
valamint a maximális és minimális görbületeket is:

 

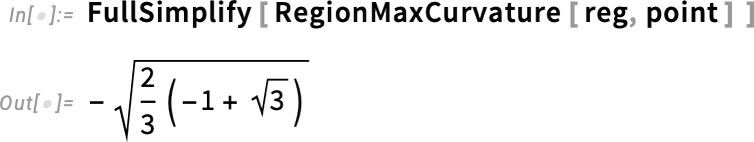
Ezek a felületi görbületek tulajdonképpen a 14.3-as verzióban bevezetett 3D-s általánosításai annak a ArcCurvature-nek, amelyet több mint egy évtizede, a 10.0-s verzióban mutattunk be: a minimális és maximális görbületek megfelelnek a felületre fektetett görbék minimális és maximális görbületeinek; a Gauss-görbület ezek szorzata, míg a középgörbület (mean curvature) az átlaguk.

 

 

 

 

Geodézia és útvonaltervezés

Mi a legrövidebb út két pont között — például egy felületen? A 14.3-as verzióban erre használhatjuk a FindShortestCurve függvényt. Példaként keressük meg a legrövidebb utat (vagyis a geodetikust) két pont között egy gömb felületén:

 

Igen, láthatunk egy kis ívet, ami egy nagykör egy szakaszának tűnik. De valójában szeretnénk ezt a gömbön is vizualizálni. Nos, ezt megtehetjük a HighlightRegion segítségével:

 

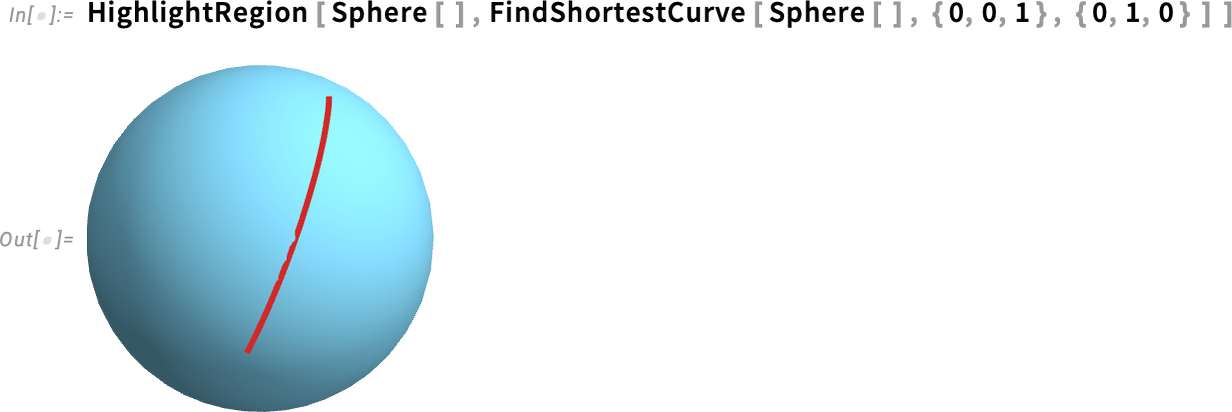
Íme egy hasonló eredmény egy tórusz esetében:

 

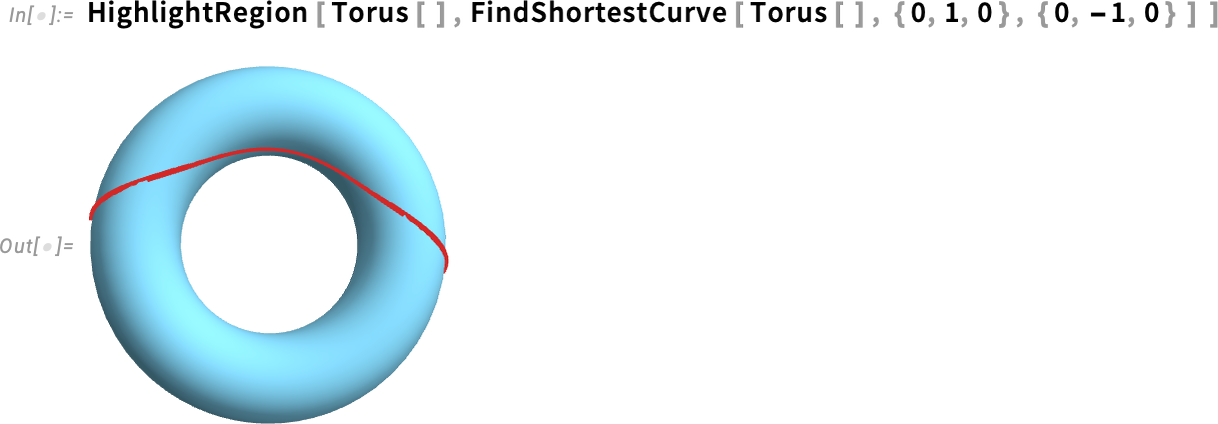
De valójában bármilyen régió működik. Például a Mars egyik holdja, a Phobos is:

 

Válasszunk két véletlenszerű pontot ezen:

 

Most pedig meg tudjuk találni a legrövidebb görbét e pontok között a felületen:

 

Használhatjuk az ArcLength függvényt a görbe hosszának meghatározására, vagy közvetlenül az új ShortestCurveDistance függvényt is:

 

Íme 25 geodetikus görbe véletlenszerű pontpárok között:

 

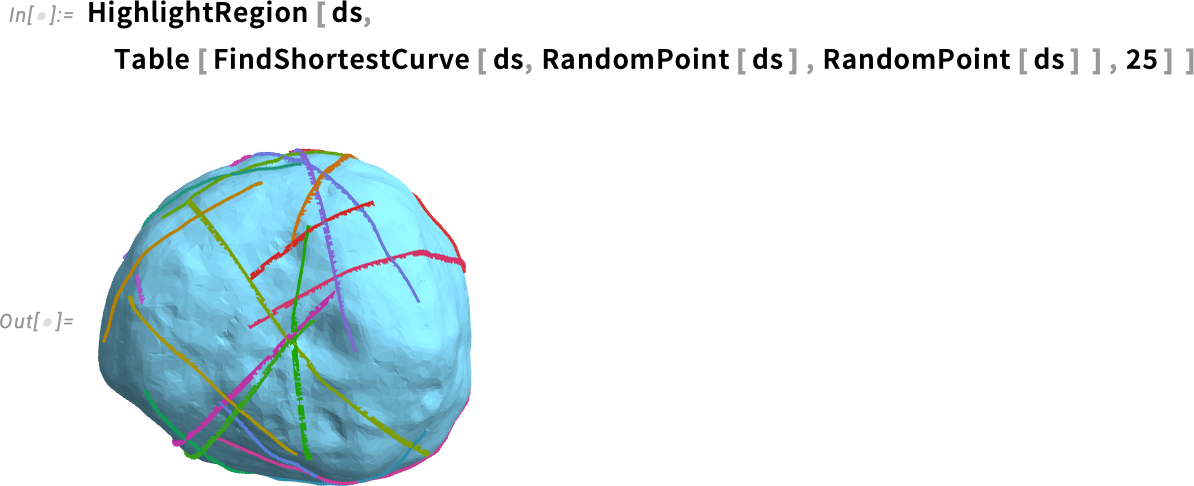
És igen, a régió lehet bonyolult; a FindShortestCurve ezt is képes kezelni. De nem véletlenül „Find…” (keres) függvény a neve: általánosságban ugyanis több, azonos hosszúságú út is létezhet.

 

Eddig 3D-beli felületeket vizsgáltunk. De a FindShortestCurve 2D-ben is működik:

 

És mire jó ez mindez? Nos, az egyik fontos alkalmazás az útvonaltervezés. Tegyük fel, hogy egy robotot szeretnénk eljuttatni innen oda, miközben el kell kerülnie az akadályokat stb. Mi a legrövidebb út, amelyet megtehet? Erre használhatjuk a FindShortestCurve függvényt. Ha pedig figyelembe szeretnénk venni a „robot méretét”, azt úgy tehetjük meg, hogy „megnöveljük (dilatáljuk) az akadályokat”. Így például itt látható egy elrendezési terv néhány bútorral:

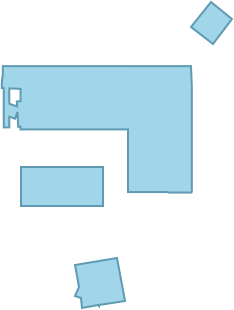
Most „dilatáljuk” ezt, hogy megkapjuk az effektív régiót egy 0,8 sugarú robot számára:

 

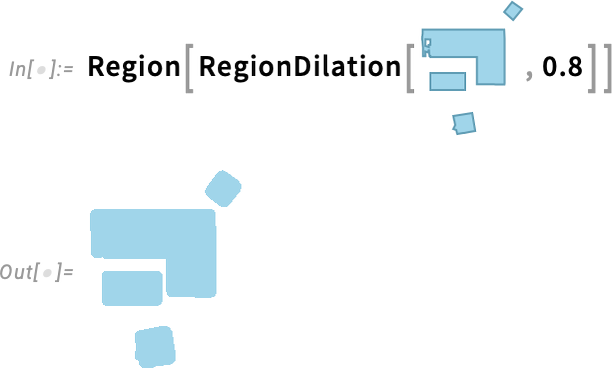
Ha ezt most egy „szőnyeghez” viszonyítva invertáljuk, megkapjuk azt az effektív régiót, amelyben a robot (pontosabban a robot középpontja) mozoghat:

 

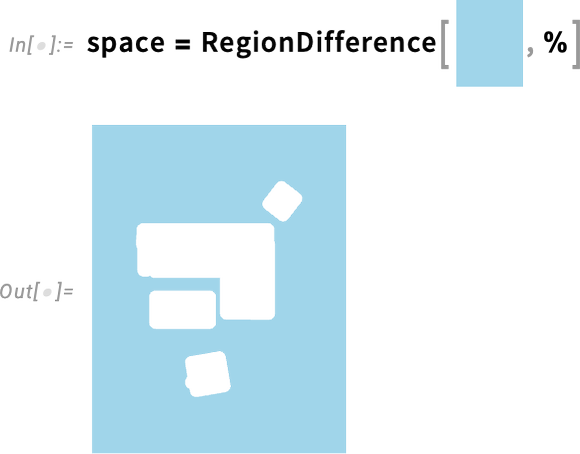
Most már a FindShortestCurve segítségével megkereshetjük a legrövidebb útvonalakat, amelyeken a robot eljuthat a különböző célpontokhoz.

 

 

 

 

 

Geometria az alrészből

„Realisztikus” geometria létrehozása nehéz feladat, különösen 3D-ben. Ennek megkönnyítésére az egyik módszer az, hogy az elképzelt alakzatot alapvető testek (például gömbök, hengerek stb.) kombinálásával építjük fel. Az ilyen jellegű „konstruktív geometriát” már a 13.0-s verzió óta támogatjuk. A 14.3-as verzióban azonban megjelent egy másik, rendkívül hatékony alternatíva: abból indulunk ki, hogy van egy „váz” (skeleton) az elképzelt alakzathoz, majd ezt úgy töltjük ki, hogy egy végtelen sok felosztás (subdivision) határát vesszük. Így például indulhatunk egy nagyon durva, lapos felületekből álló közelítésből egy tehén geometriájára, és az ismételt felosztások révén fokozatosan egy sima alakzattá alakíthatjuk:

 

Elég tipikus, hogy valami „matematikai jellegűből” indulunk ki, és végül valami sokkal „természetesebb” vagy „biológiaibb” formához jutunk.

 

Íme, mi történik, ha egy kockából indulunk ki, majd egymás után többször felosztjuk (szubdividáljuk) minden egyes lapját:

 

Egy élethűbb példaként tegyük fel, hogy egy csont közelítő hálójával (mesh) indulunk:

 

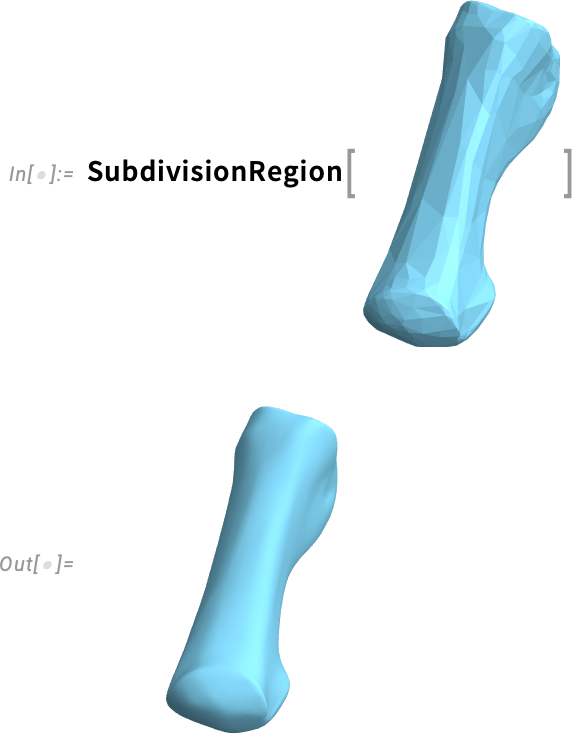
A SubdivisionRegion azonnal egy simított — és feltehetően élethűbb — változatot ad. Ahogy a Wolfram Language többi számítási geometriája, a SubdivisionRegion nemcsak 3D-ben működik, hanem 2D-ben is. Például készíthetünk egy véletlenszerű Voronoi-hálót:

 

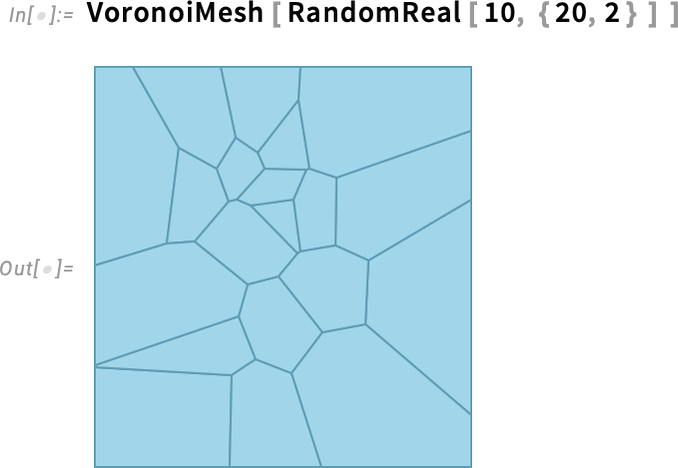
majd feloszthatjuk poligonális cellákra:

 

és ezután ezekből SubdivisionRegion-öket készíthetünk, hogy egy kifejezetten „kavicsos” hatást érjünk el:

 

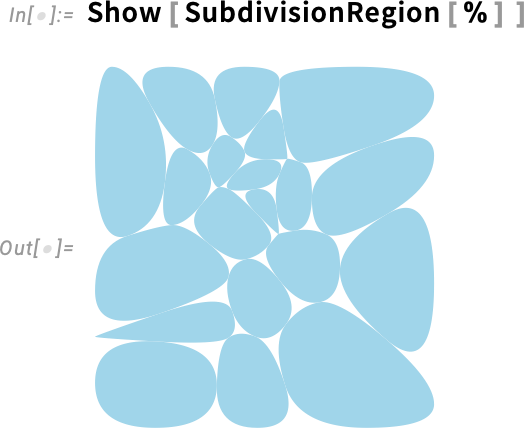
Vagy 3D-ben:

 

 

 

 

 

Javítsd meg a hálót!

Tegyük fel, hogy van egy 3D pontfelhőnk, például egy szkennerből származó adatok:

 

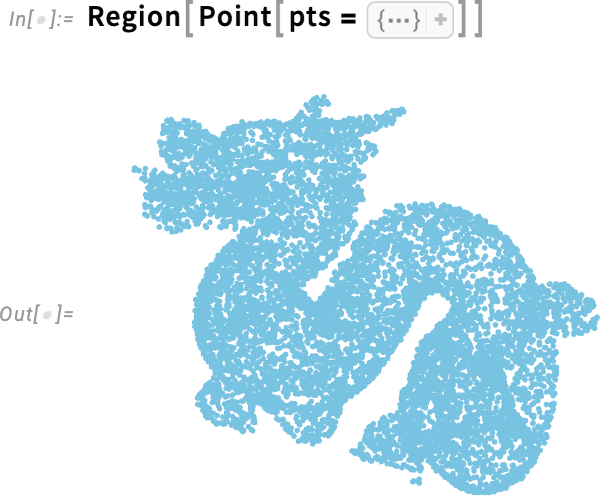
A ReconstructionMesh függvény, amelyet a 13.1-es verzióban vezettünk be, megpróbál egy felületet rekonstruálni ebből a pontfelhőből:

 

Elég gyakori, hogy az ilyen pontfelhők „zajos”, gyűrött” felületet adnak. A 14.3-as verzióban azonban már van egy új függvény, amellyel ezt simíthatjuk:

 

Ez szép eredmény. Ugyanakkor sok poligon van benne, és bizonyos számításokhoz egyszerűbb hálóra, kevesebb poligonra lehet szükség. Az új SimplifyMesh függvény bármely hálót át tud alakítani úgy, hogy kevesebb poligonnal közelítő hálót kapjunk:

 

És igen, kicsit „laposabbnak” tűnik, de a poligonok száma tízszer kevesebb lett:

 

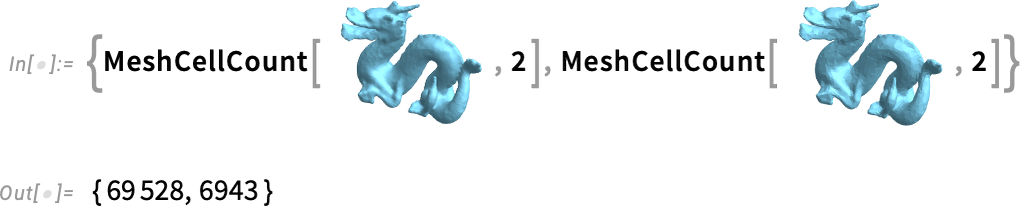
Egyébként a 14.3-as verzióban egy másik új függvény is megjelent: Remesh. Amikor hálókon végzünk műveleteket, elég gyakori, hogy a hálóban „furcsa” (például nagyon hegyes) poligonok keletkeznek. Ilyen poligonok problémát okozhatnak például 3D nyomtatásnál vagy véges elemes analízisnél. A Remesh létrehoz egy új, „újracsomagolt” hálót, amelyben az ilyen furcsa poligonokat elkerüli.

 

 

 

 

Színezd ki azt a molekulát – és még sok más

A kémiai számítások a Wolfram Language-ben komolyabban hat éve, a 12.0-s verzióban indultak el, a Molecule és a hozzá kapcsolódó számos függvény bevezetésével. Azóta energikusan bővítettük a nyelv kémiai funkcionalitását.

A 14.3-as verzióban egy új lehetőség a molekulák vizualizálása, amelyben az atomok vagy a kötések színe tulajdonságértékeket jeleníthet meg. Például az alábbi ábrán a koffein molekulában az atomok oxidációs állapotai láthatók:

 

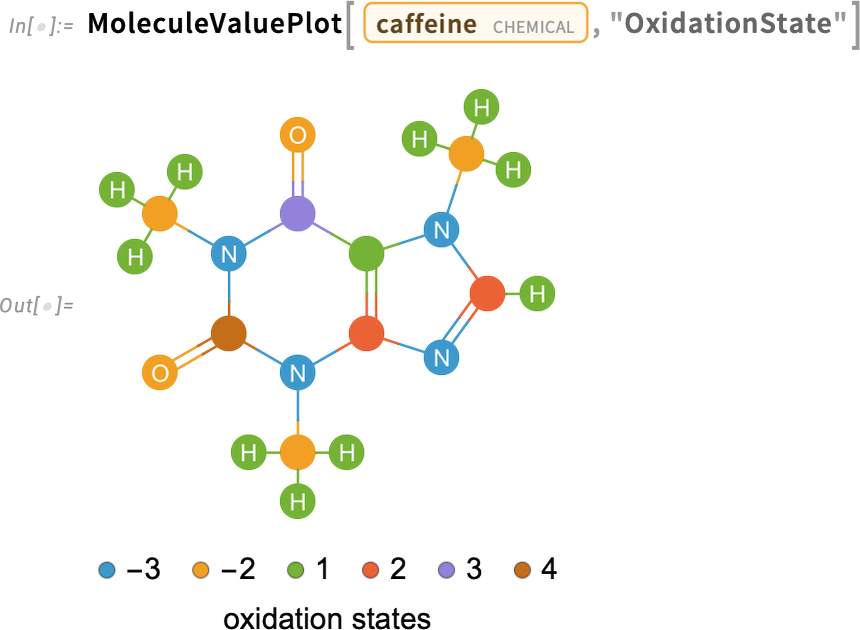
És íme egy 3D-s változat:

 

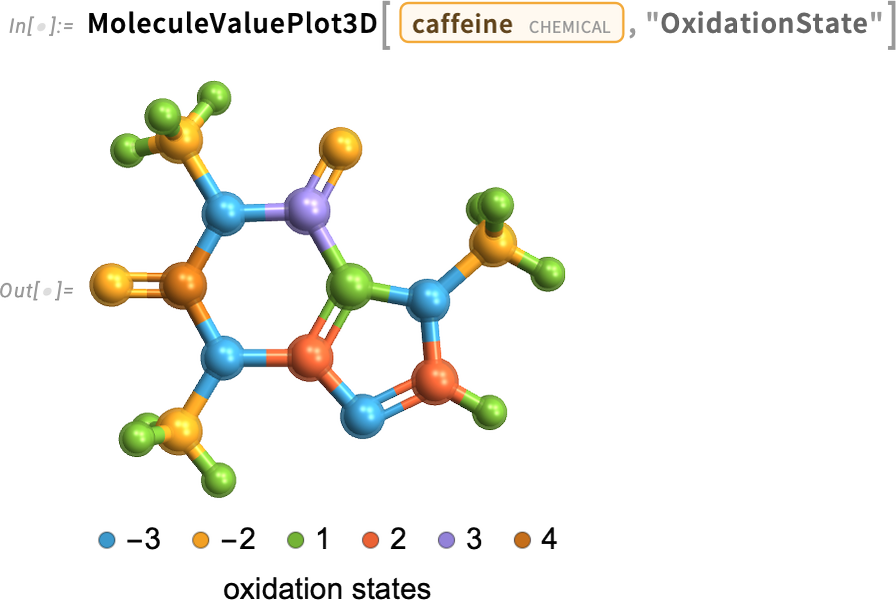
És itt egy példa, ahol a színezéshez használt mennyiség folyamatos értéktartományú:

 

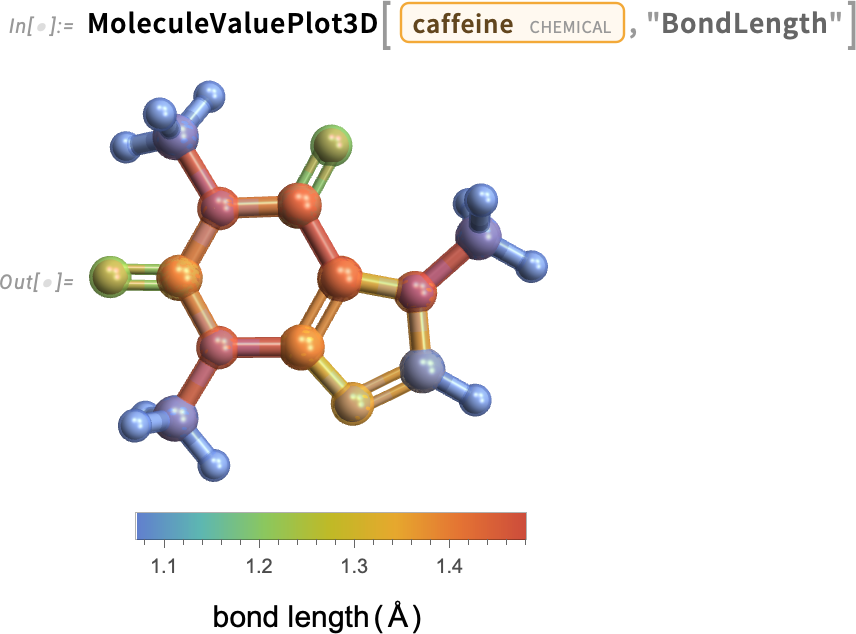
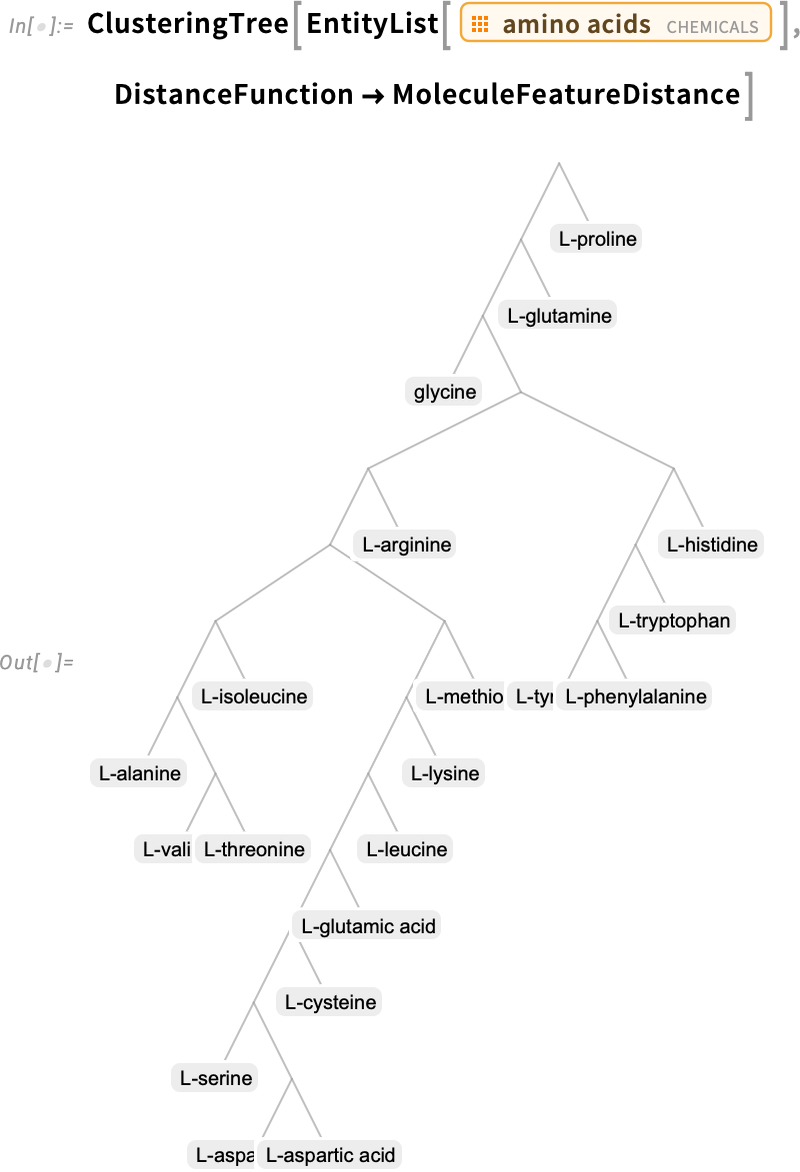
A 14.3-as verzióban egy másik új kémiai függvény a MoleculeFeatureDistance, amely kvantitatív módot ad arra, hogy megmérjük, mennyire hasonlít két molekula egymáshoz:

 

Ezt a távolságot például felhasználhatjuk molekulák klaszterező fájának elkészítésére; itt például aminosavak esetén:

 

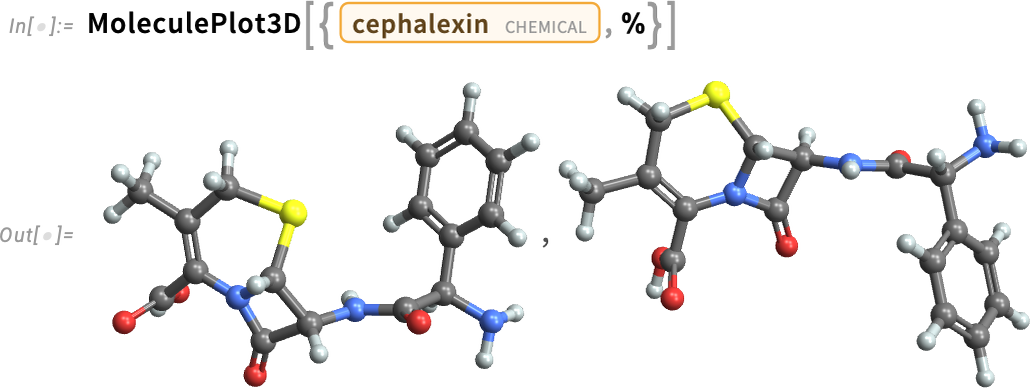
Amikor először bevezettük a Molecule-t, egyúttal a MoleculeModify-t is bemutattuk. Az évek során folyamatosan bővítettük a MoleculeModify funkcionalitását. A 14.3-as verzióban hozzáadtuk a lehetőséget, hogy megfordítsuk egy molekula szerkezetét egy adott atom körül, lényegében megfordítva a molekula lokális sztereokémiáját:

 

 

 

 

 

 

A fehérjék lokálisan hajtogatódnak

Milyen alakja lesz annak a fehérjének? A Wolfram Language hozzáfér egy nagy adatbázishoz, amely olyan fehérjéket tartalmaz, amelyek szerkezetét kísérletileg már meghatározták. De mi a helyzet akkor, ha egy új, eltérő aminosav-szekvenciával dolgozunk? Hogyan fog feltekeredni (foldolódni)? A 14.1-es verzió óta a BioMolecule automatikusan megpróbálja meghatározni ezt, azonban ehhez egy külső API-t kellett meghívnia. A 14.3-as verzióban viszont már úgy állítottuk be a rendszert, hogy a fehérje-foldolást helyben, a saját számítógépeden is el tudd végezni. A szükséges neurális háló nem kicsi — körülbelül 11 GB letöltést igényel, és kicsomagolva 30 GB helyet foglal a számítógépen. Azonban az, hogy teljes mértékben helyben dolgozhatunk, lehetővé teszi a fehérje-foldolás szisztematikus elvégzését, külső API-k mennyiségi és sebességkorlátai nélkül.

Íme egy példa a helyi fehérje-foldolásra:

 

És ne felejtsük el: ez csupán egy gépi tanuláson alapuló becslés a szerkezetre. Íme ebben az esetben a kísérletileg mért szerkezet — minőségileg hasonló, de nem teljesen azonos:

 

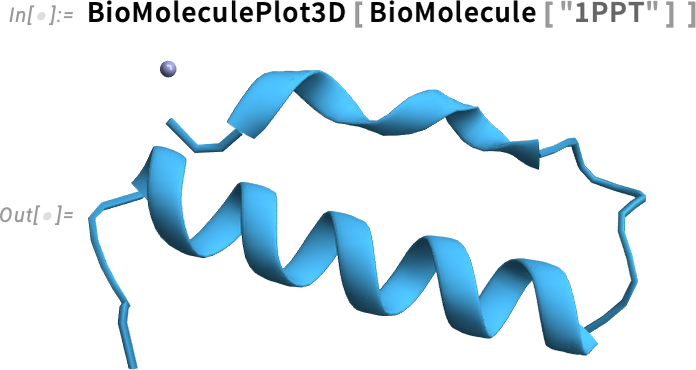
De hogyan tudjuk ezeket a szerkezeteket ténylegesen összehasonlítani? Nos, a 14.3-as verzióban megjelent egy új függvény, a BioMoleculeAlign (a MoleculeAlign analógiája), amely megpróbálja az egyik biomolekulát a másikhoz igazítani. Íme ismét az általunk előre jelzett feltekeredés:

 

Most pedig illesztjük (igazítjuk) a kísérleti szerkezetet ehhez:

 

Ez most együtt jeleníti meg a szerkezeteket:

 

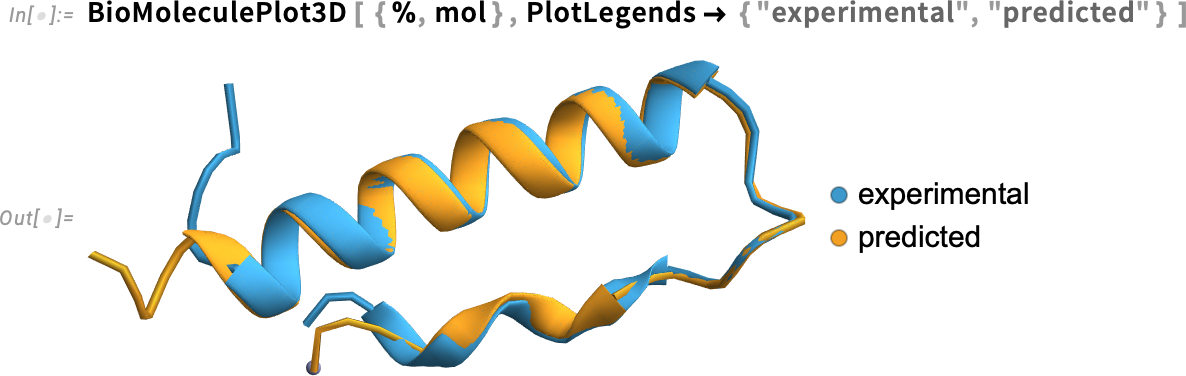
És igen, legalábbis ebben az esetben az egyezés meglehetősen jó, és például a hiba (a gerincben lévő központi szénatomokra átlagolva) kicsi.

 

A 14.3-as verzió néhány új kvantitatív mérőszámot is bevezet a „fehérjealak” jellemzésére. Először is ott vannak a Ramachandran-szögek, amelyek a fehérje gerincének „csavarodását” mérik (és igen, ez a két elkülönülő tartomány megfelel azoknak a különálló régióknak, amelyeket a fehérjén vizuálisan is megfigyelhetünk).

 

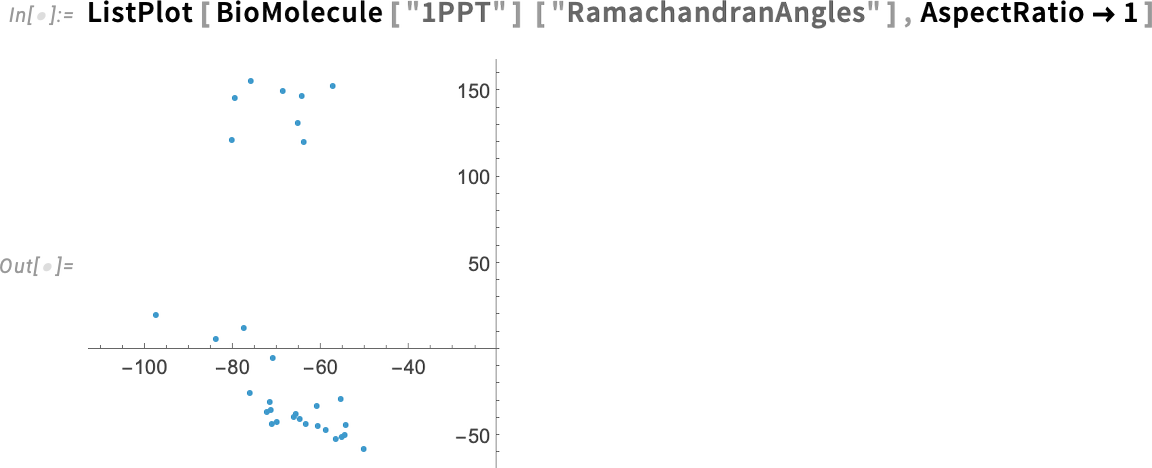
Ezután ott van a távolságmátrix is, amely a fehérjében található összes reziduum (vagyis aminosav) közötti távolságokat tartalmazza:

 

 

 

 

 

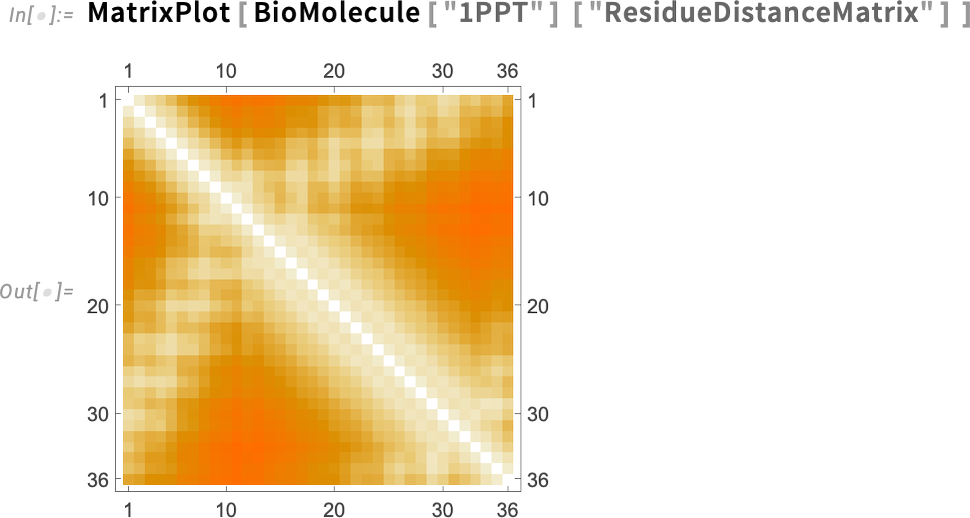
Vajon ez a mérnöki rendszer tényleg működni fog?

Több mint egy évtizede a Wolfram System Modeler lehetővé teszi valós mérnöki és egyéb rendszerek modelljeinek felépítését és szimulációját. A „valós világ” alatt egyre bővülő körű tényleges rendszereket értek — valódi autókat, repülőgépeket, erőműveket stb. — több tízezer alkatrésszel, amelyeket vállalatok hoztak létre (nem is beszélve a biomedicinális rendszerekről stb.). A tipikus munkafolyamat során a rendszereket interaktívan építjük fel a System Modelerben, majd a Wolfram Language segítségével végezzük el rajtuk az elemzést, az algoritmikus tervezést és egyéb feladatokat. Most pedig, a 14.3-as verzióban, egy jelentős új képességgel bővült a rendszer: a rendszerek validálása is elvégezhető közvetlenül a Wolfram Language-ben.

A rendszer a számára meghatározott határértékeken belül marad majd? Biztonsági, teljesítménybeli és egyéb okokból ez gyakran nagyon fontos kérdés. Most pedig ez egy olyan kérdés, amelyre a SystemModelValidate segítségével választ kaphatunk. De hogyan adjuk meg a követelményeket? Ehhez néhány új függvényre van szükség. Ilyen például a SystemModelAlways, amellyel megadhatunk egy feltételt, amelynek a rendszernek mindig meg kell felelnie. Vagy a SystemModelEventually, amellyel olyan feltételt adhatunk meg, amelynek a rendszernek idővel meg kell felelnie.

Kezdjük egy egyszerű, szemléltető példával. Tekintsük a következő differenciálegyenletet:

 

Oldjuk meg ezt a differenciálegyenletet, és az eredmény:

 

Ezt felállíthatjuk System Modeler-stílusú modellként:

 

Ez szimulálja a rendszert, és ábrázolja a viselkedését:

 

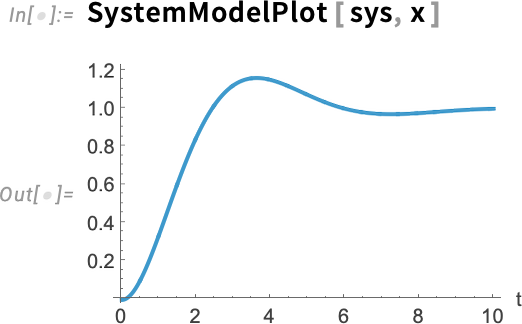
Most tegyük fel, hogy ellenőrizni szeretnénk a rendszer viselkedését, például azt, hogy túllépi-e valaha az 1,1 értéket. Ekkor csak annyit kell mondanunk:

 

És igen, ahogy az ábra is mutatja, a rendszer nem mindig teljesíti ezt a feltételt. Íme, hol bukik meg:

 

És itt látható a meghibásodás régiójának vizuális ábrázolása:

 

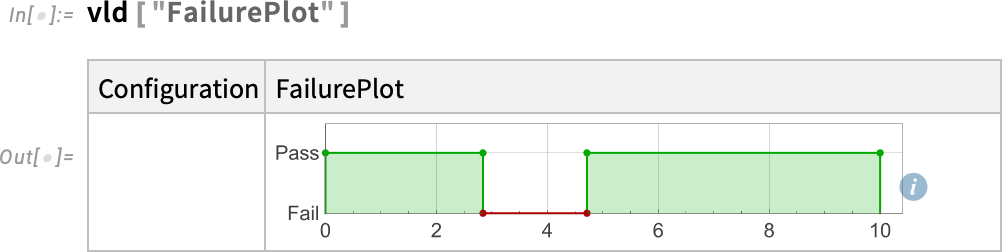
Rendben, nézzünk egy reálisabb példát. Itt egy kissé egyszerűsített modell az elektromos autó hajtásláncáról (469 rendszerbeli változóval):

 

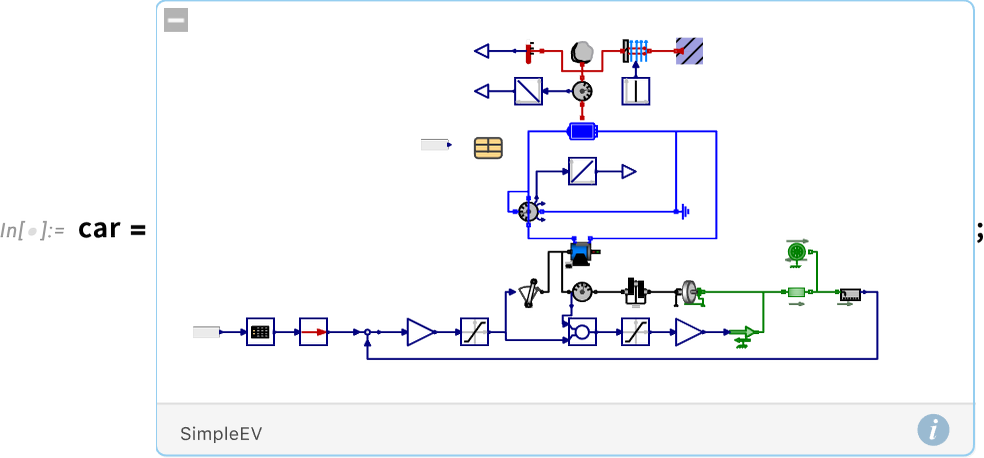
Tegyük fel, hogy a követelményünk a következő: „Az USA EPA Highway Fuel Economy Driving Schedule (HWFET) szerint az autó akkumulátorának hőmérséklete legfeljebb 10 percig lehet 301 K fölött.” A modell felállításakor már beillesztettük a HWFET „bemeneti adatokat”. Most a követelmény többi részét szimbolikus formába kell átültetnünk. Ehhez szükség van egy időbeli logikai konstrukcióra, amely szintén újdonság a 14.3-as verzióban: SystemModelSustain. Végül ezt mondjuk ki: „Ellenőrizzük, hogy mindig igaz-e, hogy a hőmérséklet nem marad 10 percig vagy tovább 301 K fölött.” Most már futtathatjuk a SystemModelValidate-et, hogy megtudjuk, igaz-e ez a modellünkre.

 

És nem, nem teljesül. De hol hibázik a rendszer? Ezt ábrázolhatjuk egy grafikonon:

 

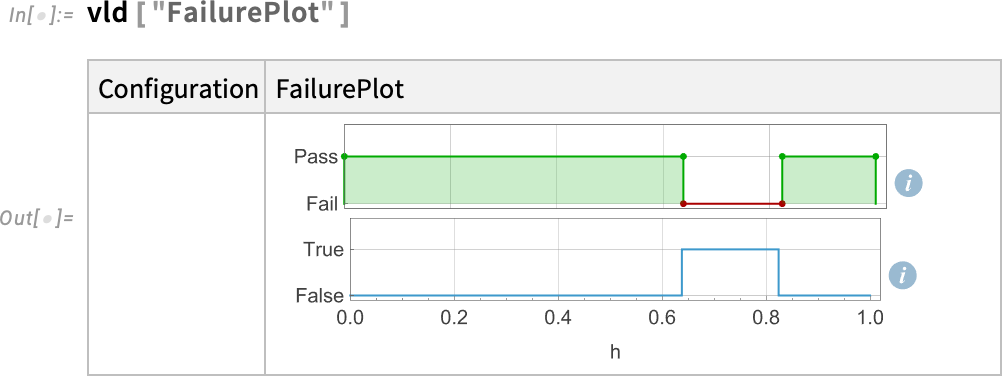
A modell szimulálásával láthatjuk a meghibásodást:

 

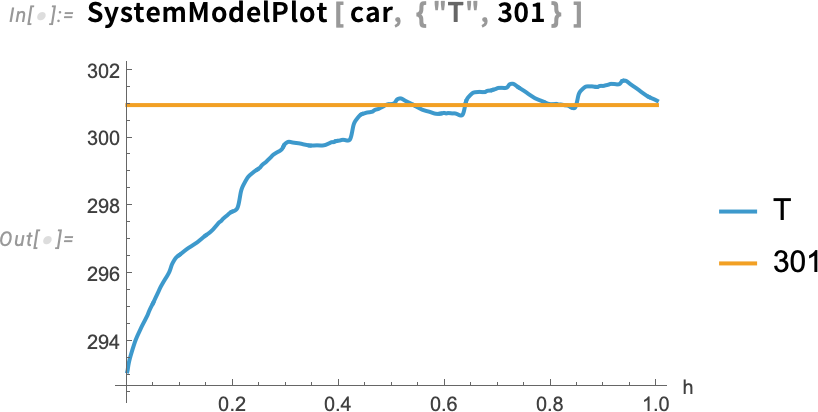
Itt rengeteg technológia van a háttérben. Mindez teljesen ipari méretekre van felkészítve, így bármilyen valós rendszerre alkalmazhatod, amelyhez rendelkezel rendszermodellel.

 

 

 

 

Vezérlőrendszer-munkafolyamataink gördülékenyebbé tétele

Ez egy olyan képesség, amelyet az elmúlt 15 évben folyamatosan építettünk: a szabályozórendszerek tervezésének és elemzésének lehetőségét. Ez egy összetett terület, ahol egy adott szabályozórendszert sokféleképpen lehet vizsgálni, és sokféle feladatot lehet vele elvégezni. A szabályozórendszer-tervezés jellemzően erősen iteratív folyamat, amelyben a tervet újra és újra finomítjuk, amíg minden tervezési követelmény teljesül.

A 14.3-as verzióban ezt jelentősen megkönnyítettük: könnyű hozzáférést biztosítunk nagymértékben automatizált eszközökhöz, valamint a rendszer többféle nézetéhez.

Íme egy példa egy rendszer modelljére (a szabályozástechnika nyelvén egy „plant modell”), nemlineáris állapottér-formában megadva:

 

Ez a modell történetesen egy rugalmas ingát ír le:

 

A 14.3-as verzióban most már rákattinthatsz a modell notebookban megjelenített reprezentációjára, és megjelenik egy „szalagmenü” (ribbon), amely például lehetővé teszi a modell megjelenítési formájának megváltoztatását:

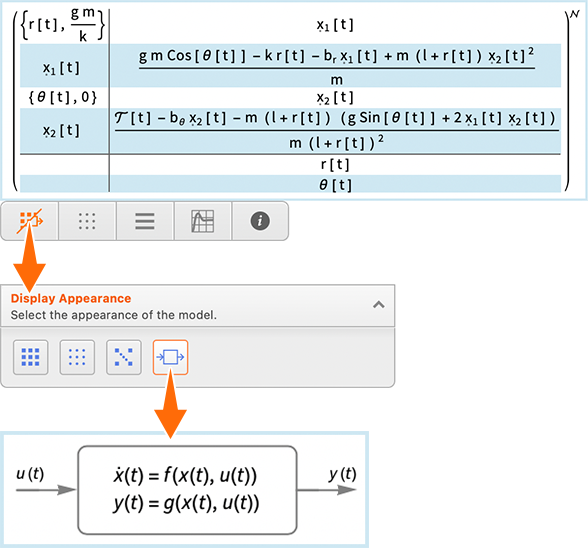
Ha a modell összes paraméteréhez numerikus értékeket adtál meg

 

akkor azonnal elvégezhetsz olyan műveleteket is, mint például a szimulációs eredmények lekérése:

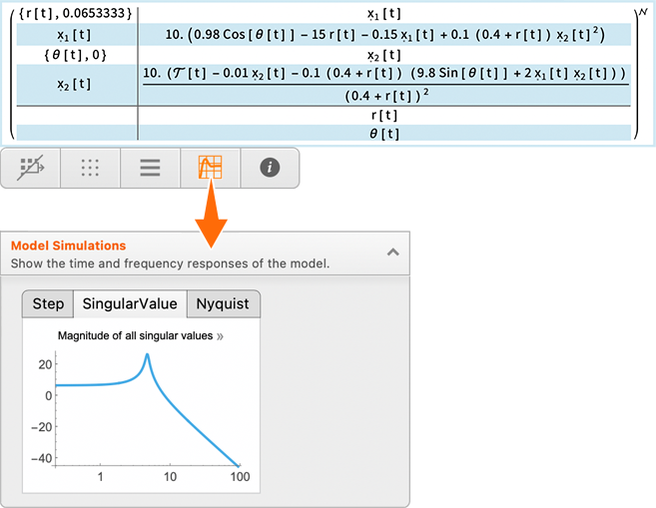
Rákattintva az eredményre közvetlenül kimásolhatod a kódot, amellyel az eredmény előállítható:

 

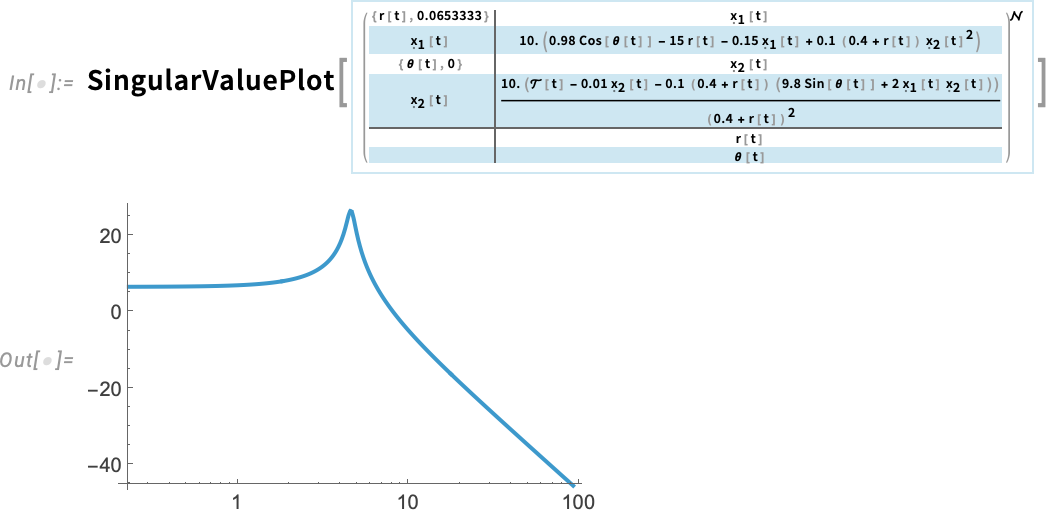
Számos tulajdonságot kinyerhetünk az eredeti állapottér-modellből. Például itt láthatók a rendszer differenciálegyenletei, amelyek közvetlenül alkalmasak az NDSolve bemeneteként való használatra:

 

Egy iparibb jellegű példaként tekintsünk egy adott típusú helikopter állásszög- (pitch) dinamikájának linearizált modelljére:

 

Ebben az esetben az állapottér-modell ilyen alakú (és egy üzemi pont körül linearizált, így ez csupán a lineáris differenciálegyenletek együtthatóit tartalmazó mátrixokat adja meg):

 

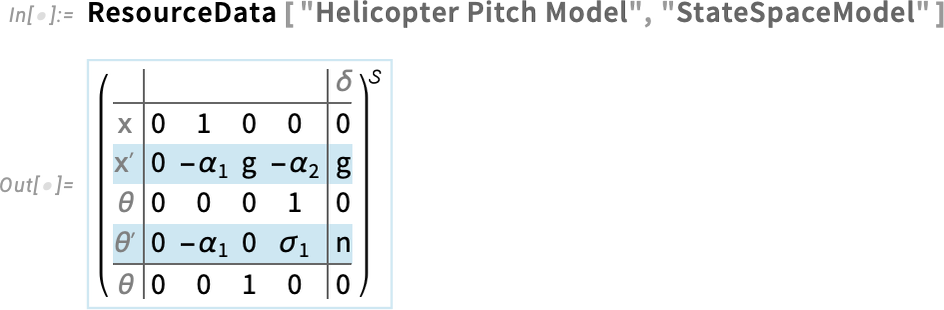
Íme a modell, amelybe már be lettek helyettesítve a numerikus értékek:

 

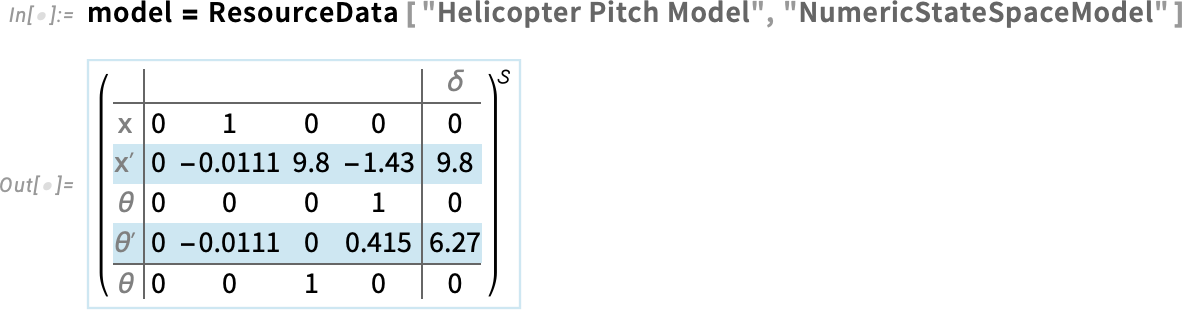
De hogyan viselkedik ez a modell? Egy gyors áttekintéshez használhatod az új PoleZeroPlot függvényt a 14.3-as verzióban, amely megjeleníti a sarkok (sajátértékek) és nullák helyzetét a komplex síkon:

 

Ha ismered a szabályozórendszereket, azonnal észreveszed a jobboldali fél síkban lévő sarkokat, ami azt jelzi, hogy a jelenlegi beállításokkal a rendszer instabil.

Hogyan lehetne stabilizálni? Ez a szabályozórendszer-tervezés tipikus célja. Példaként itt keressünk egy LQ-vezérlőt ehhez a rendszerhez — a célokat a következőképpen megadott súlyozó mátrixokkal határozzuk meg:

 

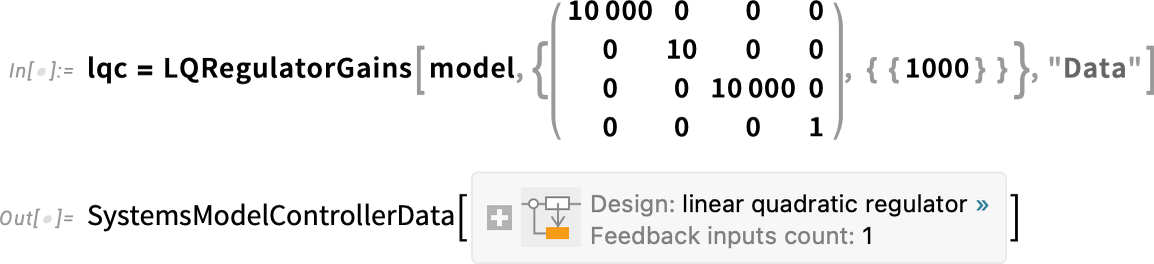
Most ábrázolhatjuk (narancssárgával) a vezérlővel ellátott rendszer sarkait, együtt a kék színnel a eredeti, nem szabályozott rendszer sarkaival:

 

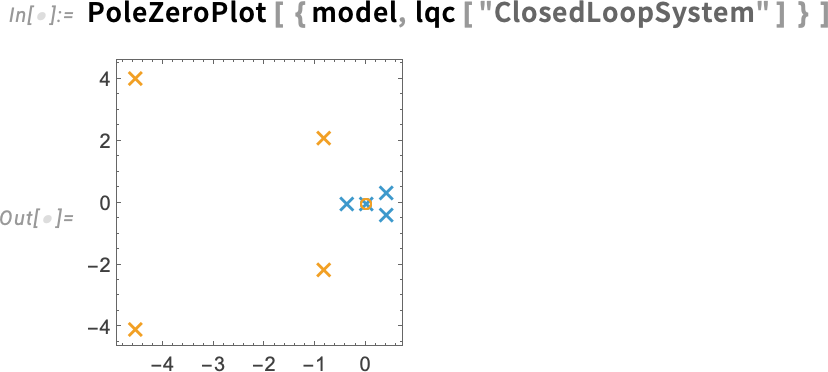
És látjuk, hogy igen, a kiszámított vezérlő valóban stabilizálja a rendszerünket.

De mit csinál valójában a rendszer? Lekérhetjük a rendszer válaszát adott kezdeti feltételek mellett (itt például, hogy a helikopter kicsit felfelé dőlt):

 

Az ábrázolásból látható, hogy igen, a helikopter először kicsit himbálózik, majd végül stabilizálódik:

 

 

 

 

 

Hiperbolikus megközelítés a grafikon elrendezésében

Hogyan érdemes elrendezni egy fát? Viszonylag kisméretű esetekben lehetséges, hogy botanikai fa módjára nézzen ki, bár a gyökér a tetején legyen:

 

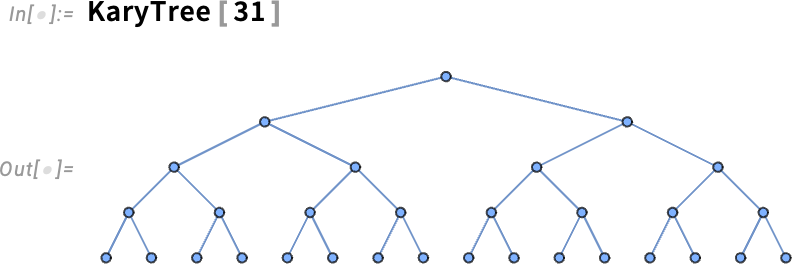
Nagyobb esetekben már nem olyan egyértelmű, mit tegyünk. Alapértelmezés szerint ilyenkor egyszerűen a általános gráfelrendezési technikákhoz fordulunk:

 

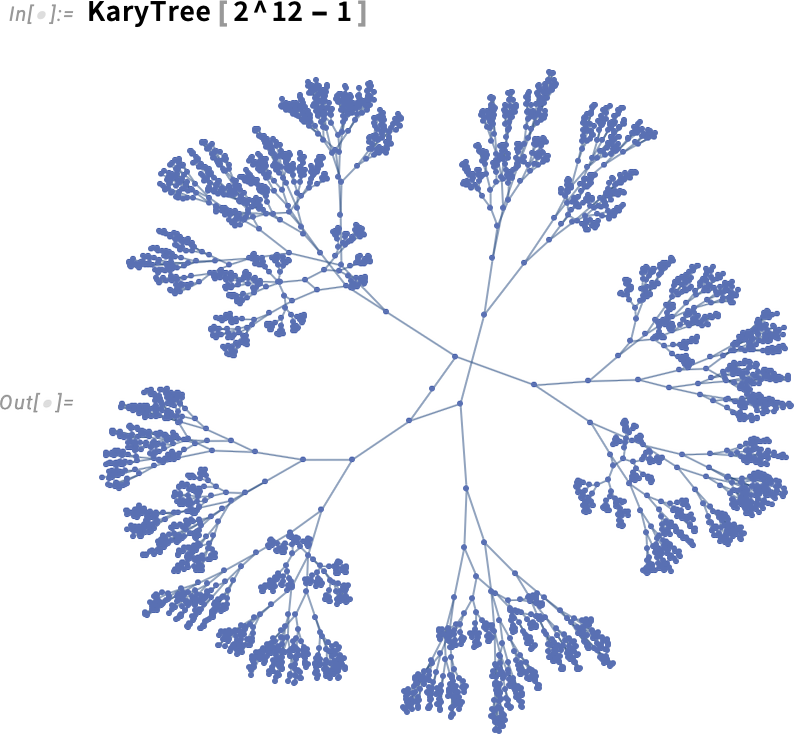
De a 14.3-as verzióban van egy elegánsabb megoldás is: a gráfot gyakorlatilag hiperbolikus térben helyezhetjük el:

 

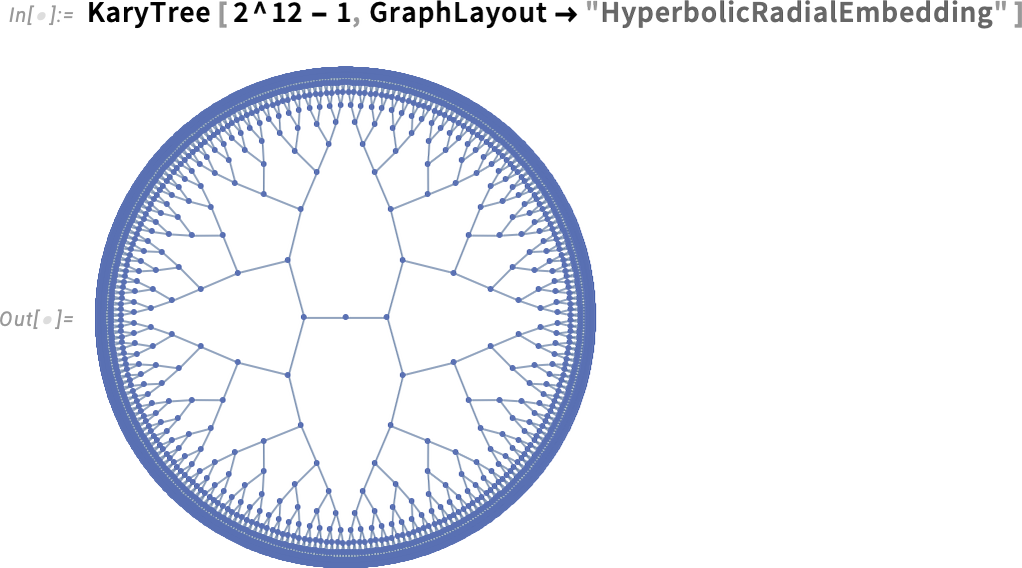
A “HyperbolicRadialEmbedding” esetén gyakorlatilag a fa minden ága radiálisan terjed ki a hiperbolikus térben. Általánosságban azonban előfordulhat, hogy egyszerűen csak a hiperbolikus térben szeretnénk működni, miközben a gráf éleit rugóként kezeljük. Íme egy példa arra, mi történik ilyen esetben:

 

Matematikai szinten a hiperbolikus tér végtelen. A gráfelrendezések során azonban ezt a Poincaré-diszk koordináta-rendszerébe vetítjük. Általánosságban szükséges kiválasztani a koordináta-rendszer origóját, vagy gyakorlatilag a gráf „gyökércsúcsát”, amely a Poincaré-diszk közepén lesz megjelenítve:

 

 

 

 

 

Das Neueste in der Analysis: Hilbert-Transformationen, Lommel-Funktionen

Elvégeztük a Laplace-, Fourier-, Mellin-, Hankel- és Radon-transzformációkat. Ezek mind integráltranszformációk. És most, a 14.3-as verzióban, elérkeztünk a legutolsóhoz (és egyben a legnehezebbhez) a gyakori integráltranszformációk közül: a Hilbert-transzformációhoz. A Hilbert-transzformációk gyakran felbukkannak, amikor jelekkel és hasonló objektumokkal foglalkozunk. Megfelelő felállás esetén ugyanis a Hilbert-transzformáció lényegében egy jel valós részét — például a frekvencia függvényében — veszi, és (feltételezve, hogy jól viselkedő analitikus függvénnyel van dolgunk) megadja annak képzetes részét.

Egy klasszikus példa (optikában, szóráselméletben stb.) a következő:

 

 

 

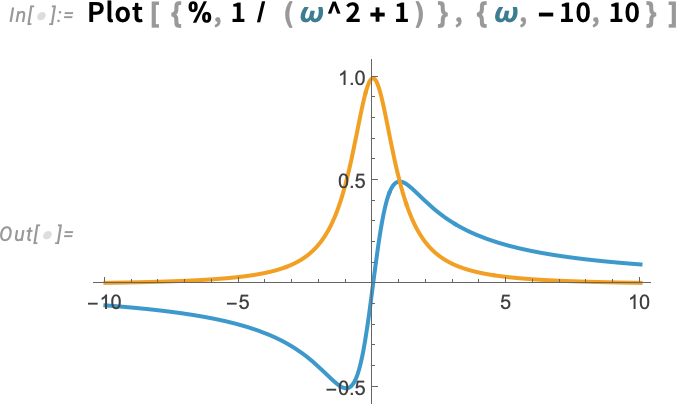
Mondanunk sem kell, hogy a HilbertTransform függvényünk gyakorlatilag bármilyen Hilbert-transzformációt képes elvégezni, amely szimbolikusan elvégezhető.

 

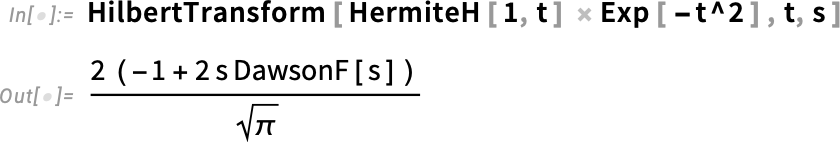
És igen, ez egy meglehetősen egzotikus speciális függvényt eredményez, amelyet még a 7.0-s verzióban adtunk hozzá.

És ha már a speciális függvényeknél tartunk: sok korábbi verzióhoz hasonlóan a 14.3-as verzió is további speciális függvényekkel bővül. És igen, közel négy évtized után határozottan kezdünk kifogyni a hozzáadható speciális függvényekből — legalábbis az egy-változós esetben. A 14.3-as verzióban azonban még van egy utolsó csoport: a Lommel-függvények. A Lommel-függvények az inhomogén Bessel-féle differenciálegyenlet megoldásai:

 

Négy változatban léteznek — LommelS1, LommelS2, LommelT1 és LommelT2:

 

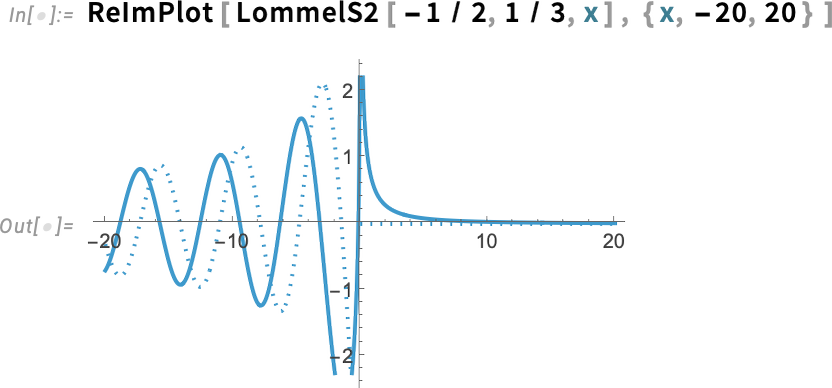
És igen, a komplex sík bármely pontján kiértékelhetők, tetszőleges pontossággal.

 

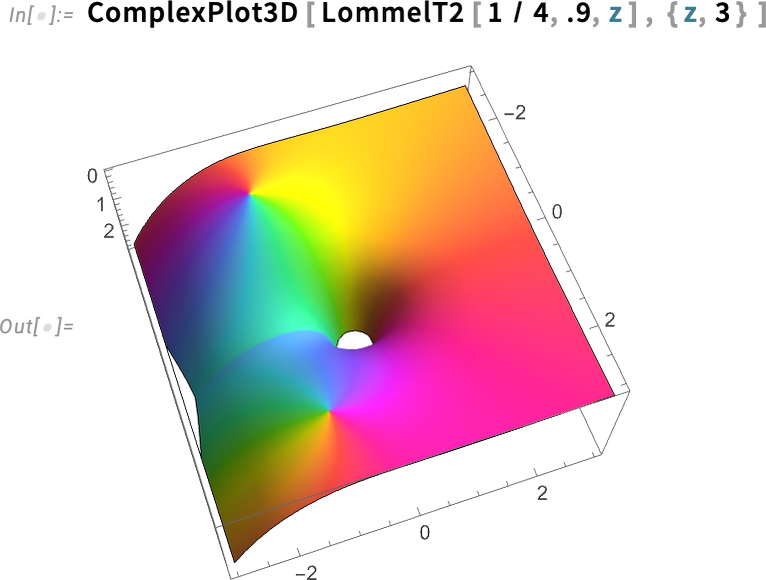
A Lommel-függvények és más speciális függvények között mindenféle összefüggés és kapcsolat létezik:

 

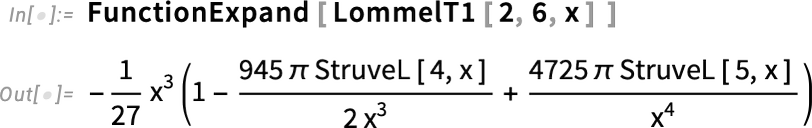
És igen, ahogyan a többi speciális függvényünknél is, gondoskodtunk arról, hogy a Lommel-függvények a rendszer egészében megfelelően működjenek.

 

 

 

 

 

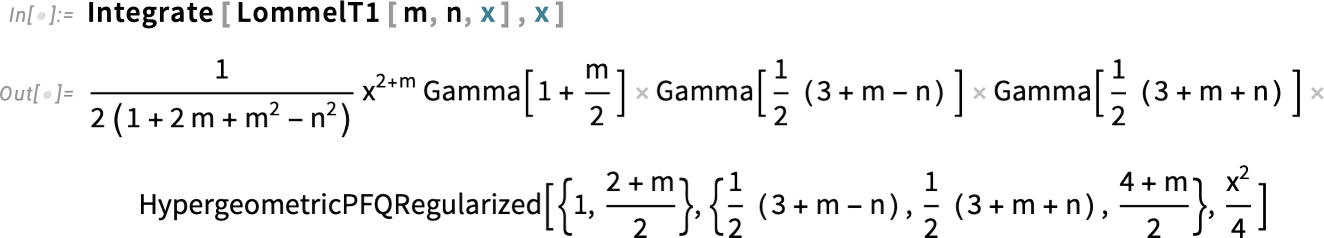
Több kitöltése a mátrixok világában

A mátrixok mindenütt megjelennek. Már a 1.0-s verziótól kezdve számos hatékony eszközzel rendelkeztünk a kezelésükre — numerikusan és szimbolikusan egyaránt. De — némileg a speciális függvényekhez hasonlóan — mindig vannak még feltáratlan területek. Ezért a 14.3-as verziótól kezdve nagyobb hangsúlyt fektetünk arra, hogy kibővítsük és egységesebbé tegyük mindazt, amit a mátrixokkal végzünk.

Íme egy meglehetősen egyszerű példa. Már az 1.0-s verzióban is létezett a NullSpace. Most pedig, a 14.3-as verzióban, hozzáadjuk a RangeSpace függvényt, amely a részterek egy kiegészítő reprezentációját adja. Például itt látható egy mátrix egydimenziós nulltere:

 

És itt látható ugyanennek a mátrixnak a megfelelő, 2 (= 3 – 1) dimenziós képtére (range space):

 

Mi van akkor, ha egy vektort erre a részterére szeretnél vetíteni? A 14.3-as verzióban kibővítettük a Projection függvényt, így már nemcsak egy vektorra, hanem egy altérre (részterére) is lehet vetíteni.

 

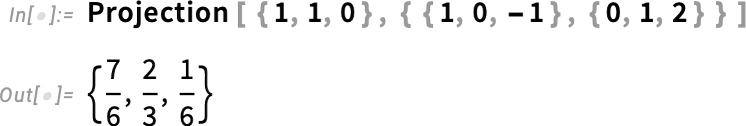
Mindezek a függvények nemcsak numerikusan, hanem — különböző módszerekkel — szimbolikusan is működnek.

 

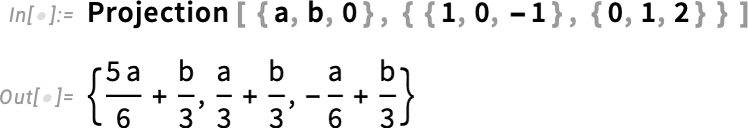
Az új képességek egy tartalmasabb csoportja a mátrixfelbontásokhoz (dekompozíciókhoz) kapcsolódik. A mátrixfelbontás alapötlete az, hogy kiemeljük azt a központi műveletet, amely egy adott mátrixalkalmazási osztályhoz szükséges. Már az 1.0-s verzióban is rendelkeztünk több mátrixfelbontással, és az évek során még jó néhányat hozzáadtunk. Most pedig, a 14.3-as verzióban, négy új mátrixfelbontást vezetünk be.

Az első az EigenvalueDecomposition, amely lényegében a mátrix sajátértékeinek és sajátvektorainak újracsomagolása, úgy kialakítva, hogy egy hasonlósági transzformációt definiáljon, amely diagonalizálja a mátrixot:

 

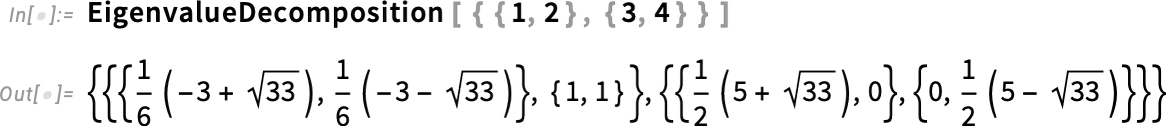
A következő új mátrixfelbontás a 14.3-as verzióban a FrobeniusDecomposition:

 

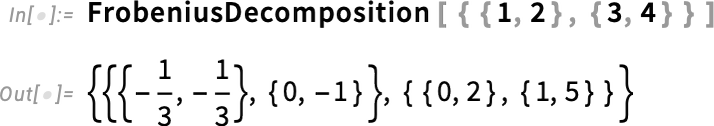
A Frobenius-felbontás lényegében ugyanazt a célt valósítja meg, mint a sajátérték-felbontás, de robosztusabb módon: például nem akad el degenerációk esetén, és elkerüli, hogy egész mátrixokból bonyolult algebrai számok keletkezzenek.

A 14.3-as verzióban emellett hozzáadunk néhány egyszerű mátrixgenerátort is, amelyek kényelmesen használhatók olyan függvényekkel együtt, mint a FrobeniusDecomposition:

 

 

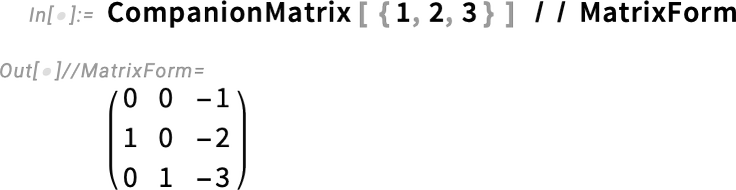
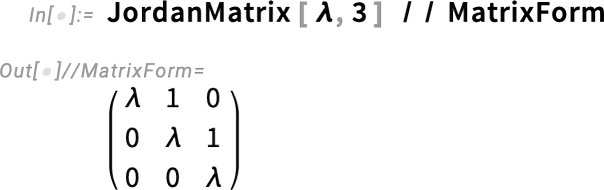
Az új függvények egy másik csoportja lényegében a mátrixokat és az (egy­változós) polinomokat kapcsolja össze. Már hosszú ideje rendelkezünk a következőkkel:

 

Most pedig hozzáadjuk a MatrixMinimalPolynomial függvényt:

 

Hozzáadjuk továbbá a MatrixPolynomialValue függvényt is — ez a MatrixFunction egyfajta polinomiális speciális esete, amely kiszámítja egy polinom (mátrix)értékét, amikor a változó (például m) mátrixértéket vesz fel.

 

És igen, ez megmutatja, hogy — ahogyan a Cayley–Hamilton-tétel kimondja — a mátrix kielégíti a saját karakterisztikus egyenletét.

A 6.0-s verzióban vezettük be a HermiteDecomposition függvényt egész mátrixokra. Most pedig, a 14.3-as verzióban, hozzáadunk egy változatot polinommátrixokra is — amely az eliminációs folyamat során a GCD helyett a PolynomialGCD függvényt használja.

 

Előfordul azonban, hogy nem szeretnél teljes felbontásokat kiszámítani, hanem csak a redukált alakra van szükséged. Ezért a 14.3-as verzióban hozzáadjuk az önálló redukciós függvényeket: HermiteReduce és PolynomialHermiteReduce (valamint a SmithReduce-ot):

 

Még egy újdonság a mátrixok terén a 14.3-as verzióban: néhány kiegészítő jelölés, amely különösen kényelmes szimbolikus mátrixkifejezések írásához. Példa erre a Norm új, StandardForm változata:

 

Ezt korábban már használtuk a TraditionalForm-ban; most már a StandardForm-ban is elérhető. A beírásához egyszerűen töltsd ki a ESC norm ESC-gel előhívott sablont. Néhány más jelölés, amelyet hozzáadtunk:

 

 

 

 

With[ ] Goes Multi-argument

Az elmúlt 37 év minden egyes verziójában folyamatosan finomítottuk a Wolfram Language kialakításának részleteit (miközben mindvégig megőriztük a kompatibilitást). A 14.3-as verzió sem kivétel.

Van azonban valami, amire sok-sok éve vágytam — technikailag nehéz volt megvalósítani, és csak most vált lehetővé: a többargumentumos With.

Gyakran előfordul, hogy With szerkezeteket egymásba ágyazok:

 

De miért ne lehetne ezt egyszerűen egyetlen, többargumentumos With-sé lapítani? Nos, a 14.3-as verzióban ez most már lehetséges:

 

A beágyazott With-hez hasonlóan ez először az x-et helyettesíti 1-gyel, majd az y-t x + 1-gyel. Ha azonban mindkét helyettesítés „párhuzamosan” történik, akkor y az eredeti, szimbolikus x-et kapja meg, nem pedig a már behelyettesített értéket.

 

Honnan lehetett volna megkülönböztetni a kettőt? Figyeld meg alaposan a szintaxiskiemelést. A többargumentumos esetben az x az y = x + 1 kifejezésben zöld, ami azt jelzi, hogy lokális (scoped) változó; a nem többargumentumos esetben viszont kék, ami azt jelzi, hogy globális változó.

Mint kiderült, a szintaxiskiemelés az egyik legtrükkösebb kérdés a többargumentumos With megvalósításában. Észre fogod venni, hogy ahogy további argumentumokat adsz hozzá, a változók megfelelően zöldre váltanak, jelezve, hogy lokális hatókörbe tartoznak. Emellett, ha ütközések vannak a változók között, azok pirosra váltanak.

 

 

 

 

 

Ciklikus[ ] és ciklikus listák

Mi az 5. eleme egy 3 elemű listának? Mondhatnánk egyszerűen, hogy ez hiba. Egy másik lehetőség viszont az, hogy a listát ciklikusnak tekintjük. És pontosan ezt teszi az új Cyclic függvény a 14.3-as verzióban:

 

A Cyclic[{a, b, c}] úgy is felfogható, mint a {a, b, c} végtelen ismétléséből álló sorozat. Ez egyszerűen a {a, b, c} első részét adja vissza:

 

De ez „körbefordul”, és a {a, b, c} utolsó részét adja vissza:

 

Bármely „ciklikus elemet” kiválaszthatod; valójában mindig csak az általad megadott elemtömb hosszával vett maradék (modulo) szerinti elemet választod ki.

 

A Cyclic lehetőséget ad arra, hogy gyakorlatilag végtelen, ismétlődő listákkal végezzünk számításokat. Ugyanakkor kevésbé „számítási” jellegű helyzetekben is hasznos — például ciklikus stílusok megadására, mondjuk egy Grid esetében.

 

 

 

 

 

Új a Tabularban

A 14.2-es verzió áttörést jelentő képességeket vezetett be a gigabájt méretű táblázatos adatok kezelésében, a vadonatúj Tabular függvényre építve. A 14.3-as verzióban tovább bővítjük a Tabular lehetőségeit több területen.

Az első bővítés arra vonatkozik, hogy honnan lehet adatokat importálni a Tabular számára. A helyi fájlok és URL-ek mellett a 14.2-es verzió már támogatta az Amazon S3, az Azure blob storage, a Dropbox és az IPFS használatát. A 14.3-as verzióban ehhez hozzáadjuk a OneDrive-ot és a Kaggle-t is. Emellett bevezetjük annak lehetőségét is, hogy relációs adatbázisokból „nagy kortyokban” töltsük be az adatokat. Már a 14.2-es verzióban is lehetővé tettük, hogy a Tabular segítségével rendkívül hatékony módon, „out-of-core” feldolgozással kezeljük a relációs adatbázisokban tárolt adatokat. A 14.3-as verzióban pedig már közvetlenül is importálhatók a lekérdezések eredményei memórián belüli (in-core) feldolgozásra olyan relációs adatbázisokból, mint az SQLite, a Postgres, a MySQL, az SQL Server és az Oracle. Mindez a DataConnectionObject segítségével működik, amely egy aktív adatkapcsolat szimbolikus reprezentációját adja, és kezeli többek között az olyan kérdéseket is, mint a hitelesítés.

Íme egy példa egy adatkapcsolat-objektumra, amely egy mintadatbázison végrehajtott adott lekérdezés eredményeit reprezentálja:

 

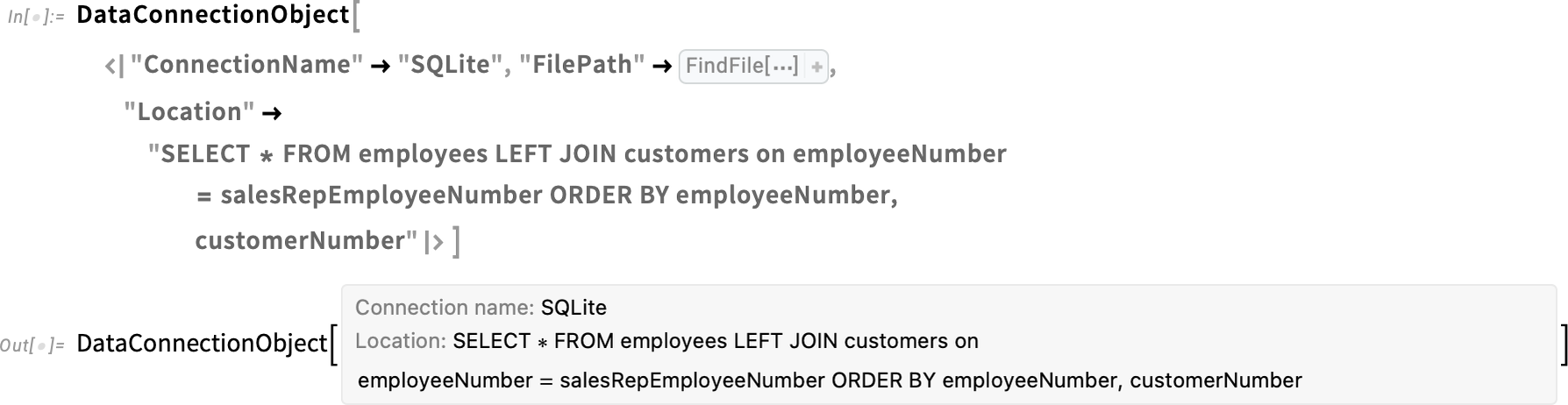
Az Import ezt fel tudja dolgozni, és egy (memórián belüli, in-core) Tabular objektummá alakítani:

 

A nagy mennyiségű táblázatos adat egyik gyakori forrása a naplófájlok. A 14.3-as verzióban rendkívül hatékony módon tesszük lehetővé az Apache naplófájlok importálását Tabular objektumokba. Emellett új importálási lehetőségeket adunk hozzá a Common Log és az Extended Log fájlokhoz, valamint a JSON Lines fájlok importálásához (és exportálásához) is:

 

Ezenfelül több más formátum esetében is lehetővé tesszük az adatok Tabular objektumként történő importálását (MDB, DBF, NDK, TLE, MTP, GPX, BDF, EDF). A 14.3-as verzió egy további újdonsága (például GPX adatoknál használva) a „GeoPosition” oszloptípus.

Amellett, hogy új módokat kínálunk az adatok Tabular objektumokba történő betöltésére, a 14.3-as verzió kibővíti a táblázatos adatok kezelésének lehetőségeit is, különösen több Tabular objektumból származó adatok egyesítését. Az egyik új, ezt szolgáló függvény a ColumnwiseCombine. A ColumnwiseCombine alapötlete az, hogy több Tabular objektumot vesz, megvizsgálja az ezekben szereplő sorok összes lehetséges kombinációját, majd egyetlen új Tabular objektumot hoz létre, amely csak azokat az egyesített sorokat tartalmazza, amelyek megfelelnek egy megadott feltételnek.

Tekintsük az alábbi három Tabular objektumot:

 

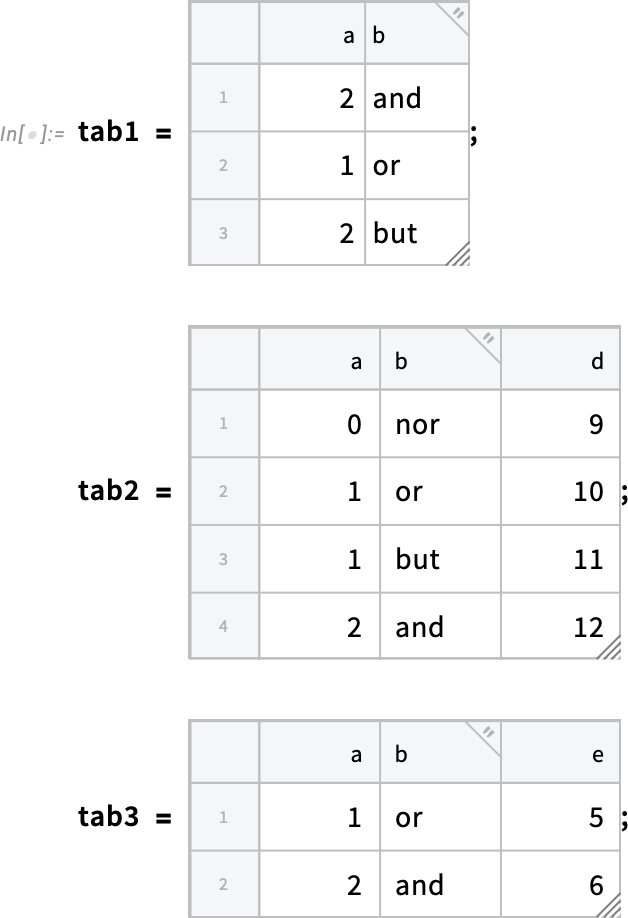
Íme egy példa a ColumnwiseCombine használatára, ahol az egyesített sor bekerülésének feltétele az, hogy az „a” és „b” oszlopok értékei megegyezzenek az éppen egyesített sor különböző példányaiban:

 

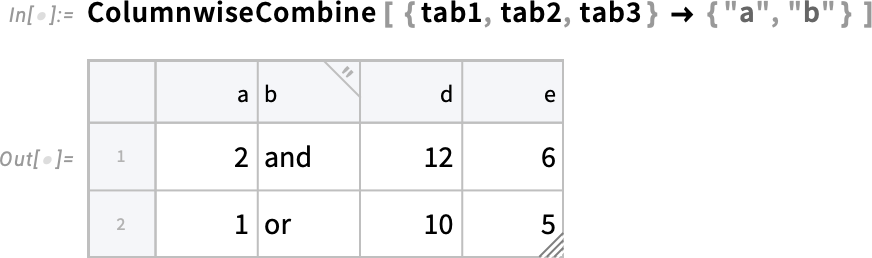
Számos finom részletkérdés merülhet fel. Itt egy „outer” kombinációt hajtunk végre, amelyben gyakorlatilag azt feltételezzük, hogy egy sorból hiányzó elem is megfelel a kritériumnak (és ennek megfelelően azokat a sorokat is bevesszük, amelyekhez ezek az explicit „hiányzó elemek” hozzá vannak adva):

 

Íme egy további finom részlet. Ha különböző Tabular objektumokban azonos nevű oszlopok szerepelnek, hogyan lehet megkülönböztetni az ezekből származó elemeket? Itt gyakorlatilag minden Tabular objektumnak adunk egy nevet, amelyet aztán a keletkező, egyesített Tabular objektumban egy kibővített kulcs kialakításához használunk:

 

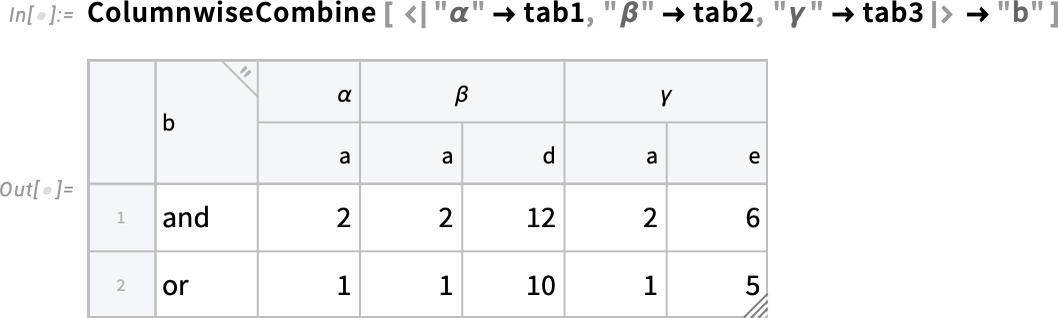
A ColumnwiseCombine lényegében a JoinAcross n-áris általánosítása (amely gyakorlatilag a relációs algebra „join” műveletét valósítja meg). A 14.3-as verzióban a JoinAcross függvényt is továbbfejlesztettük, hogy a Tabular további funkcióit is kezelje, például a kibővített kulcsok megadását. Mind a ColumnwiseCombine, mind a JoinAcross esetében úgy alakítottuk ki a működést, hogy tetszőleges függvényt lehessen használni annak eldöntésére, hogy a sorokat össze kell-e kapcsolni.

Miért érdemes olyan függvényeket használni, mint a ColumnwiseCombine és a JoinAcross? Tipikus eset, amikor több Tabular objektum áll rendelkezésre, amelyek egymást metsző adathalmazokat tartalmaznak, és ezeket szeretnénk „összeszőni” az egyszerűbb feldolgozás érdekében. Például tegyük fel, hogy van egy Tabular objektumunk, amely az izotópok tulajdonságait tartalmazza, és egy másik, amely az elemek tulajdonságait — és most egy egyesített táblát szeretnénk létrehozni az izotópokról, immár az elemek táblájából átvett további oszlopokkal kiegészítve:

 

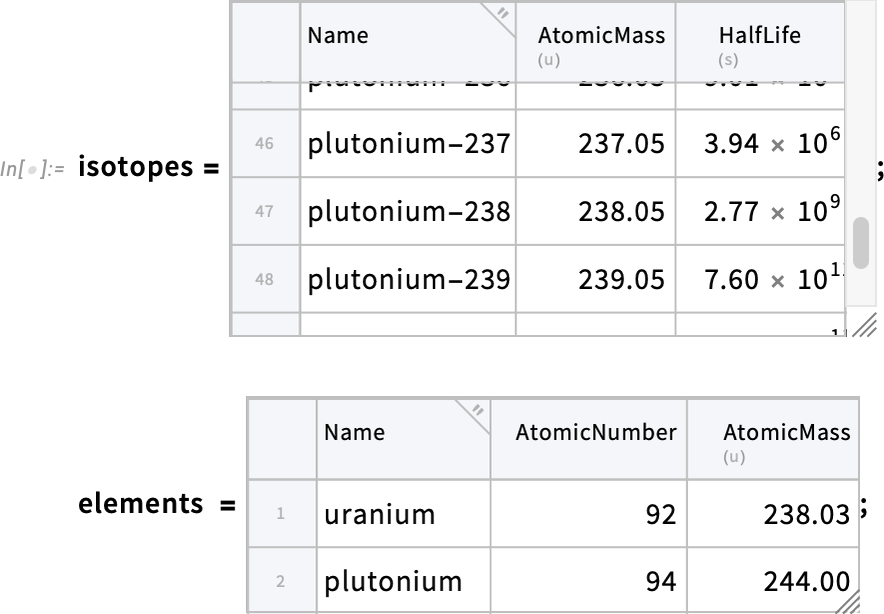
Az egyesített Tabular objektumot a JoinAcross segítségével hozhatjuk létre. Ebben a konkrét esetben azonban — ahogyan az a valós adatoknál gyakran előfordul — az adattáblák „összeszövése” kissé körülményes. Úgy oldjuk meg, hogy a JoinAcross harmadik („összehasonlító függvény”) argumentumát használjuk, és azt adjuk meg, hogy a sorok akkor legyenek összekapcsolva, ha az izotópok táblájában a „Name” oszlop bejegyzésének megfelelő karakterlánc eleje megegyezik az elemek táblájában a „Name” oszlophoz tartozó karakterlánc elejével:

 

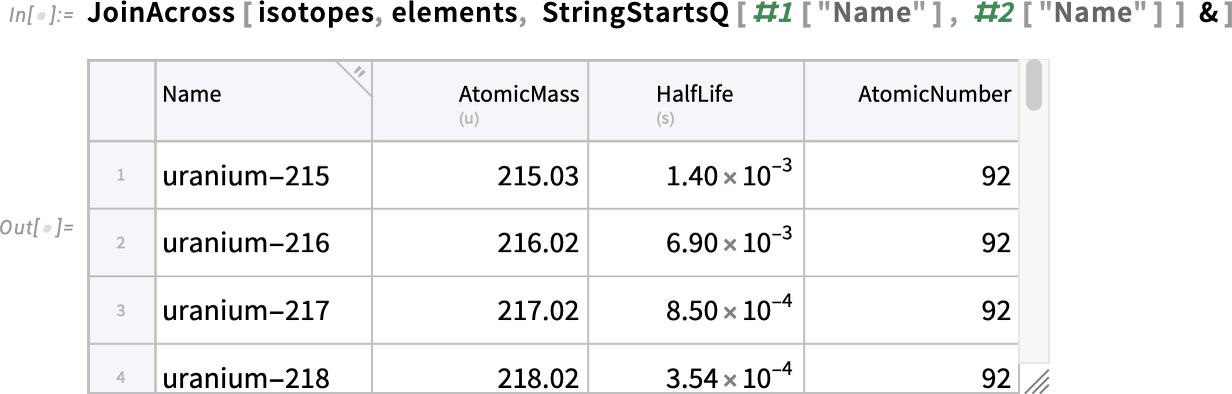
Alapértelmezés szerint az eredményben egy adott névvel csak egy oszlop jelenik meg. Tehát itt a „Name” oszlop az első Tabular objektumból származik a JoinAcross-ban (vagyis az izotópok táblából); az „AtomicNumber” oszlop például a másodikból (vagyis az elemek táblából). Az oszlopokat a „forrásuk” szerint megkülönböztethetjük úgy, hogy kulcsot adunk meg a JoinAcross-ban:

 

Most tehát rendelkezünk egy egyesített Tabular objektummal, amely „összeszőtte” az adatokat mindkét eredeti Tabular objektumból — ez a JoinAcross tipikus alkalmazása.

 

 

 

Táblázatos formázás

A Tabular segítségével rengeteg hatékony feldolgozás végezhető. Ugyanakkor a Tabular az adatok tárolására és megjelenítésére is szolgál. A 14.3-as verzióban elkezdtük bevezetni azokat a lehetőségeket, amelyekkel formázhatók a Tabular objektumok és azok tartalma. Vannak egyszerűbb dolgok is: például most már a ImageSize segítségével programozottan beállítható a Tabular kezdeti megjelenítési mérete (a méretet természetesen mindig interaktívan is módosíthatjuk a jobb alsó sarokban található átméretező fogantyúval):

 

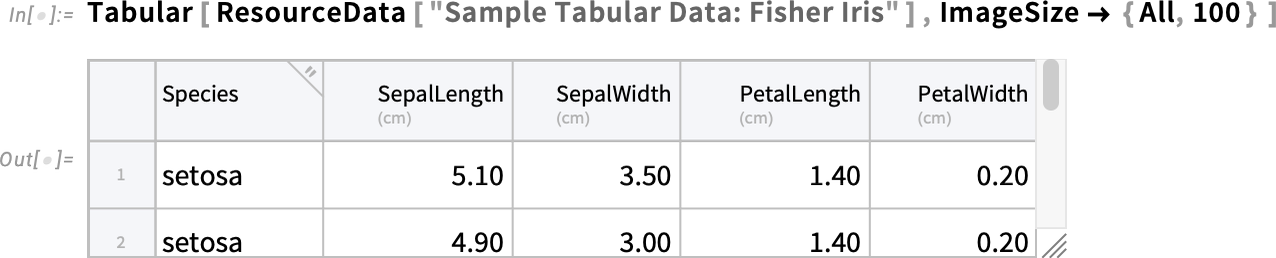
A AppearanceElements segítségével azt is szabályozhatjuk, hogy mely vizuális elemek jelenjenek meg. Itt például azt kérjük, hogy az oszlopfejlécek legyenek láthatók, de a sorcímkék és az átméretező fogantyú ne jelenjenek meg:

 

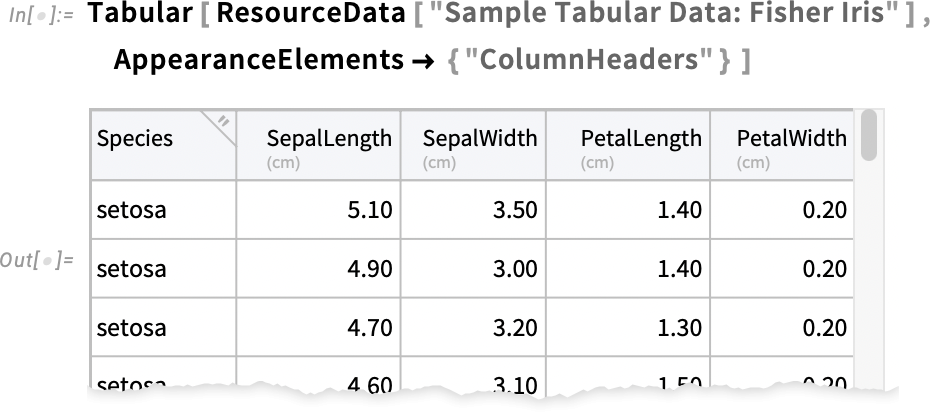
Rendben, de mi a helyzet az adattartomány formázásával? A 14.3-as verzióban például a Background opcióval megadható a háttér. Itt azt kérjük, hogy a sorok váltakozva legyenek háttér nélkül vagy világos zölddel (pont, mint a régi line printer papírokon!):

 

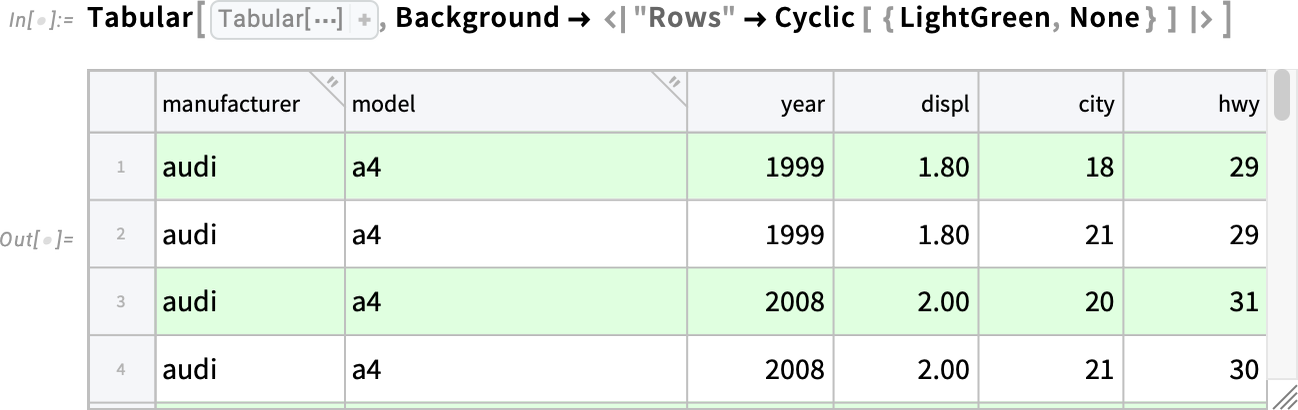
Ez a beállítás a háttérszínt mind a sorokra, mind az oszlopokra alkalmazza, és ahol átfedik egymást, ott a színek megfelelően keverednek:

 

Ez a beállítás csak egyetlen oszlopot emel ki, azáltal, hogy háttérszínt adunk neki, és az oszlopot a neve alapján jelöljük ki:

 

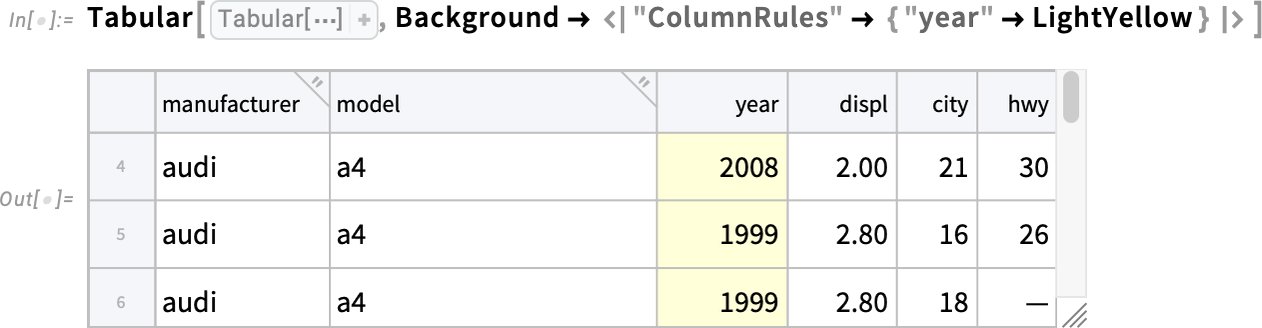
A Background mellett a 14.3-as verzióban már a Tabular tartalmának formázására is használható az ItemStyle. Itt például azt adjuk meg, hogy a „year” oszlop legyen félkövér és piros:

 

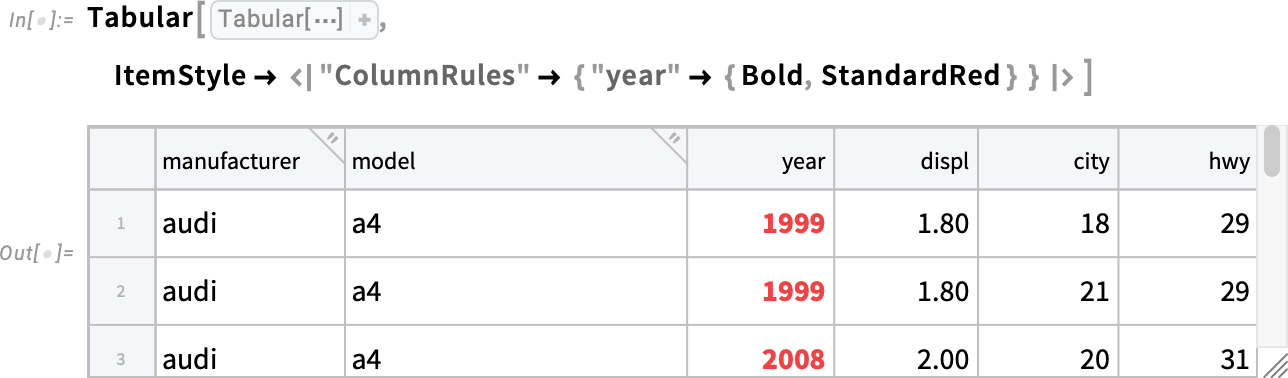
De mi történik, ha azt szeretnénk, hogy a Tabular elemeinek formázása ne a pozíciójuk, hanem az értékük alapján történjen? A 14.3-as verzió erre is lehetőséget ad kulcsok segítségével. Például itt minden olyan sorhoz háttérszínt adunk, ahol a „hwy” értéke 30 alatti:

 

Ugyanezt megtehetjük úgy is, hogy a színt valójában a „hwy” értékéből számítjuk ki (vagyis az értékből, amelyet az oszlop teljes minimum–maximum tartománya alapján átskálázunk):

 

Az utolsó sor itt nincs színezve — mert a „hwy” oszlopban az érték hiányzik. Ha pedig például az összes hiányzó értéket szeretnénk kiemelni, egyszerűen így tehetjük meg:

 

 

 

 

 

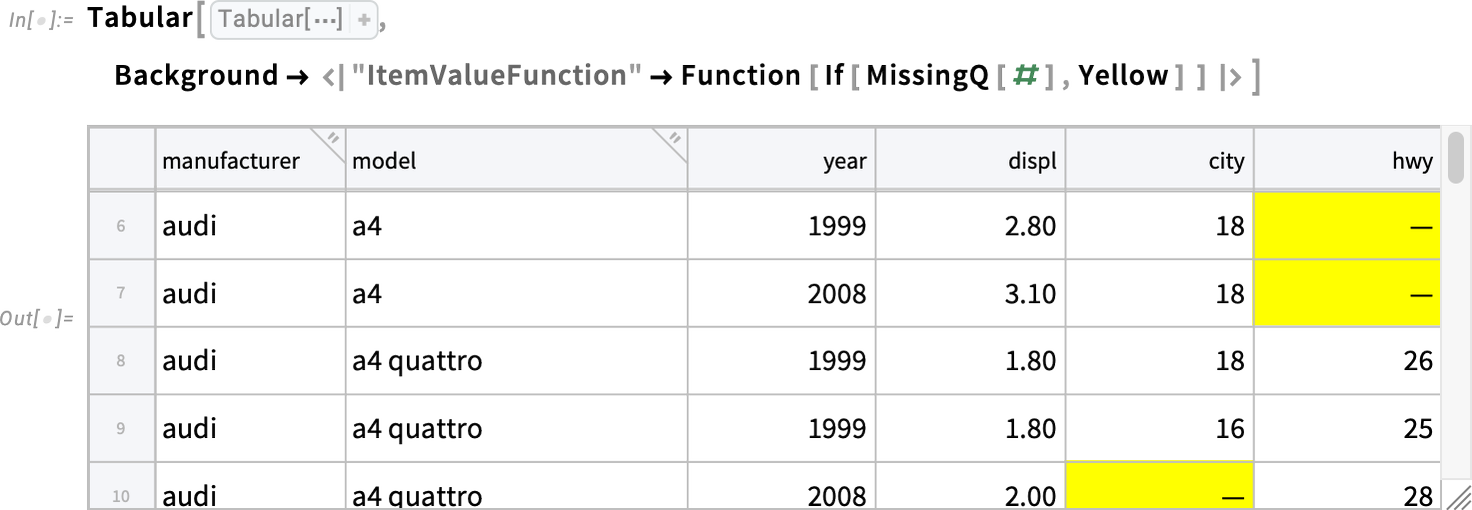
Szemantikus rangsorolás, szöveges jellemzők kinyerése és minden, ami ehhez kapcsolódik

Melyik választásra gondolsz? Tegyük fel, hogy van egy listád — például egy éttermi menü. És leírod szövegesen, hogy mit szeretnél ezek közül. Az új SemanticRanking függvény a leírásod alapján rangsorolja a lehetőségeket:

 

És mivel ez modern nyelvi modell módszereket használ, a választások például nemcsak angolul, hanem bármely nyelven megadhatók.

Ha szeretnéd, a SemanticRanking arra is képes, hogy például relevancia pontszámokat adjon:

 

Hogyan kapcsolódik a SemanticRanking a 14.1-es verzióban bevezetett SemanticSearch funkcióhoz? A SemanticSearch valójában alapértelmezés szerint a SemanticRanking-et használja a találatok végső rangsorolására. A SemanticSearch azonban — ahogy a neve is sugallja — egy potenciálisan nagy anyagmennyiségben keres, és adja vissza a legrelevánsabb elemeket. Ezzel szemben a SemanticRanking egy kisebb „menü” lehetőségeit veszi, és mindegyiket rangsorolja a relevancia alapján, amit megadsz.

A SemanticRanking lényegében a SemanticSearch feldolgozási láncának egyik elemét teszi közvetlenül elérhetővé. A 14.3-as verzióban egy másik elemet is hozzáférhetővé teszünk: egy továbbfejlesztett FeatureExtract változatot szövegre, amely előre betanított, és nem igényel saját, explicit példákat:

 

Az új szöveges feature extractor továbbfejleszti a Classify, Predict, FeatureSpacePlot és hasonló funkciókat mondatok vagy más szöveges tartalmak esetén is.

 

 

 

 

Lefordított függvények, amelyek képesek szüneteltetni és folytatni a folyamatot

A Wolfram Language tipikus számítási folyamata úgy működik, hogy egymás után hívunk függvényeket: minden függvény lefut, visszaadja az eredményét, majd a következő függvény fut le. A 14.3-as verzió azonban — a Wolfram Language fordító kontextusában — lehetővé tesz egy másikfajta folyamatot, amelyben a függvények bármikor szüneteltethetők, majd később folytathatók. Gyakorlatilag egy coroutine-szerű működést valósítottunk meg, amely lehetővé teszi a lépcsőzetes számítást, és például támogatja a „generátorokat”, amelyek egymás után adnak eredményeket, mindig megőrizve a további számításhoz szükséges állapotot.

Az alapötlet, hogy létrehozzunk egy IncrementalFunction objektumot, amely lefordítható. Az IncrementalFunction az IncrementalYield segítségével ad vissza „lépcsőzetes” eredményeket, és tartalmazhat IncrementalReceive függvényeket is, amelyek lehetővé teszik, hogy a futás közben további bemenetet kapjon.

Íme egy nagyon egyszerű példa, amely egy lépcsőzetes függvényt hoz létre (egy „IncrementalFunction” típusú DataStructure-ként reprezentálva), amely sorban generálja a 2 hatványait:

 

Mostantól minden alkalommal, amikor a „Next” elemet kérjük ettől, a lépcsőzetes függvényünk kódja lefut, amíg el nem éri az IncrementalYield-t, ekkor pedig visszaadja a megadott eredményt:

 

 

 

Gyakorlatilag a lefordított lépcsőzetes függvény mindig belsőleg megőrzi az állapotot, így amikor a „Next” elemet kérjük, egyszerűen onnan folytatja a futást, ahol abbahagyta.

Íme egy kicsit bonyolultabb példa: a Fibonacci-rekurzió lépcsőzetes (incremental) változata:

 

Minden alkalommal, amikor a „Next” elemet kérjük, megkapjuk a következő értéket a Fibonacci-sorozatban:

 

 

A lépcsőzetes függvény úgy van beállítva, hogy a „Next” elem kérésekor az a értékét adja vissza, miközben belsőleg mind a, mind b értékét megőrzi, így készen áll arra, hogy a következő „Next” elem kérésekor folytassa a futást.

Általánosságban az IncrementalFunction egy új és gyakran kényelmes módot kínál a kód megszervezésére. Lehetővé teszi, hogy ismételten futtass egy kódrészletet és kapj eredményeket, miközben a fordító automatikusan megőrzi az állapotot, így neked nem kell explicit módon gondoskodnod erről, vagy külön kódot írnod hozzá.

Egy gyakori felhasználási eset az enumeráció. Tegyük fel, hogy van egy algoritmusod bizonyos típusú objektumok felsorolására. Az algoritmus felépít egy belső állapotot, amely lehetővé teszi új objektumok generálását. Az IncrementalFunction segítségével lefuttathatod az algoritmust addig, amíg generál egy objektumot, majd megállíthatod, miközben az állapot automatikusan megmarad, hogy újra folytathasd.

Például itt egy lépcsőzetes függvény, amely egy adott lista összes lehetséges párosítását generálja:

 

Mondjuk neki, hogy egy egymillió elemű lista összes lehetséges párját generálja:

 

Az összes lehetséges pár teljes gyűjteménye nem férne el a számítógép memóriájában. Azonban a lépcsőzetes függvénnyel egymás után kérhetünk egyes párokat, miközben a függvény belső állapota megőrzi, hogy éppen hol tartunk a generálásban:

 

 

 

Egy másik példa az IncrementalFunction használatára, amikor fokozatosan fogyasztunk valamilyen külső adatfolyamot, például egy fájlból vagy API-ból érkező adatot.

Az IncrementalFunction a Wolfram Language új, alapvető képessége, amelyet a jövőbeni verziókban arra fogunk használni, hogy számos új „lépcsőzetes” (incremental) funkciót építsünk, amelyek lehetővé teszik, hogy kényelmesen dolgozzunk olyan objektumgyűjteményekkel, amelyeket egyszerre nem lehetne teljesen generálni vagy kezelni.

 

 

 

 

Gyorsabb, simább, beágyazott külső számítástechnika

Évtizedeken át keményen dolgoztunk azon, hogy a Wolfram Language-en belül a munkafolyamatok a lehető legzökkenőmentesebbek legyenek. De mi a helyzet, ha külső kódot szeretnél meghívni? Nos, ott kint igazi dzsungel van, tele kompatibilitási problémákkal, függőségekkel stb. Évek óta folyamatosan azon dolgozunk, hogy a Wolfram Language-en belül a lehető legjobb interfészt biztosítsuk a külső kódhoz. Valójában, amit sikerült biztosítanunk, sok esetben sokkal gördülékenyebb élményt nyújt, mint a hagyományosan használt natív eszközök.

A 14.3-as verzió számos előrelépést tartalmaz a külső kód kezelésében. Először is, Python esetében drasztikusan felgyorsítottuk a Python futtatókörnyezetek előkészítését. Még a Python első használatakor is most már csak néhány másodpercbe telik, hogy a környezet létrejöjjön. A 14.2-es verzióban vezettünk be egy nagyon letisztult módot a függőségek megadására. A 14.3-as verzióban pedig a futtatókörnyezetek adott függőségekkel történő előkészítése is nagyon gyors lett:

 

És igen, egy ilyen függőségekkel rendelkező Python futtatókörnyezet most már a gépeden kerül előre beállításra, így ha legközelebb meghívod, azonnal futtatható, további előkészítés nélkül.

A 14.3-as verzió másik nagy előrelépése a rendkívül egyszerűsített mód az R nyelv használatára a Wolfram Language-en belül. Csak add meg az R-t külső nyelvként, és automatikusan telepítésre kerül a rendszereden, majd lefuttatható egy számítás (igen, a „rnorm” funkciónév, amely a Gauss-eloszlású véletlenszámok generálására szolgál, kicsit bántja a nyelvtervezési érzékemet, de…):

 

Az R-t közvetlenül jegyzetfüzetben is használhatod (írd be a > jelet egy External Language cella létrehozásához):

 

Az egyik technikai kihívás az volt, hogy lehetővé tegyük az R kód futtatását különböző függőségekkel egyetlen Wolfram Language munkameneten belül. Ezt korábban nem tudtuk megoldani (és bizonyos szempontból az R alapból nem is erre van tervezve). A 14.3-as verzióban azonban úgy állítottuk be a rendszert, hogy több R munkamenet is futhat a Wolfram Language munkameneteden belül, mindegyik saját függőségekkel és saját előkészítéssel. (Ez rendkívül bonyolult, és bizonyos kóros esetekben az R világa annyira összetett lehet, hogy nem lehetséges a működés, de az ilyen esetek legalábbis nagyon ritkák.)

A 14.3-as verzió másik újdonsága az R-rel kapcsolatban az ExternalFunction támogatása, így az R-ben írt kódot ugyanúgy használhatod, mint bármely más függvényt a Wolfram Language-ben.

 

 

 

 

Jegyzetfüzetekből prezentációk: A képarány kihívásának megoldása

A jegyzetfüzetek általában görgethető dokumentumoknak vannak szánva. De — különösen, ha előadást készítesz — néha inkább diavetítés-szerű formát szeretnél („PowerPoint-stílusban”). Korábban már több megközelítés létezett, de a 14.3-as verzió elődjében, a 11.3-ban — hét évvel ezelőtt — vezettük be a Presenter Tools-t, mint egyszerű módot arra, hogy jegyzetfüzeteket alakíts előadásokhoz.

A működés nagyon kényelmes. Kezdhetsz teljesen új jegyzetfüzettel, vagy átalakíthatsz egy meglévőt. A végeredmény egy diavetítés-szerű prezentáció, amelyet például prezentációs távirányítóval is léptethetsz. Természetesen mivel ez egy jegyzetfüzet, rengeteg további kényelmi funkciót is kapsz: például Manipulate-et használhatsz a „diádon”, cellacsoportokat nyithatsz és zárhatsz, szerkesztheted a „diát”, végezhetsz számításokat stb. Mindez nagyon gördülékenyen működik.

Volt azonban mindig egy nagy probléma: milyen képarányúak legyenek a diák? A cél az, hogy teljes képernyőn, akár kivetítve jelenjenek meg, de hogyan illeszkedik ez a tartalomhoz? Szöveg esetében mindig lehet újraformázni a sorokat a másik képarányhoz. A grafika és képek esetében azonban nehezebb, mert ezek már rendelkeznek saját képaránnyal. Különösen, ha szokatlan formátumúak (pl. magas és keskeny), könnyen előfordulhat, hogy a diák görgetést igényelnek, vagy nem néznek ki jól, nem kényelmesek.

A 14.3-as verzióban azonban van egy zökkenőmentes megoldás erre, amit én személy szerint nagyon hasznosnak találok.

Válaszd a File > New > Presenter Notebook… menüpontot, majd nyomd meg a Create gombot egy új, üres presenter jegyzetfüzet létrehozásához:

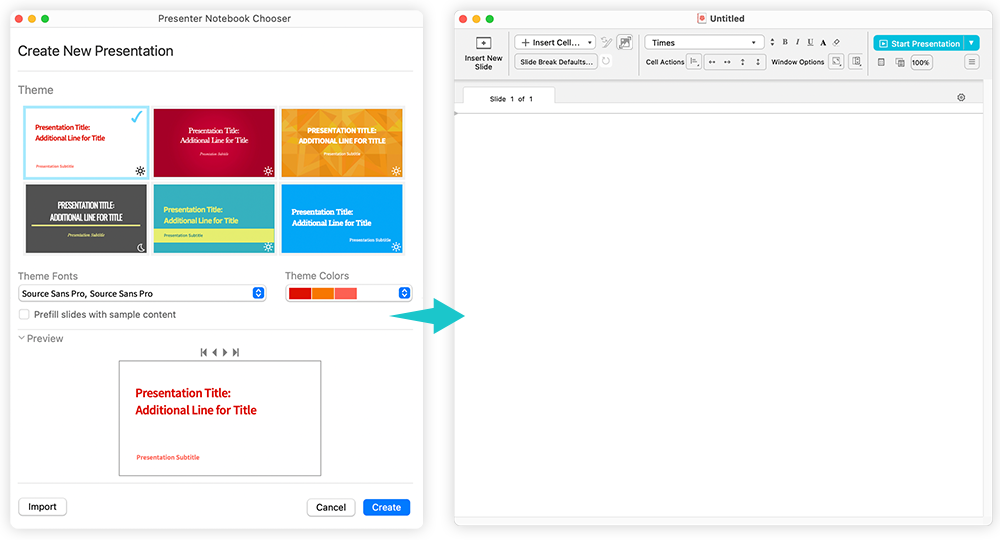
A eszköztáron most már van egy új gomb, amely egy teljes diás kép- vagy grafika sablont szúr be:

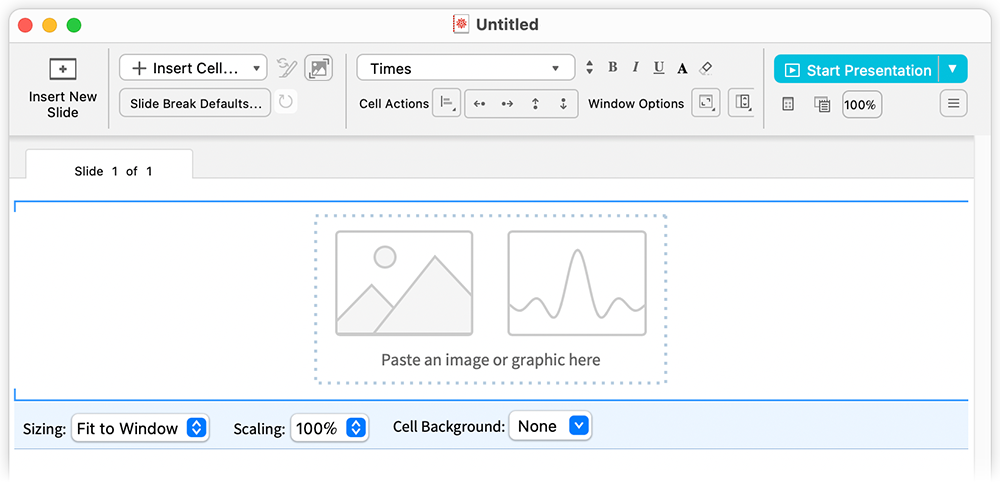
Ezután a kép automatikusan kitölti a teljes diát, miközben megtartja a saját képarányát, így nem kell görgetned, és a diák mindig jól néznek ki:

Nyomd meg a gombot, és teljes képernyős prezentációt kapsz — minden elem megfelelően méretezve: a rövid és széles grafika a képernyő szélességét tölti ki, míg a magas és keskeny grafika a képernyő magasságát foglalja el:

Amikor egy teljes diás képet szúrsz be, mindig megjelenik egy „vezérlősáv” a kép alatt:

Az első legördülő menü

Az első legördülő menüvel eldöntheted, hogy a kép illeszkedjen a képernyőhöz, vagy inkább horizontálisan töltse ki a képernyőt, esetleg a tetején és alján levágódjon.

Ne feledd, hogy ez a sablon teljes diás képek elhelyezésére szolgál. Ha például helyet szeretnél hagyni feliratnak, a dia többi részén, akkor 100%-nál kisebb méretet kell választanod.

Alapértelmezés szerint a létrehozott cellák háttérszíne a választott presenter notebook témától függ. A példában a háttér alapértelmezettként fehér lesz. Ez azt jelenti, hogy ha például kivetíted a képeket, mindig lesz egy fehér téglalap a háttérben. Ha azonban azt szeretnéd, hogy a kép természetes képarányában jelenjen meg, környezet nélkül, válaszd a Cell Background opciót, és állítsd feketére.

 

 

 

 

Még több felhasználói felület csiszolás

Már 38 éve, hogy feltaláltuk a jegyzetfüzeteket… mégis minden új verzióban tovább csiszoljuk és fejlesztjük a működésüket. Íme egy példa erre. Közel 30 évvel ezelőtt vezettük be azt az ötletet, hogy ha begépeled a -> karaktereket, azok automatikusan a sokkal elegánsabb jellé alakulnak. Négy évvel ezelőtt (a 12.3-as verzióban) finomítottunk ezen az elképzelésen: a -> valójában nem lett lecserélve →-re, hanem csak így jelent meg vizuálisan. De itt felmerül egy apró, mégis fontos kérdés: ha a kurzorral visszafelé lépsz a → jelben, akkor vajon láthatók-e azok a karakterek, amelyekből felépül? A korábbi verziókban igen — a 14.3-as verzióban viszont már nem. Ez egy tapasztalatból fakadó döntés: ha valami egyetlen karakternek látszik (itt a →), akkor furcsa és zavaró, ha kurzormozgás közben „szétesik”. Ezért most már nem történik meg. Ugyanakkor, ha Backspace-t használsz (nem pedig nyílbillentyűt), akkor a jel szétesik, így továbbra is szerkeszthetők az egyes karakterek. Igen, ez egy finom részlet — de pontosan az ilyen apróságok teszik a Wolfram Notebook élményt ennyire gördülékennyé. Íme egy másik fontos kis kényelmi funkció, amelyet a 14.3-as verzióban vezettünk be: az egyetlen karakteres elhatárolók automatikus körbefogása. Tegyük fel, hogy ezt gépeled be:

Nagy valószínűséggel valójában egy listát szerettél volna. Ezt meg is kaphatod, ha a { jelet az elejére, a } jelet pedig a végére teszed. Most azonban van egy sokkal egyszerűbb megoldás. Egyszerűen jelöld ki az egészet…

…és most egyszerűen gépeld be a { jelet. A { … } automatikusan köré kerül a kijelölésnek.

Ugyanez működik a ( … ), [ … ] és a „ … ” esetében is.

Elsőre talán apróságnak tűnik. De ha sok kód van a képernyőn, rendkívül kényelmes, hogy nem kell ide-oda lépkedni az elhatárolók hozzáadásához — elég kijelölni egy rész-kifejezést, majd begépelni egyetlen karaktert.

Számos változtatást vezettünk be az ikonokban, súgókban (tooltipekben) stb., egyszerűen azért, hogy minden átláthatóbb legyen. Egy másik újdonság az is, hogy végre támogatott a brit és az amerikai angol helyesírási szótár külön kezelése. Alapértelmezés szerint a rendszer automatikusan az operációs rendszered beállításai alapján választja ki, melyiket használja. Így a „color” vs. „colour” és a „center” vs. „centre” most már a beállított preferenciáidat követi, és ennek megfelelően kerül megjelölésre. Egyébként, ha esetleg kíváncsi lennél: évek óta saját helyesírási szótárakat gondozunk. Sőt, rendszeresen küldök be új szavakat hozzáadásra — vagy azért, mert gyakran használom őket, vagy igen, azért is, mert egyszerűen kitaláltam őket (például: „ruliad”, „emes”, stb.).

 

 

 

Árleszállítás!

Olyan fájlt szeretnél, amely egyszerű szöveg (plaintext), mégis formázott. Manapság ennek egyik legelterjedtebb módja a Markdown használata. Ez egy olyan formátum, amelyet emberek és MI-k egyaránt könnyen olvasnak, és amely vizuálisan is „felöltöztethető” formázással. Nos, a 14.3-as verzióban a Markdown könnyen elérhető formátummá válik a Wolfram Notebookokban, és általában a Wolfram Language-ben is.

Érdemes rögtön az elején leszögezni, hogy a Markdown messze nem olyan gazdag, mint a szabványos Notebook formátumunk. Ennek ellenére a notebookok számos kulcsfontosságú eleme jól megragadható Markdownban. (Egyébként a .nb notebook fájlok — akárcsak a Markdown — szintén tiszta szövegfájlok, de mivel a notebook tartalom minden aspektusát hűen kell reprezentálniuk, elkerülhetetlenül nem olyan tömörek és könnyen olvashatók, mint a Markdown fájlok.)

Rendben, tegyük fel, hogy van egy Notebookod:

A Markdown verziót a Fájl > Mentés másként > Markdown paranccsal töltheted le:

Így néz ki ez egy Markdown-nézőben:

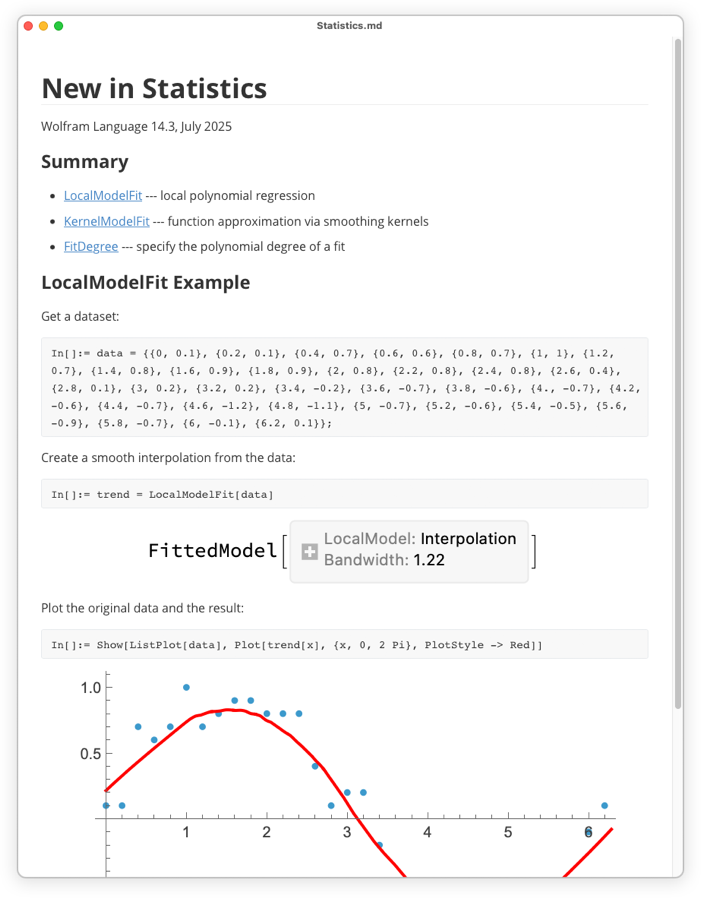
A notebook főbb jellemzői megjelennek benne, de bizonyos részletek hiányoznak (például a cellák háttérszínei, a valódi matematikai szedés stb.), és a megjelenítés határozottan nem olyan szép, mint a rendszerünkben, illetve nem is olyan funkcionális (például nincsenek bezárható cellacsoportok, nincs dinamikus interaktivitás stb.).

Rendben, tegyük fel, hogy van egy Markdown fájlod. A 14.3-as verzióban most már egyszerűen használhatod a File > Open menüpontot, kiválaszthatod a „Markdown Files” fájltípust, és megnyithatod a Markdown fájlt Notebookként.

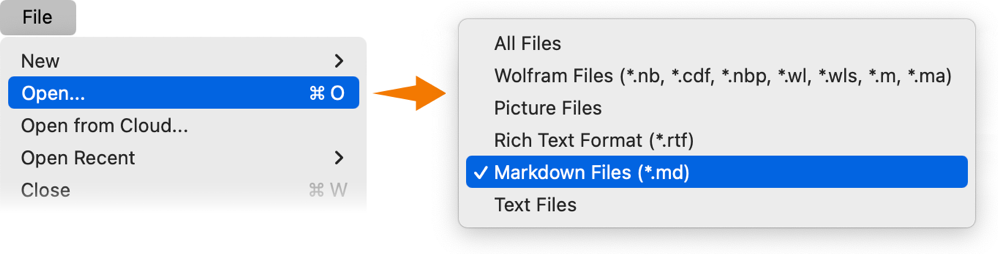
A Markdownon keresztüli oda-vissza konvertálás során a Notebook néhány finom részlete elveszik, de az alapvető szerkezet megmarad. És igen, így a „vadonból származó” Markdown fájlokat is megnyithatod — például jegyzetalkalmazásokból, szoftverdokumentációkból, nyers LLM-kimenetekből stb.

A Markdown kezelését nemcsak teljes fájl szinten támogatjuk, hanem Markdown-részletek létrehozását (és beolvasását) is. Így például egy Notebookban lévő táblát egyszerűen kijelölhetsz, majd a Copy As > Markdown paranccsal megkaphatod annak Markdown-változatát:

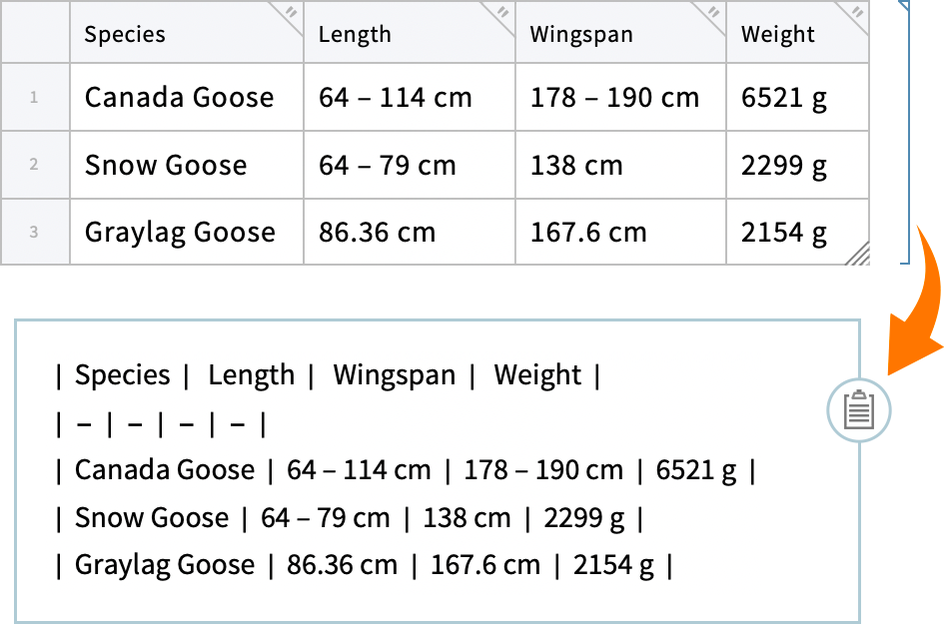
Magától értetődően mindaz, amit a Markdownt interaktívan meg tudsz tenni, programozottan is elérhető a Wolfram Language-ben. Így például az ExportString függvényt használhatod Markdownba történő exportálásra:

 

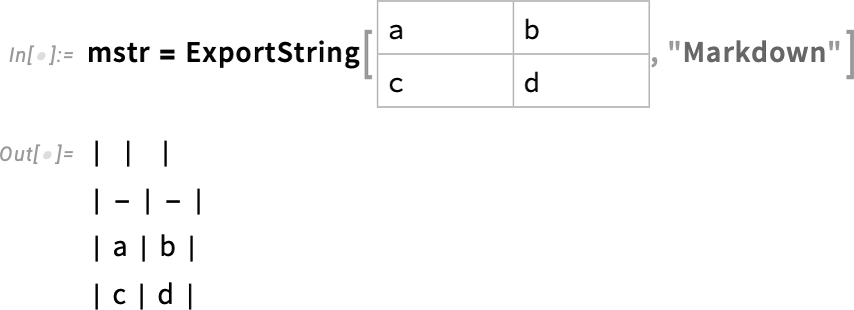
Ennek importálása alapértelmezés szerint sima szöveget ad:

 

De ha azt mondod neki, hogy „formázott szövegként” importálja, akkor táblázatos formában fogja becsomagolni az adatokat:

 

Különösen akkor, amikor LLM-ekkel kommunikálsz, gyakran hasznos, ha vannak Markdown-táblák, amelyek egy hosszabb, eredeti tábla tömör összefoglalói. Itt például azt kérjük, hogy 3 sornyi adat jelenjen meg:

 

És itt azt kérjük, hogy 2 sor az elejéről, valamint 2 sor a végéről jelenjen meg:

 

Számos finomság (és okos heurisztika) kapcsolódik ahhoz, hogy a lehető legjobb — és oda-vissza konvertálható — Markdown készüljön. Ha egy képet Markdown formátumba exportálsz…

…akkor maga a Markdown valójában csak egy hivatkozást tartalmaz egy létrehozott fájlra (az img alkönyvtárban), amelyben a kép van eltárolva. Ez különösen kényelmes a Wolfram Cloud használatakor, ahol a képek adat-URL-ekként vannak beágyazva közvetlenül a Markdown fájlba.

 

 

 

 

 

Újdonság a webes dokumentációban: Navigációs oldalsáv

A 13-as verzió óta van egy választási lehetőség: vagy letöltöd a teljes, 6,5 GB-os Wolfram Language dokumentációt és lokálisan használod, vagy csak a webre hivatkozol, letöltés nélkül. (Egyébként, ha szeretnéd letölteni a dokumentációt, de még nem tetted meg, mindig megteheted a Help > Install Local Documentation menüponttal.)

A 14.3-as verzióban a webes dokumentációban is van egy új funkció: ha a böngésződablak elég széles, minden függvényoldalon megjelenik egy navigációs oldalsáv:

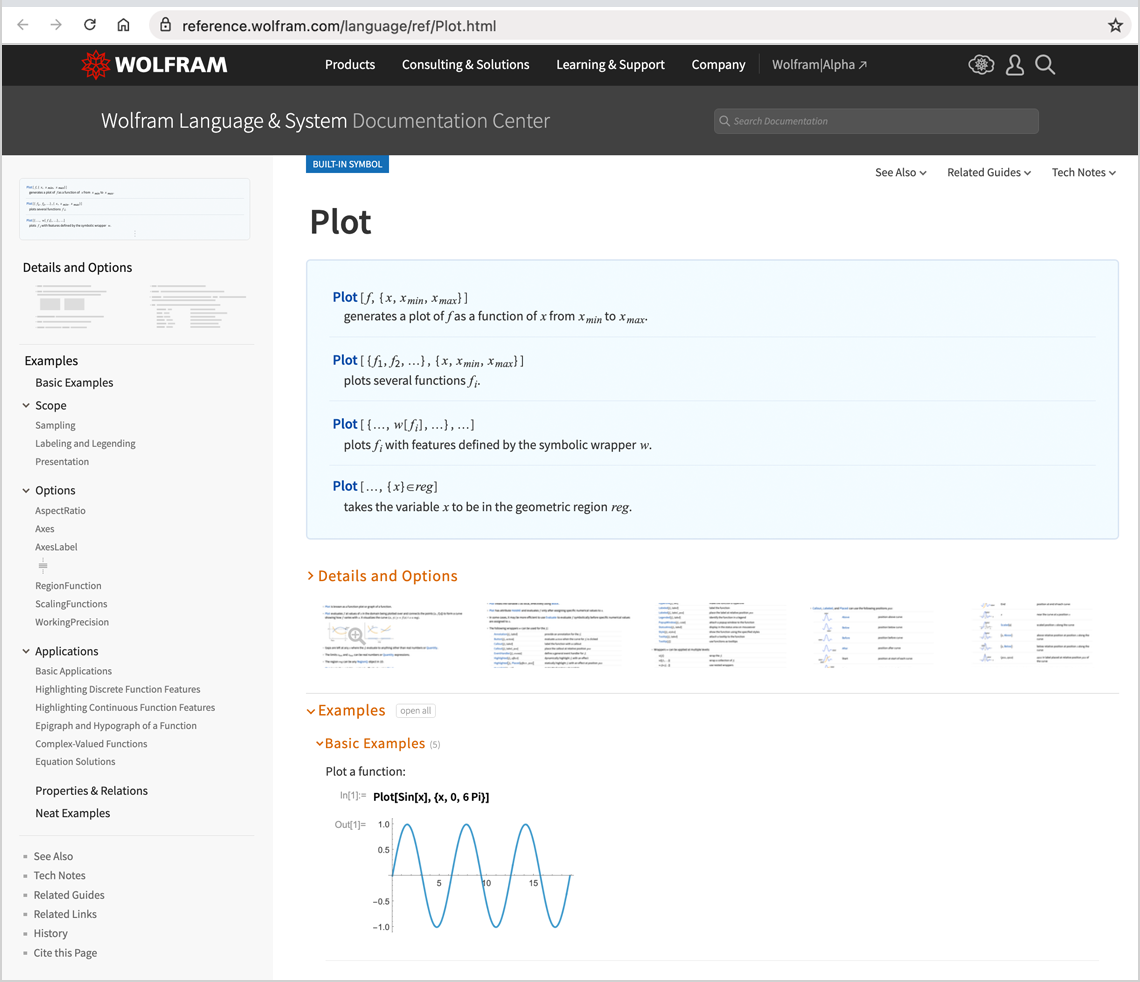
Szeretnéd gyorsan megnézni, hogyan működik az adott opció? Egyszerűen kattints rá az oldalsávban, és az oldal ugrik a megfelelő részhez, megnyitva a kapcsolódó cellákat:

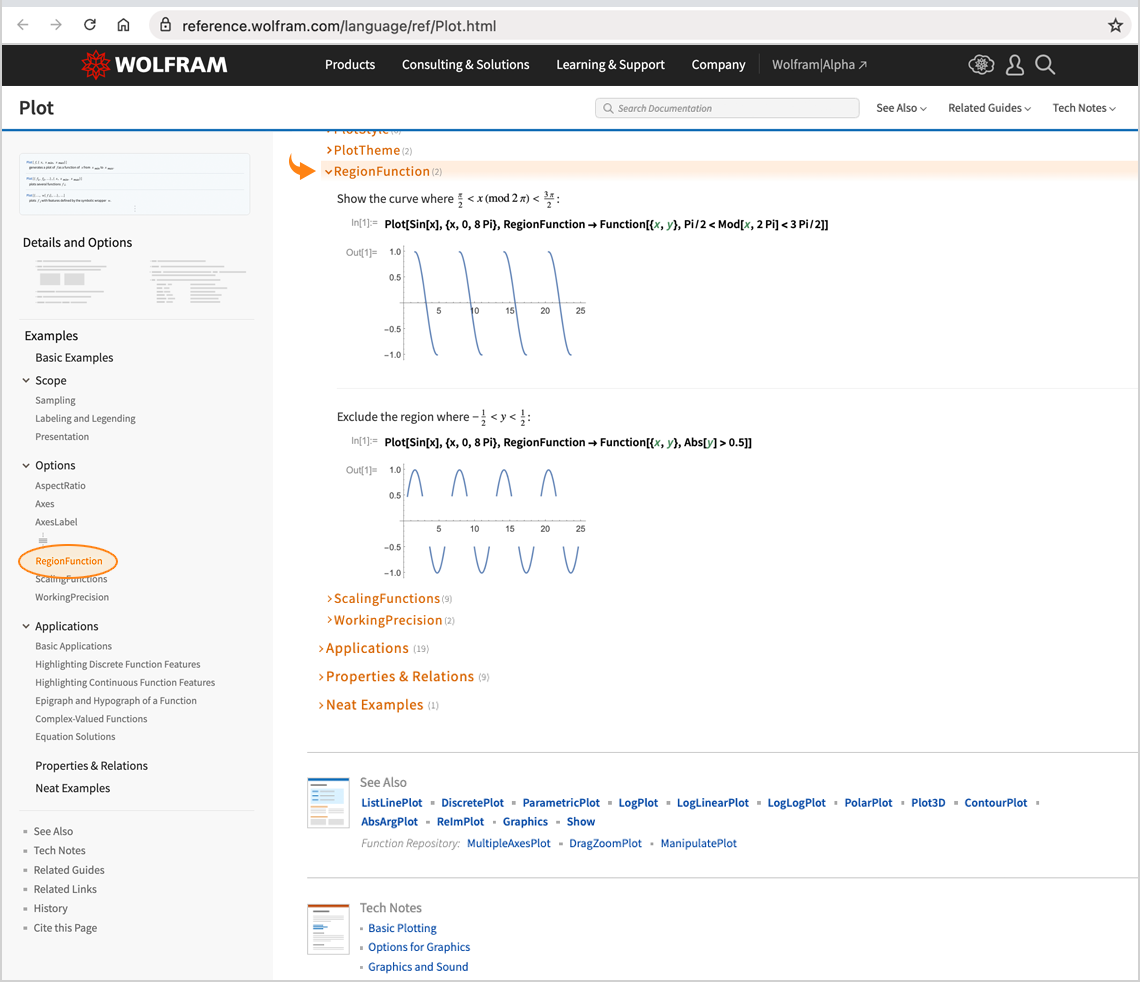
Természetesen, a közel 10 000 oldalas, igen változatos anyagban rengeteg összetett felhasználói élmény (UX) kérdés merül fel. Például a Plot esetében a teljes opciólista nagyon hosszú, ezért alapértelmezés szerint el van rejtve a jelek mögött:

Kattints a jelre, és az összes opció megnyílik — valami hasonlóan, mint egy cellakeret; erre kattintva újra bezárhatod őket:

 

 

 

 

És Még Több…

A 14.3-as verzió egy erős kiadás, tele új képességekkel. És amit eddig átbeszéltünk, az még nem minden — van még további újdonság is.

Videók terén például hozzáadtuk a VideoStabilize funkciót a videók remegésének eltávolítására. A VideoObjectTracking funkciót is fejlesztettük, így most már meghatározott pontokat is követhetsz a videóban. Ha gyakorlatilag minden pontot követni szeretnél, a ImageDisplacements most már videókon is működik.

Képek esetében immár támogatott az .avif (AV1) fájlok importálása.

Beszédszintézisnél mostantól minden művelet helyben, lokálisan történik. A 14.2-es verzióban Mac-en és Windows-on az operációs rendszer alapú beszédszintézist használtuk. Most egy lokális neurális háló modellekből álló gyűjtemény áll rendelkezésre, amely bármely operációs rendszeren következetesen fut — és amikor nem tudunk operációs rendszer alapú beszédszintézist használni, ezek kerülnek alkalmazásra.

A dátumkezelő rendszerünket is tovább csiszoltuk. Új naptípusokat vezettünk be, például „NonHoliday” és „WeekendHoliday”, valamint az operátoros formáját is biztosítjuk a DayMatchQ-nak — mindezek célja, hogy könnyen és nagyon hatékonyan lehessen konkrét dátumtípusokat kiválasztani, különösen a Tabular objektumokban.

Teljesen más területen a RandomTree most sokkal hatékonyabb, és lehetővé teszi megadott csúcsnevekkel rendelkező fák létrehozását — itt például az ábécé szerepel csúcsnevekként:

 

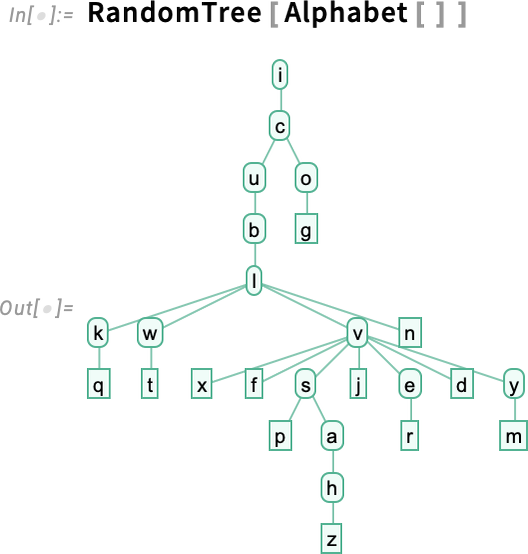
A hatékonyságról szólva, egy kicsi, de hasznos fejlesztés a DataStructure világában, hogy a „BitVector” adatstruktúrák most már többszálas feldolgozást használnak, és a Pick függvény közvetlenül működik ilyen adatstruktúrákon — még azokon is, amelyek milliárdnyi bit hosszúak.

Emellett a GPUArray objektumokkal végzett számításoknál tovább javítottuk az alapvető aritmetikai műveletek teljesítményét, valamint GPU-támogatást adtunk olyan függvényekhez, mint a UnitStep és a NumericalSort.

A részleges differenciálegyenletek (PDE) és a PDE-modellezés folyamatos fejlesztése során a 14.3-as verzió új opciót tartalmaz az axiálisan szimmetrikus folyadékáramlás problémáinak megoldására — lehetővé téve például egy csőszűkületen áthaladó áramlás számítását:

 

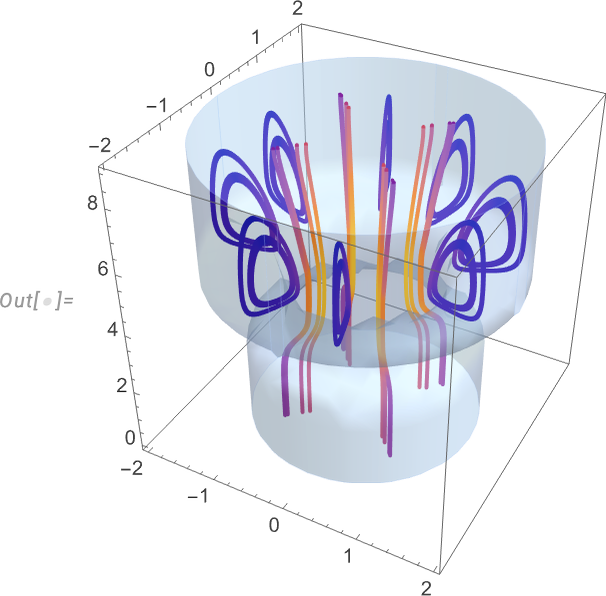
A biokémia területén hozzáadtuk a UniProt és az AlphaFold adatbázisokhoz való kapcsolódást. A kémiában pedig különféle segédfüggvényeket vezettünk be, például a ChemicalFormulaQ és a PatternReactionQ függvényeket.

A fordítóban (compiler) bevezettük a CurrentCompiledFunctionData függvényt, amely lehetővé teszi a fordított függvények introspekcióját — így például megállapíthatod, hogy a fordító milyen konkrét típust rendelt az éppen használt függvényhez:

 

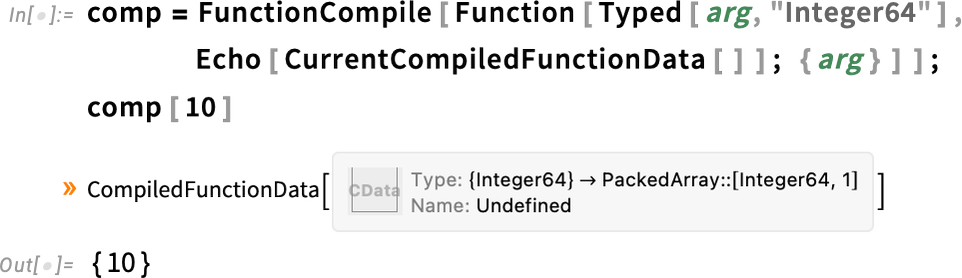
A fordítóban továbbfejlesztettük a DownValuesFunction-t is, hogy lehetővé tegye a „wrap for compilation” használatát olyan függvényeknél, amelyek definíciói Alternatives-hez vagy Except-hez hasonló szerkezeteket tartalmaznak. (Ez egy további előfutára annak, hogy a nyers downvalue hozzárendeléseket közvetlenül lehessen fordítani.)

Mindezek mellett a 14.3-as verzióban rengeteg apró finomítás és simítás került be, valamint több mint ezer hibajavítás — mindezek hozzájárulnak ahhoz, hogy a Wolfram Language használata még gördülékenyebb és gazdagabb élményt nyújtson.

A 14.3-as verzió asztali rendszerekre már letölthető. Emellett ez az a verzió, amelyet automatikusan kapsz a Wolfram Cloud-ban. Tehát… kezd el használni még ma, és tapasztald meg a legújabb intenzív kutatási és fejlesztési munkánk gyümölcsét!