Stata 18 propose la nouvelle commande estat gofplot pour produire des graphiques de qualité d’ajustement (GOF) pour les modèles de survie. Vous pouvez l’utiliser après quatre modèles de survie : le modèle de Cox censuré à droite (stcox), le modèle de Cox censuré par intervalles (stintcox), le modèle paramétrique censuré à droite (streg) et le modèle paramétrique censuré par intervalles (stintreg). Vérifiez l’adéquation du modèle après les modèles stratifiés ou séparément pour chaque sous-groupe.
Les diagrammes GOF permettent de vérifier visuellement l’adéquation du modèle aux données. Dans l’analyse de survie, ces contrôles sont basés sur les résidus dits de Cox-Snell et sur l’hypothèse selon laquelle, si un modèle est correct, ces résidus devraient avoir une distribution exponentielle standard. Visuellement, cette hypothèse est évaluée en traçant les résidus par rapport au risque cumulé estimé – plus les valeurs tracées sont proches de la ligne de 45°, meilleur est l’ajustement (Cox et Snell 1968).
Voyons comment cela fonctionne
Graphiques du GOF pour les données censurées à droite
Nous utilisons l’ensemble de données concernant 103 patients admis au programme de transplantation cardiaque de Stanford (Crowley et Hu 1977). L’ensemble de données comprend l’année où le patient a été accepté dans le programme (année), l’âge du patient (âge), si le patient a subi une autre chirurgie cardiaque auparavant (chirurgie), et si le patient a reçu une transplantation (posttran). Nous souhaitons analyser le temps écoulé jusqu’au décès et vérifier si notre modèle s’adapte bien aux données. Nous ajustons d’abord un modèle de Cox en tapant

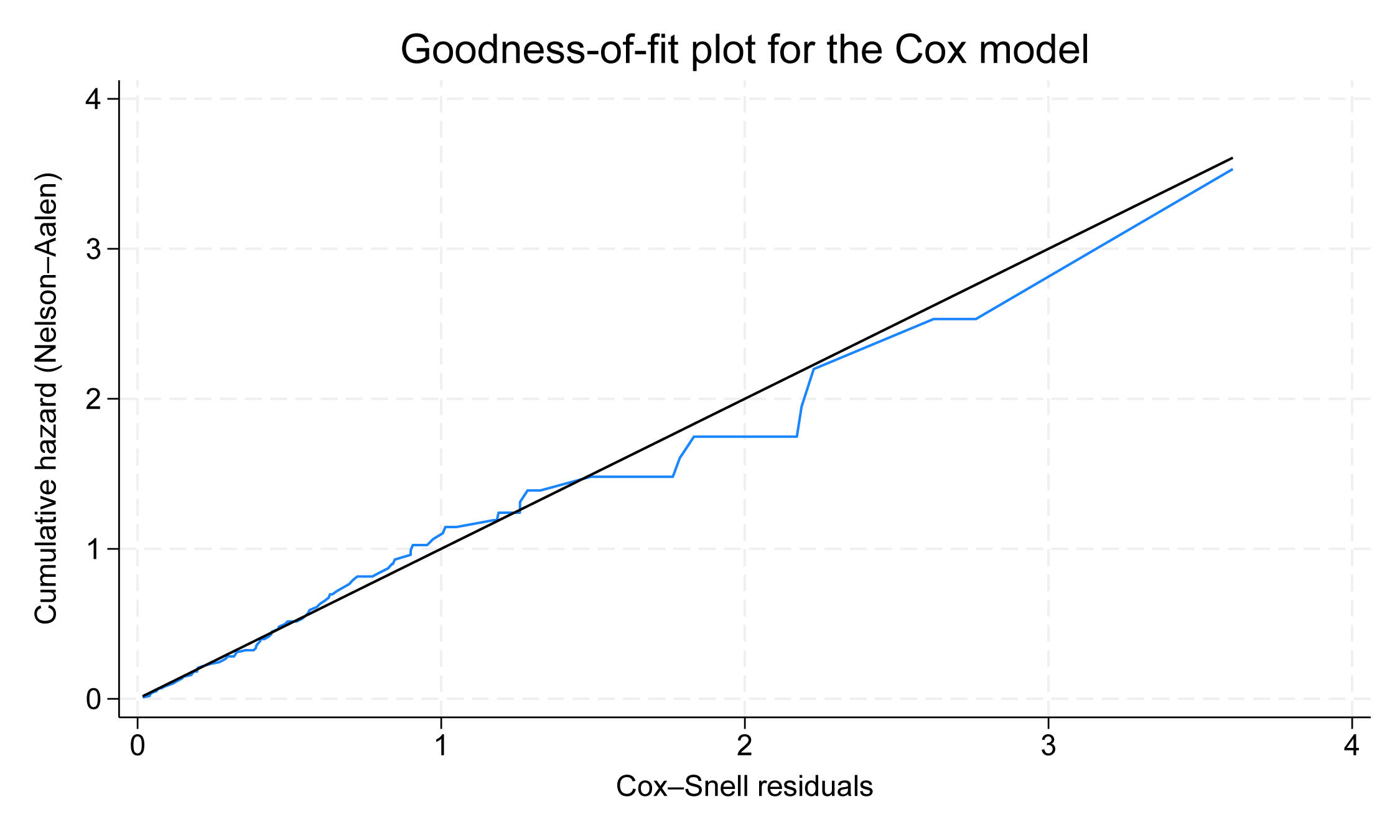
En comparant la ligne bleue à la ligne de référence noire, nous concluons que notre modèle de Cox s’ajuste bien aux données.
Pour les données censurées à droite, au lieu de l’estimateur Nelson-Aalen par défaut (Nelson 1972 ; Aalen 1978), nous pouvons utiliser l’option km pour utiliser le logarithme négatif alternatif de l’estimateur de Kaplan-Meier (Kaplan et Meier 1958).
Ajustons maintenant un modèle de Cox stratifié, qui suppose que les fonctions de risque de base sont différentes entre les patients de différents groupes (pgroup) mais que les coefficients sont égaux dans ces groupes.
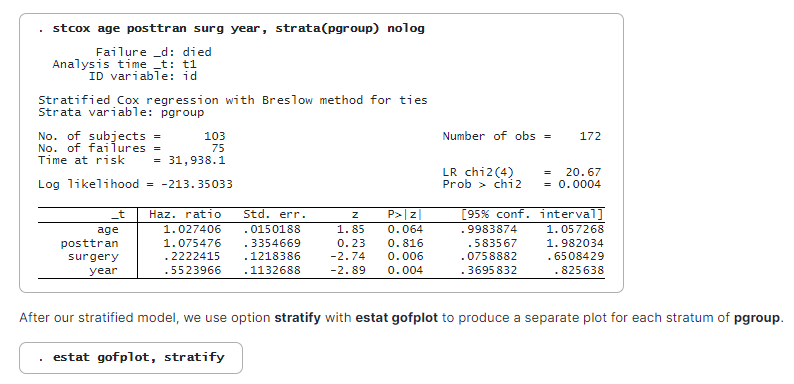
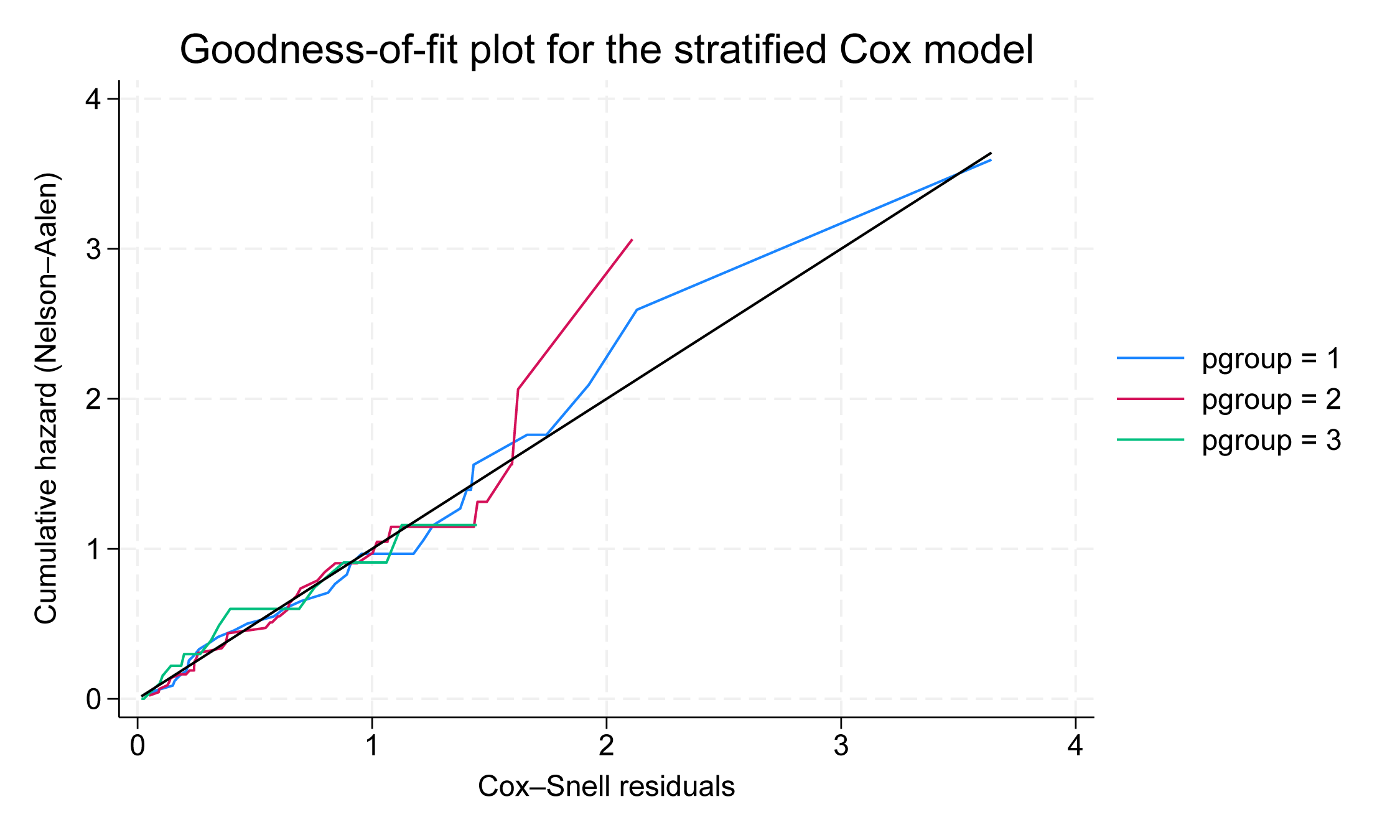
Le modèle s’ajuste bien aux données dans toutes les strates. La ligne rouge pour pgroup = 2 s’écarte de la ligne de référence vers la fin. Il n’est pas rare de voir ce phénomène dans la pratique, car moins d’observations sont disponibles pour l’estimation vers la fin de l’étude.
Pour faciliter l’inspection visuelle du graphique, nous pouvons également ajouter l’option separate pour produire des graphiques distincts pour chaque strate.
. estat gofplot, stratify separate
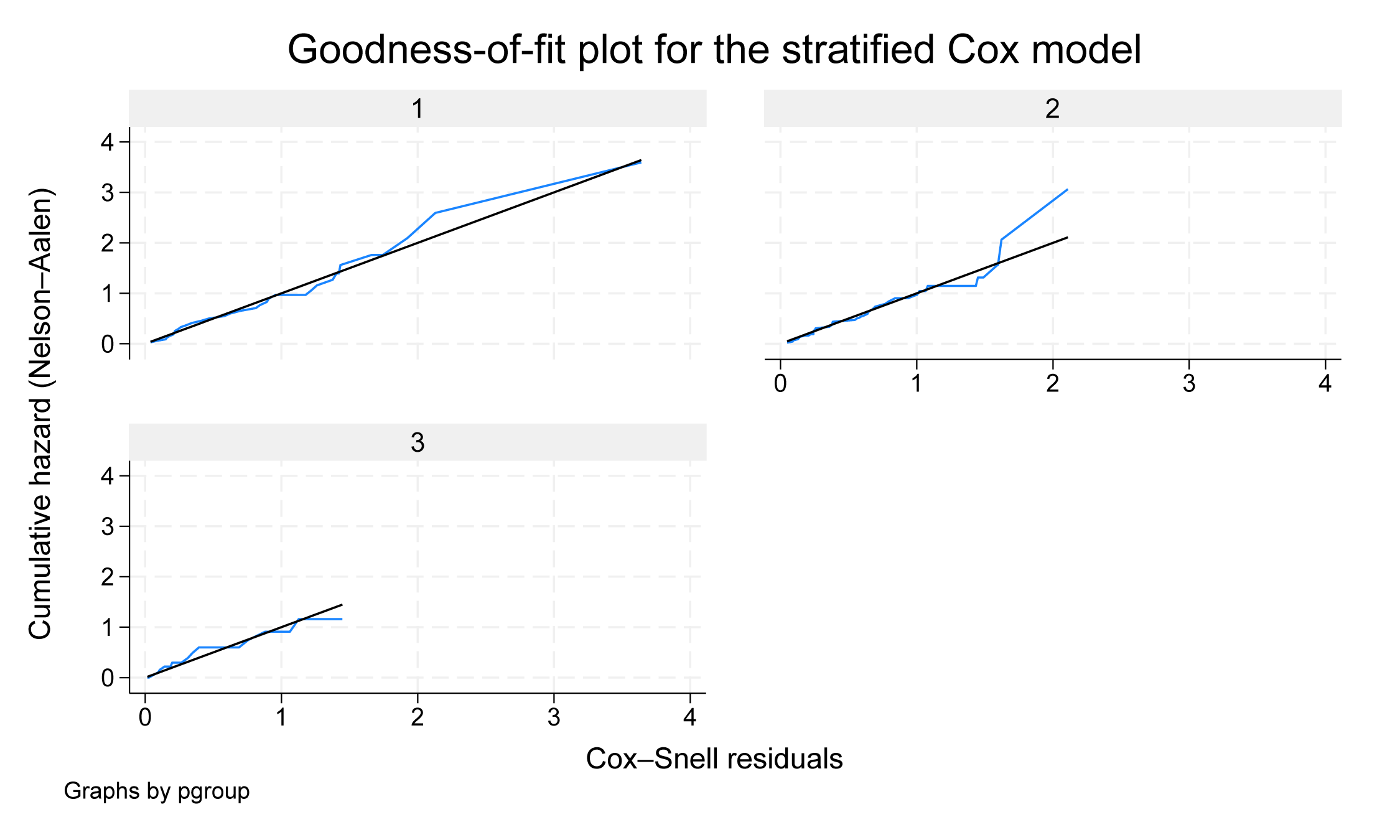
Graphiques du GOF pour les données censurées par intervalles
Nous utilisons l’ensemble des données d’une étude portant sur les patientes atteintes d’un cancer du sein au stade précoce (Finkelstein et Wolfe 1985), qui compare les effets cosmétiques de deux traitements anticancéreux (treat) sur la rétraction des seins. Comme les patientes ont été observées à des moments aléatoires, le moment exact de la rétraction des seins n’a pas été observé et on sait seulement qu’il se situe dans l’intervalle entre les visites (variables ltime et rtime). Tout d’abord, nous avons ajusté un modèle de Weibull censuré par intervalles du temps écoulé avant la rétraction du sein lors du traitement à l’aide de stintreg :

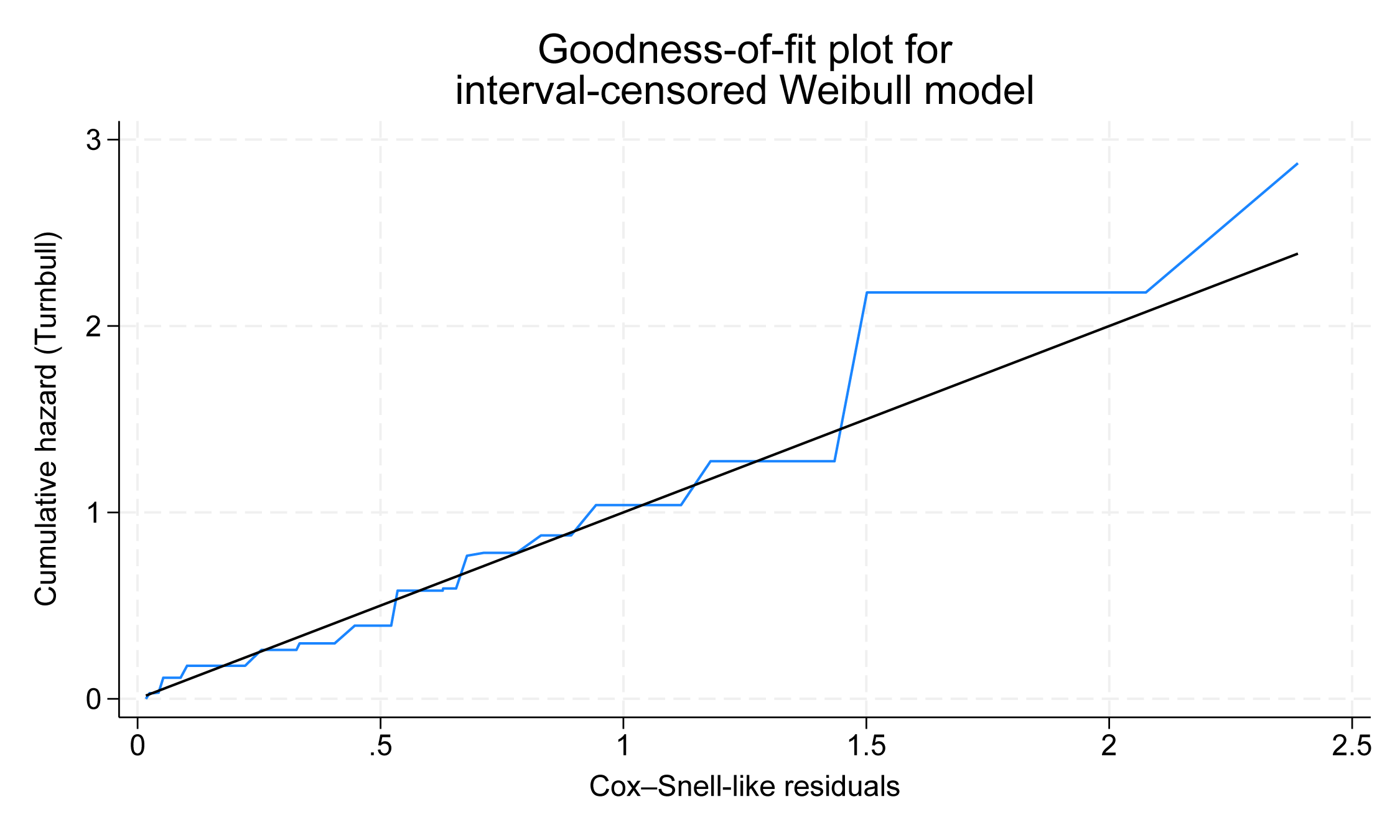
Avec des données censurées par intervalle, des résidus de type Cox-Snell sont définis et utilisés pour le tracé (Farrington 2000). Si un modèle s’ajuste bien aux données, ces résidus devraient se rapprocher de la distribution exponentielle standard censurée. L’estimateur non paramétrique de Turnbull (Turnbull 1976) est également utilisé pour estimer le risque cumulé.
La ligne irrégulière reste proche de la ligne de référence dans le graphique ci-dessus, ce qui indique que le modèle de Weibull s’ajuste bien aux données.
Supposons que nous voulions maintenant ajuster un modèle exponentiel et vérifier son ajustement. Nous tapons
. quietly stintreg i.treat, interval(ltime rtime) distribution(exponential) . estat gofplot
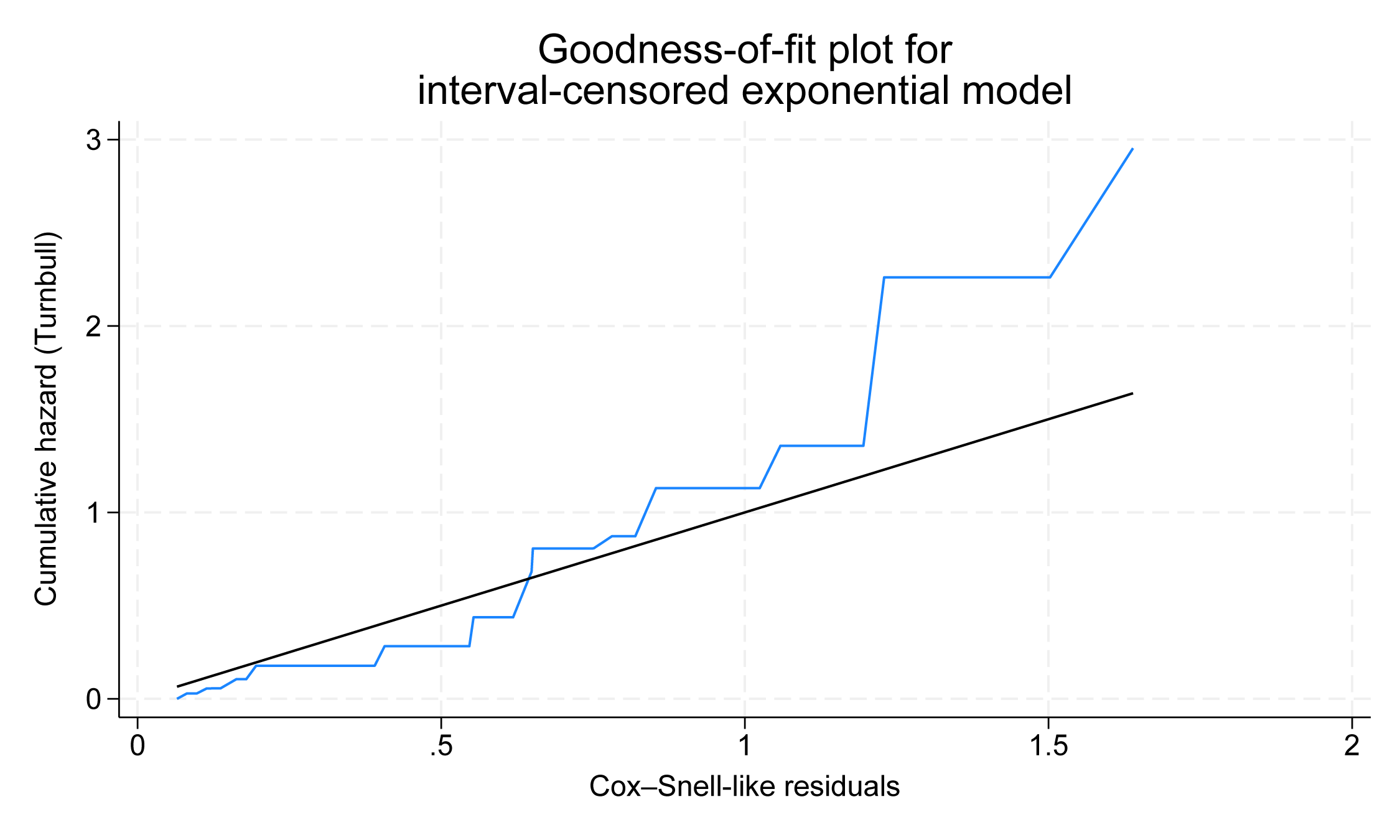
Si l’on compare ce graphique du GOF avec celui ci-dessus, on constate que le modèle de Weibull correspond mieux à nos données que le modèle exponentiel.
Références
Aalen, O. O. 1978. Inférence non paramétrique pour une famille de processus de comptage. Annals of Statistics 6 : 701-726. https://doi.org/10.1214/aos/1176344247.
Cox, D. R., et E. J. Snell. 1968. A general definition of residuals (with discussion). Journal of the Royal Statistical Society, Series B 30 : 248-275.
Crowley, J. et M. Hu. 1977. Covariance analysis of heart transplant survival data. Journal of the American Statistical Association 72 : 27-36.
Farrington, C. P. 2000. Residuals for proportional hazards models with interval-censored survival data. Biometrics 56 : 473-482.
Finkelstein, D. M., et R. A. Wolfe. 1985. A semiparametric model for regression analysis of interval-censored failure time data. Biometrics 41 : 933-945.
Kaplan, E. L., et P. Meier. 1958. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association 53 : 457-481.
Nelson, W. 1972. Theory and applications of hazard plotting for censored failure data. Technometrics 14 : 945-966.
Turnbull, B. W. 1976. The empirical distribution function with arbitrarily grouped, censored and truncated data ». Journal of the Royal Statistical Society, Series B 38 : 290-295.

