Подивимося, як це працює

Ми маємо щоквартальні дані щодо інфляції, розриву випуску та ставки по федеральних фондах.

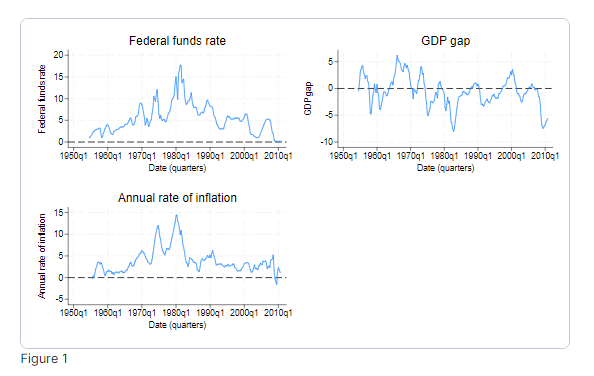
Ми починаємо з оцінки функції імпульсу-відгуку одновимірної моделі розриву випуску.

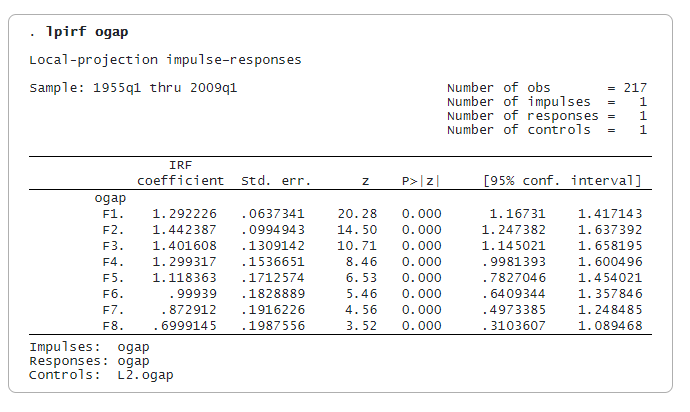
Кожен коефіцієнт є реакцією на імпульс (шок) до розриву випуску на вказану кількість періодів наперед. При ударі ефект шоку дорівнює одиниці. Після одного періоду (F1.ogap) розрив випуску зростає до 1,29. Потім досягає піку в другому періоді на рівні 1,44. Через вісім періодів після шоку реакція падає до 0,70.

Більш цікаві моделі виникають, коли є декілька змінних, і в цьому випадку ми можемо оцінити вплив шоку однієї змінної на іншу. Ми комбінуємо команду lpirf з набором команд irf, щоб оцінити, а потім побудувати графік ортогоналізованих функцій імпульсу-відгуку.

. quietly lpirf inflation ogap fedfunds, lags(1/12) step(24)
. irf set myirfs.irf, replace
. irf create model1
. irf graph oirf, yline(0)

Перший ряд показує реакцію на шок ставки по федеральних фондах, другий – на інфляційний шок, а останній – на шок розриву випуску. Неочікуване підвищення відсоткових ставок призводить до падіння інфляції та випуску протягом наступних кварталів, причому реакція інфляції досягає дна приблизно через 12 кроків (3 роки) після імпульсу, а реакція випуску досягає дна приблизно через 8 кроків (2 роки) після імпульсу. Інфляційний шок штовхає інфляцію та випуск в протилежних напрямках, а процентна ставка у відповідь помірно зростає. Шок випуску призводить до зростання як інфляції, так і процентної ставки.

Давайте подивимося, як це працює ще раз

У цьому прикладі ми маємо щомісячний набір даних про логарифм індексу промислового виробництва, логарифм індексу споживчих цін та показник екзогенних монетарних шоків з роботи Ромера та Ромера (2004) та оновлений у роботі Віланда та Яна (2020).

Нас цікавить реакція промислового виробництва та інфляції на монетарний шок. Ми вважаємо промислове виробництво та інфляцію ендогенними, а монетарний шок – екзогенним. Ми використовуємо дві моделі: модель локального прогнозування та модель векторної авторегресії (VAR).

. irf set comparemodels.irf, replace
. quietly lpirf indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create lpmodel
. quietly var indpro inflation, lags(1/12) exog(L(0/12).money_shock)
. irf create varmodel
. irf graph dm, impulse(money_shock) irf(lpmodel varmodel)

Динамічні мультиплікатори з локально-проекційної та VAR моделей є

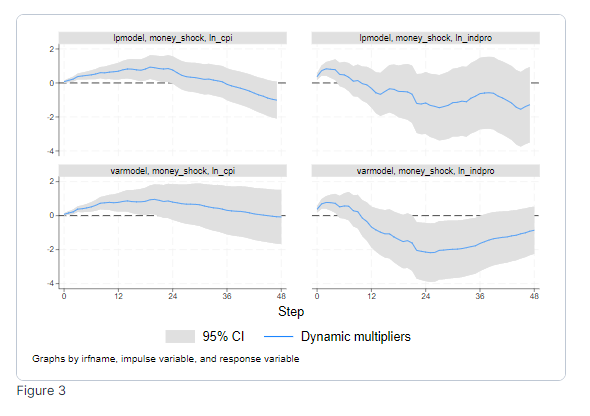
У верхньому рядку наведено результати моделі локального прогнозування. У нижньому рядку показано результати VAR моделі, в якій грошовий шок розглядається як екзогенний.

Як модель локального прогнозування, так і VAR модель показують незначне зростання рівня цін після монетарного шоку, що досягає піку приблизно через 24 місяці після шоку і далі знижується. Обидві моделі показують, що промислове виробництво падає після монетарного шоку, причому пік падіння настає приблизно через 24 місяці після шоку. Локальні прогнози ВРЦ та ВРЦ моделі VAR дають подібні результати на коротких горизонтах, але починають розходитись на довших горизонтах. Локальні прогнози забезпечують більшу гнучкість у довгострокових реакціях, оскільки оцінюють їх безпосередньо. Крім того, локальні прогнози обчислюються набагато швидше.

Посилання

Ромер, К. Д. та Д. Х. Ромер. 2004. Новий вимірник монетарних шоків: Виведення та наслідки. Американський економічний огляд 94: 1055-1084.

Віланд, Я. Ф. та М. Янг. 2020. Фінансове демпфування. Журнал грошей, кредиту та банківської справи 52: 79-113.