New In 
Байєсівське усереднення моделі (BMA) для лінійної регресії
Навіщо обирати лише одну модель, якщо можна запозичити інформацію з багатьох? Новий пакет bma виконує байєсівське усереднення моделі, щоб врахувати невизначеність моделі у вашому аналізі. Не знаєте, які предиктори включити у вашу модель лінійної регресії? Скористайтеся bmaregress, щоб дізнатися, які предиктори є важливими. Зробіть вибір моделі, висновок і прогноз. Використовуйте багато команд пост-оцінки, щоб дослідити впливові моделі, складність моделі, відповідність моделі та прогностичні характеристики, аналіз чутливості до припущень про важливість моделей та предикторів тощо.
Основні моменти
Вибір моделі, висновки та прогнозування
Перепис моделей та вибірка MC3
Завжди включені та згруповані предиктори
Моделі попередніх подій: рівномірна, біноміальна, бета-біноміальна
Багато g-пріорів, включаючи гіпер-g та robust
Факторні змінні та оператори часових рядів
Сильна, слабка або відсутня спадковість для взаємодії
Конвергенція BMA MCMC
Апостеріорна модель та ймовірності включення
Попередній та апостеріорний розподіл розміру моделі
Апостеріорні розподіли параметрів моделі
Міри спільності для пар предикторів
Карти включення змінних
Журналізуйте прогнозний бал для оцінки відповідності моделі та ефективності прогнозування
Аналіз чутливості
Прогнозування
Підтримка стандартних функцій байєсівського постоцінювання
Побачити більше Усереднення байєсівської моделі особливості
Вступ
Традиційно ми обираємо модель і робимо висновки та прогнози на основі цієї моделі. Наші результати, як правило, не враховують невизначеність у виборі моделі і тому можуть бути надто оптимістичними. Вони навіть можуть бути неправильними, якщо обрана нами модель суттєво відрізняється від справжньої моделі, що генерує дані (МГД). У деяких додатках ми можемо мати переконливі теоретичні або емпіричні докази щодо DGM. В інших додатках, зазвичай складних і нестабільних за своєю природою, таких як економіка, психологія та епідеміологія, вибір однієї надійної моделі може бути складним. Замість того, щоб покладатися лише на одну модель, модельне усереднення усереднює результати за кількома правдоподібними моделями, заснованими на спостережуваних даних. У BMA “правдоподібність” моделі описується апостеріорною ймовірністю моделі (PMP), яка визначається за допомогою фундаментальних байєсівських принципів – теореми Байєса – і застосовується універсально до всіх аналізів даних. БМА можна використовувати для врахування невизначеності моделі при оцінюванні параметрів моделі та прогнозуванні нових спостережень, щоб уникнути надмірно оптимістичних висновків. Він особливо корисний у випадках, коли є кілька правдоподібних моделей, і немає жодної остаточної причини для вибору певної моделі над іншими. Але навіть якщо вибір однієї моделі є кінцевою метою, ви можете знайти BMA корисним. Він забезпечує принциповий спосіб виявлення важливих моделей і предикторів у розглянутих класах моделей. Його структура дозволяє дізнатися про взаємозв’язки між різними предикторами з точки зору їхньої тенденції з’являтися в моделі разом, окремо або незалежно. Він може бути використаний для оцінки чутливості кінцевих результатів до різних припущень про важливість різних моделей і предикторів. Він забезпечує оптимальні прогнози в сенсі лог-балів.
Набір bma
У регресії невизначеність моделі дорівнює невизначеності того, які предиктори слід включити в модель. Ми можемо використовувати bmaregress, щоб врахувати вибір предикторів у лінійній регресії. Він досліджує простір моделі або вичерпно з опцією перебору, коли це можливо, або за допомогою алгоритму композиції моделі ланцюгового Монте-Карло (MCMC) (MC3) з опцією вибірки. Він надає різні зведення про переглянуті моделі та включені предиктори, а також про апостеріорні розподіли параметрів моделі. Дозволяє вказати групи предикторів, які потрібно включити або виключити з моделі разом, а також ті, які включаються в усі моделі. Він надає різні попередні розподіли для моделей в опції mprior() і для параметра g, який контролює зсув коефіцієнтів регресії до нуля, в опції gprior(). Він також підтримує факторні змінні та оператори часових рядів і надає кілька способів обробки взаємодій під час оцінювання за допомогою опції heredity().
Існує багато підтримуваних функцій постобчислення, які також включають деякі стандартні функції байєсівського постобчислення.
| Командир | Опис |
|---|---|
Апостеріорні вибірки коефіцієнтів регресії | |
модельно-імовірнісні графіки | |
графіки розподілу за розміром моделі | |
карти включення змінних | |
графіки апостеріорної щільності коефіцієнтів | |
апостеріорна модель та підсумки включення змінних | |
зведення про розмір моделі | |
апостеріорні ймовірності включення (PIP) для предикторів | |
міри спільності для предикторів | |
log predictive-score (LPS) | |
Прогнози BMA | |
Байєсівські графічні зведення та діагностика збіжності | |
Байєсівська підсумкова статистика для параметрів моделі та їх функцій | |
Байєсівський ефективний розмір вибірки та пов’язані з ним статистики | |
Байєсівські прогнозні p-значення | |
Байєсівські прогнози |
Нижче ми розглянемо деякі можливості bma на прикладі іграшкового набору даних. Цей набір даних містить n=200
�=200 спостережень, p=10 �=10 ортогональних предикторів та результат y, згенерований як
y=0.5+1.2×x2+5×x10+ϵ
�=0.5+1.2�2+5�10+�
де ϵ∼N(0,1)
�∼�(0,1) – стандартна нормальна похибка.
. webuse bmaintro (Simulated data for BMA example) . summarize
| Variable | Obs Mean Std. dev. Min Max | |
| y | 200 .9944997 4.925052 -13.332 13.06587 | |
| x1 | 200 -.0187403 .9908957 -3.217909 2.606215 | |
| x2 | 200 -.0159491 1.098724 -2.999594 2.566395 | |
| x3 | 200 .080607 1.007036 -3.016552 3.020441 | |
| x4 | 200 .0324701 1.004683 -2.410378 2.391406 | |
| x5 | 200 -.0821737 .9866885 -2.543018 2.133524 | |
| x6 | 200 .0232265 1.006167 -2.567606 3.840835 | |
| x7 | 200 -.1121034 .9450883 -3.213471 1.885638 | |
| x8 | 200 -.0668903 .9713769 -2.871328 2.808912 | |
| x9 | 200 -.1629013 .9550258 -2.647837 2.472586 | |
| x10 | 200 .083902 .8905923 -2.660675 2.275681 | |
Перерахування моделей
Ми використовуємо bmaregress, щоб підігнати лінійну регресію BMA для y від x1 до x10.
. bmaregress y x1-x10
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 200
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Beta-binomial(1, 1) For CPMP >= .9 = 9
Cons.: Noninformative Mean model size = 2.479
Coef.: Zellner's g
g: Benchmark, g = 200 Shrinkage, g/(1+g) = 0.9950
sigma2: Noninformative Mean sigma2 = 1.272| y | Mean Std. dev. Group PIP | |
| x2 | 1.198105 .0733478 2 1 | |
| x10 | 5.08343 .0900953 10 1 | |
| x3 | -.0352493 .0773309 3 .21123 | |
| x9 | .004321 .0265725 9 .051516 | |
| x1 | .0033937 .0232163 1 .046909 | |
| x4 | -.0020407 .0188504 4 .039267 | |
| x5 | .0005972 .0152443 5 .033015 | |
| x9 | -.0005639 .0153214 8 .032742 | |
| x7 | -8.23e-06 .015497 7 .032386 | |
| x6 | -.0003648 .0143983 6 .032361 | |
| Always | ||
| _cons | .5907923 .0804774 0 1 | |
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default priors are used for models and parameter g.
З 10 предикторами та фіксованим (еталонним) g-пріоритетом за замовчуванням, bmaregress використовує перебір моделей і досліджує всі 210=1 024
210=1,024 можливі моделі. За замовчуванням використовується бета-біноміальна модель з параметрами форми 1, яка є рівномірною за розміром моделі. Апріорі наша БМА-модель припускала незначне спадання коефіцієнтів регресії до нуля, оскільки g/(1+g)=0.9950 �/(1+�)=0.9950 є близьким до 1.
bmaregress визначив x2 та x10 як дуже важливі предиктори – їхні апостеріорні ймовірності включення (PIP) практично дорівнюють 1. Середні апостеріорні оцінки їхніх коефіцієнтів регресії становлять, відповідно, 1,2 (округлено) та 5,1 і є дуже близькими до істинних значень 1,2 та 5. Всі інші предиктори мають значно нижчі ПІП та оцінки коефіцієнтів, близькі до нуля. Наші результати БМА узгоджуються з істинним ДГМ.
Збережемо наші поточні результати оцінювання для подальшого використання. Як і у випадку з іншими байєсівськими командами, ми повинні спочатку зберегти результати моделювання, перш ніж ми зможемо використати сховище оцінок для зберігання результатів оцінювання.
. bmaregress, saving(bmareg) note: file bmareg.dta saved. . estimates store bmareg
Довірчі інтервали
За замовчуванням bmaregress не показує довірчі інтервали (ДІ), оскільки це вимагає потенційно трудомісткого моделювання апостеріорної вибірки параметрів моделі. Але ми можемо обчислити їх після оцінювання.
Спочатку ми використовуємо bmacoefsample для генерації вибірки MCMC з апостеріорного розподілу параметрів моделі, які включають коефіцієнти регресії. Потім ми використовуємо існуючу команду bayesstats summary для обчислення апостеріорних підсумків згенерованої вибірки MCMC.
. bmacoefsample, rseed(18) Simulation (10000): ....5000....10000 done . bayesstats summary Posterior summary statistics MCMC sample size = 10,000
| Equal-tailed | ||
| Mean Std. dev. MCSE Median [95% cred. interval] | ||
| y | ||
| x1 | .0031927 .0234241 .000234 0 0 .0605767 | |
| x2 | 1.197746 .0726358 .000735 1.197211 1.053622 1.341076 | |
| x3 | -.0361581 .0780037 .00078 0 -.2604694 0 | |
| x4 | -.0021015 .018556 .000186 0 -.0306376 0 | |
| x5 | .0004701 .0147757 .000148 0 0 0 | |
| x6 | -.0003859 .0140439 .000142 0 0 0 | |
| x7 | -.0003311 .0166303 .000166 0 0 0 | |
| x8 | -.0005519 .0145717 .00015 0 0 0 | |
| x9 | .0046535 .0273899 .000274 0 0 .096085 | |
| x10 | 5.08357 .0907759 .000927 5.083466 4.90354 5.262716 | |
| _cons | .5901334 .0811697 .000801 .5905113 .4302853 .7505722 | |
| sigma2 | 1.272579 .1300217 .0013 1.262612 1.043772 1.555978 | |
| g | 200 0 0 200 200 200 | |
95% ДІ для коефіцієнта x2 становить [1,05, 1,34], а для x10 – [4,9, 5,26], що узгоджується з нашою ММР.
Впливові моделі
Оцінки коефіцієнта BMA усереднені для 1024 моделей. Важливо дослідити, які моделі є впливовими. Ми можемо використати моделі bmastats для дослідження ПМП.
. bmastats models
Model summary Number of models:
Visited = 1,024
Reported = 5
Analytical PMP Model size .6292 2 .1444 3 .0258 3 .0246 3 .01996 3
| Rank | 1 | 2 | 3 | 4 | 5 | |||||||
Variable-inclusion summary
| Rank Rank Rank Rank Rank | |||||
| 1 2 3 4 5 | |||||
| x2 | x x x x x | ||||
| x10 | x x x x x | ||||
| x3 | x | ||||
| x9 | x | ||||
| x1 | x | ||||
| x4 | x | ||||
Legend: x - estimated
Не дивно, що модель, яка містить як x2, так і x10, має найвищий ПМП – близько 63%. Насправді, дві найкращі моделі відповідають кумулятивній ЧПС близько 77%:
. bmastats models, cumulative(0.75)
Computing model probabilities ...
Model summary Number of models:
Visited = 1,024
Reported = 2| Analytical CPMP Model size | ||
| Rank | ||
| 1 | .6292 2 | |
| 2 | .7736 3 | |
Variable-inclusion summary
| Rank Rank | |||||
| 1 2 | |||||
| x2 | x x | ||||
| x10 | x x | ||||
| x3 | x | ||||
Legend: x - estimated
Ми можемо використати bmagraph pmp для побудови графіку кумулятивного PMP.
. bmagraph pmp, cumulative

За замовчуванням команда будує перші 100 моделей, але ви можете вказати опцію top(), якщо хочете побачити більше моделей.
Важливі предиктори
Ми можемо дослідити важливість предикторів візуально, використовуючи bmagraph varmap для створення карти включення змінних.
. bmagraph varmap Computing model probabilities ...

x2 та x10 входять до всіх 100 найкращих моделей, ранжованих за PMP. Їх коефіцієнти є додатними в усіх моделях.
Розподіл розмірів моделі
Ми можемо дослідити складність нашої BMA-моделі, використовуючи bmastats msize та bmagraph msize для дослідження попереднього та наступного розподілів розміру моделі.
. bmastats msize Model-size summary Number of models = 1,024 Model size: Minimum = 0 Maximum = 10
| Mean Median | |||||
| Prior | |||||
| Analytical | 5.0000 5 | ||||
| Posterior | |||||
| Analytical | 2.4794 2 | ||||
Note: Frequency summaries not available.
. bmagraph msize
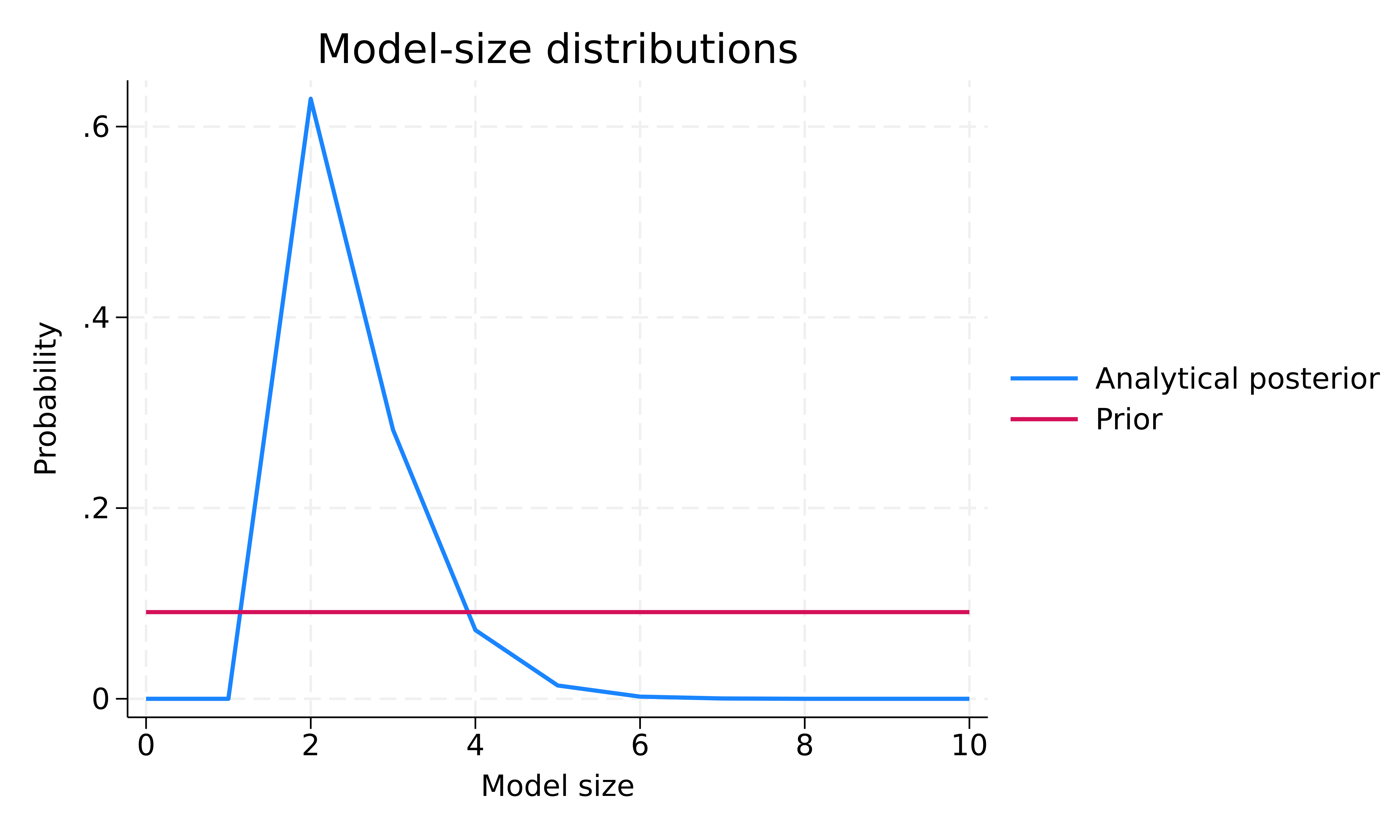
Попередній розподіл розмірів моделей є рівномірним за розміром моделі. Апостеріорний розподіл моделей за розміром зміщений вліво з модою близько 2. Попередній середній розмір моделі становить 5, а апостеріорний – 2,48. Отже, виходячи зі спостережених даних, BMA надає перевагу меншим моделям з приблизно двома предикторами в середньому, порівняно з нашим апріорним припущенням.
Апостеріорні розподіли коефіцієнтів
Ми можемо використати bmagraph coefdensity для побудови апостеріорних розподілів коефіцієнтів регресії.
. bmagraph coefdensity {x2} {x3}, combine
Ці розподіли є сумішшю точкової маси в нулі, що відповідає ймовірності невключення предиктора, і неперервної щільності, зумовленої включенням. Для коефіцієнта x2 ймовірність невключення є незначною, тому його апостеріорний розподіл є неперервною, досить симетричною щільністю з центром в точці 1,2. Для коефіцієнта x3, на додаток до умовної неперервної щільності, існує червона вертикальна лінія в нулі, що відповідає апостеріорній ймовірності невключення приблизно 1-.2 = 0.8.
Прогнозування BMA
bmapredict створює різні прогнози BMA. Наприклад, обчислимо апостеріорне прогностичне значення.
. bmapredict pmean, mean note: computing analytical posterior predictive means.
Ми також можемо обчислити прогнозні CRI, щоб оцінити невизначеність наших прогнозів. (Це недоступно для багатьох традиційних методів вибору моделі.) Зауважте, що ці прогнозні CrI також включають невизначеність моделі. Щоб обчислити прогнозні CrI, ми повинні спочатку зберегти апостеріорну вибірку параметрів моделі MCMC.
. bmacoefsample, saving(bmacoef)
note: saving existing MCMC simulation results without resampling; specify
option simulate to force resampling in this case.
note: file bmacoef.dta saved.
. bmapredict cri_l cri_u, cri rseed(18)
note: computing credible intervals using simulation.
Computing predictions ...
Підбиваємо підсумки прогнозованих результатів:
. summarize y pmean cri*
| Variable | Obs Mean Std. dev. Min Max | ||||
| y | 200 .9944997 4.925052 -13.332 13.06587 | ||||
| pmean | 200 .9944997 4.783067 -13.37242 12.31697 | ||||
| cri_l | 200 -1.24788 4.787499 -15.66658 10.03054 | ||||
| cri_u | 200 3.227426 4.779761 -11.06823 14.58301 | ||||
Наведені середні значення за спостереженнями для прогнозних середніх, а також нижня та верхня 95% межі прогнозного CrI виглядають обґрунтованими відносно спостережуваного результату y.
Інформативні судимості моделі
Однією з сильних сторін БМА є можливість врахування попередньої інформації про моделі та предиктори. Це дозволяє дослідити чутливість результатів до різних припущень про важливість моделей і предикторів. Припустимо, що ми маємо достовірну інформацію про те, що всі предиктори, окрім x2 та x10, з меншою ймовірністю пов’язані з результатом. Ми можемо вказати, наприклад, біноміальну модель з низькою попередньою ймовірністю включення для цих предикторів.
Щоб пізніше порівняти ефективність моделей BMA поза вибіркою, ми випадковим чином розділили нашу вибірку на дві частини і підібрали модель BMA, використовуючи першу підвибірку. Ми також зберегли результати цієї більш інформативної моделі BMA.
. splitsample, generate(sample) nsplit(2) rseed(18)
. bmaregress y x1-x10 if sample == 1, mprior(binomial x2 x10 0.5 x1 x3-x9 0.05)
saving(bmareg_inf)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 10
Always = 0
Priors: No. of models = 1,024
Models: Binomial, IP varies For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 2.072
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.268
| y | Mean Std. dev. Group PIP | |||
| x2 | 1.168763 .1031096 2 1 | |||
| x10 | 4.920726 .124615 10 1 | |||
| x1 | .0019244 .0204242 1 .013449 | |||
| x5 | -.0018262 .0210557 5 .011973 | |||
| x3 | -.0017381 .0205733 3 .011557 | |||
| x4 | -.0015444 .0193858 4 .010709 | |||
| Always | ||||
| _cons | .5637673 .113255 0 1 | |||
Note: Coefficient posterior means and std. dev. estimated from 1,024 models. Note: Default prior is used for parameter g. Note: 4 predictors with PIP less than .01 not shown. file bmareg_inf.dta saved. . estimates store bmareg_inf
Наслідком такого попереднього врахування моделі є те, що PIP всіх неважливих предикторів тепер менше 2%.
Зауважте, що коли ми обираємо одну модель, ми, по суті, підганяємо модель BMA з дуже сильним попереднім значенням, що всі обрані предиктори мають бути включені з ймовірністю 1. Наприклад, ми можемо змусити bmaregress включити всі змінні в модель:
. bmaregress y (x1-x10, always) if sample == 1, saving(bmareg_all)
Enumerating models ...
Computing model probabilities ...
Bayesian model averaging No. of obs = 100
Linear regression No. of predictors = 10
Model enumeration Groups = 0
Always = 10
Priors: No. of models = 1
Models: Beta-binomial(1, 1) For CPMP >= .9 = 1
Cons.: Noninformative Mean model size = 10.000
Coef.: Zellner's g
g: Benchmark, g = 100 Shrinkage, g/(1+g) = 0.9901
sigma2: Noninformative Mean sigma2 = 1.192
Mean Std. dev. Group PIP
.1294521 .105395 0 1
1.166679 .1129949 0 1
-.1433074 .1271903 0 1
-.1032189 .1223152 0 1
-.0819008 .1261309 0 1
.0696633 .1057512 0 1
.0222949 .1215404 0 1
-.0252311 .1124352 0 1
.0587412 .1166921 0 1
4.949992 .1276795 0 1
.6006153 .1127032 0 1
| y | Always | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | _cons | ||||||||||||
Note: Coefficient posterior means and std. dev. estimated from 1 model. Note: Default priors are used for models and parameter g. file bmareg_all.dta saved. . estimates store bmareg_all
Прогнозування продуктивності за допомогою LPS
Для порівняння розглянутих моделей ВМР ми модифікуємо нашу стандартну модель ВМР, використовуючи першу підвибірку, і зберігаємо результати оцінювання.
. qui bmaregress y x1-x10 if sample == 1, saving(bmareg, replace) . estimates store bmareg
Ми можемо порівняти позавибіркову прогностичну ефективність наших моделей BMA, використовуючи bmastats lps для обчислення log predictive-score (LPS) для позавибіркових спостережень.
. bmastats lps bmareg bmareg_inf bmareg_all if sample == 2, compact Log predictive-score (LPS) Number of observations = 100
| LPS | Mean Minimum Maximum | ||||
| bmareg | 1.562967 1.039682 6.778834 | ||||
| bmareg_inf | 1.562238 1.037576 6.883794 | ||||
| bmareg_all | 1.576231 1.032793 6.084414 | ||||
Notes: Using analytical PMPs.
Result bmareg_inf has the smallest mean LPS.
Більш інформативна модель bmareg_inf має дещо менше середнє значення LPS, але зведення LPS для всіх моделей дуже схожі. Дивіться [BMA] bmastats lps про те, як порівняти ефективність моделей BMA за допомогою перехресної перевірки.
Прибирання
Під час аналізу ми створили кілька наборів даних. Вони нам більше не потрібні, тому в кінці ми їх видалимо. Але ви можете вирішити зберегти їх, особливо якщо вони відповідають потенційно трудомісткому фінальному аналізу.
. erase bmareg.dta . erase bmacoef.dta . erase bmareg_inf.dta . erase bmareg_all.dta
