Обзор

Новая команда reri оценивает аддитивные взаимодействия в биномиальных обобщенных линейных моделях, логистической, пуассоновской и отрицательной биномиальной регрессиях, а также в моделях выживания Кокса и других.

Двусторонние взаимодействия в моделях, оценивающих RR, обычно выражаются в виде мультипликативных взаимодействий. Однако для многих биологических процессов аддитивная модель взаимодействия может моделировать процесс лучше, чем мультипликативная (см., например, Andersson et al. [2005]).

Для бинарных воздействий A и B мы часто хотим смоделировать риск положительного исхода для испытуемых, имевших и A, и B, по сравнению с испытуемыми, имевшими только A, и испытуемыми, имевшими только B. То есть мы хотим исследовать взаимодействие A и B.

В мультипликативной модели риск для испытуемых с A и B предположительно равен риску только для A, умноженному на риск только для B. Если риск для A и B равен мультипликативному риску, мы говорим, что взаимодействия A и B нет. Если риск больше мультипликативного риска, мы говорим, что есть положительное взаимодействие. Мультипликативные модели удобны тем, что их просто задать, и легко проверить, является ли взаимодействие больше (или меньше) мультипликативного.

В аддитивной модели риск для субъектов с A и B, согласно гипотезе, равен риску только для A плюс риск только для B. Для этой гипотезы мы хотим посмотреть, насколько риск для A и B больше (или меньше) аддитивного риска.

Статистика RERI — это разница рисков, сформулированная с помощью RR (Rothman, Greenland, and Lash 2008). Значение статистики RERI, равное 0, означает, что риск аддитивен. Положительная статистика RERI означает, что риск является супераддитивным, а отрицательная — субаддитивным. Тест на статистическую значимость статистики RERI прост, но не так прост, как тест для мультипликативной модели.

Кроме статистики RERI, команда reri выдает еще две связанные с ней статистики: AP и SI. AP — это доля риска А и В, обусловленная супераддитивностью воздействий А и В. SI переводит статистику RERI не в разность, а в отношение.

Давайте посмотрим, как это работает

Мы проиллюстрируем работу reri на примере оценки риска врожденных пороков развития при воздействии нитратов. Мы используем смоделированный набор данных (nitrates.dta), который имитирует результаты Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Исходным показателем является трубка, представляющая дефекты нервной трубки. Воздействием являются два показателя потребления нитратов: наркотик, со значениями 0/1, указывающими на воздействие нитрозируемых наркотиков, и нитрат, также со значениями 0/1, представляющими низкое или высокое ежедневное потребление нитратов из питьевой воды.

Мы хотим построить аддитивную модель для взаимодействия лекарств и нитратов. Поскольку это обсервационное исследование, для него подходит биномиальная модель риска, которую мы построили с помощью программы binreg:

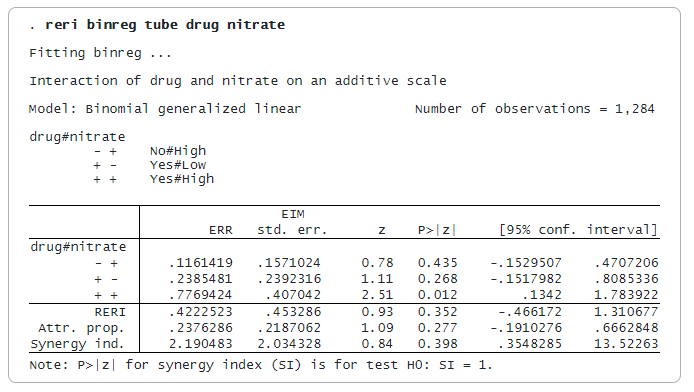
Взаимодействия, созданные reri, представляют собой разобщенные группы в данных. Взаимодействие «-+» соответствует значениям «лекарство» = «нет» b «нитрат» = «высокий«. Аналогично определяются взаимодействия +- и ++, как показано в легенде. Взаимодействие — является контрольной категорией.

Оценки рядом с -+, +- и ++ являются показателями избыточного относительного риска (ERR), определяемого как RR минус один. ERR больше 0 означает, что RR больше 1.

Если модель аддитивная, то мы имеем

  ERR(++) = ERR(-+) + ERR(+-)

Статистика RERI представляет собой разность между двумя сторонами этого уравнения:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Оценка ERR(++) равна 0,777, что больше ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Таким образом, модель является супераддитивной. Статистика RERI равна 0,422 — разница между 0,777 и 0,355.

Статистика AP — это доля риска для взаимодействия ++, которая обусловлена риском, превышающим аддитивный. В нашем примере оценка AP равна 0,24. Статистика SI — это избыточный риск, выраженный в виде отношения, а не разности. Ее оценка 2,19 больше 1, что предполагает положительное взаимодействие или супераддитивность.

Помимо моделей binreg, reri может использовать логистические, пуассоновские, nbreg, stcox, stintcox, streg и stintreg модели.

Ссылки

Андерссон Т., Альфредссон Л., Каллберг Х., Здравкович С. и Ольбом А. 2005. Расчет мер биологического взаимодействия. European Journal of Epidemiology 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Пренатальное потребление нитратов из питьевой воды и отдельные врожденные пороки развития у потомства участников Национального исследования по профилактике врожденных пороков развития. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland, and T. L. Lash. 2008. Modern Epidemiology. 3rd ed. Philadelphia: Lippincott Williams & Wilkins.