Áttekintés

Az új reri parancs additív kölcsönhatásokat becsül binomiális általános lineáris modellekben; logisztikus, Poisson és negatív binomiális regressziókban; valamint Cox és más túlélési modellekben.

Az RR-t becslő modellekben a kétirányú kölcsönhatásokat általában multiplikatív kölcsönhatásokként fejezik ki. Számos biológiai folyamat esetében azonban a kölcsönhatás additív modellje jobban modellezheti a folyamatot, mint a multiplikatív modell (lásd például Andersson et al. [2005]).

Az A és B bináris expozíciók esetében gyakran szeretnénk modellezni a pozitív kimenetel kockázatát az A és B expozíciót egyaránt átélő alanyok esetében, összehasonlítva a csak A-t és a csak B-t átélő alanyokkal, vagyis az A és B kölcsönhatását szeretnénk vizsgálni.

A multiplikatív modellben az A és B alanyok kockázata feltételezhetően egyenlő a csak A kockázatának és a csak B kockázatának szorzatával. Ha az A és B kockázata megegyezik a multiplikatív kockázattal, akkor azt mondjuk, hogy nincs A és B kölcsönhatása, ha a kockázat nagyobb, mint a multiplikatív kockázat, akkor azt mondjuk, hogy pozitív kölcsönhatás van. A multiplikatív modellek azért kényelmesek, mert egyszerűen megadhatók, és könnyű tesztelni, hogy a kölcsönhatás nagyobb (vagy kisebb)-e a multiplikatívnál.

Additív modellben az A és B alanyok kockázata feltételezhetően egyenlő a csak A kockázata plusz a csak B kockázata. Ennél a hipotézisnél azt szeretnénk megvizsgálni, hogy az A és B kockázata mennyivel nagyobb (vagy kisebb), mint az additív kockázat.

A RERI-statisztika ez a kockázati különbség, RR-ek segítségével megfogalmazva (Rothman, Greenland és Lash 2008). A 0 értékű RERI-statisztika azt jelenti, hogy a kockázat additív. A pozitív RERI-statisztika azt jelenti, hogy a kockázat szuperadditív, a negatív RERI-statisztika pedig azt, hogy a kockázat szubadditív. A RERI-statisztika statisztikai szignifikancia tesztje egyszerű, de nem olyan egyszerű, mint a multiplikatív modell tesztje.

A RERI statisztikán kívül a reri parancs két másik kapcsolódó statisztikát is közöl: AP és SI. Az AP az A és B kockázatának az A és B expozíciók szuperadditivitása miatti aránya. Az SI a RERI-statisztikát nem különbségként, hanem arányként állítja újra.

Lássuk, hogyan működik

A reri-t egy olyan példával illusztráljuk, amely a születési rendellenességek kockázatát becsüli meg a nitrátoknak való kitettség miatt. Egy szimulált adatállományt (nitrates.dta) használunk, amely a Brender et al. (2013) eredményeit utánozza.

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

A mi kimeneti mérőszámunk a cső, amely az idegcsődefektusokat jelöli. Az expozíciók a nitrátbevitel két mérőszáma: gyógyszer, 0/1 értékkel, ami a nitrozálható gyógyszer-expozíciót jelzi; és nitrát, szintén 0/1 értékkel, ami az ivóvízből származó nitrátok alacsony vagy magas napi fogyasztását jelenti.

A gyógyszer és a nitrát kölcsönhatására egy additív modellt szeretnénk illeszteni. Mivel ez egy megfigyelési vizsgálat, a kockázat binomiális modellje megfelelő, és ezt a binreg segítségével illesztjük be:

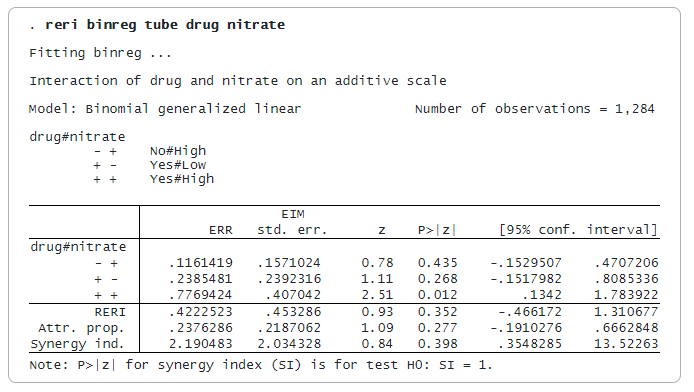
A reri által létrehozott kölcsönhatások diszjunkt csoportokat képviselnek az adatokban. A -+ kölcsönhatás a drog = Nem és a nitrát = Magas. A +- és ++ kölcsönhatások hasonlóan vannak definiálva, ahogy a legendában látható. A — interakció a referencia-kategória.

A -+, +- és ++ mellett szereplő becslések a relatív többletkockázat (ERR) mértékét jelentik, amelyet RR mínusz egyként definiálnak. A 0-nál nagyobb ERR azt jelenti, hogy az RR nagyobb, mint 1.

Ha a modell additív, akkor a következőket kapnánk

  ERR(++) = ERR(-+) + ERR(+-)

A RERI-statisztika az egyenlet két oldala közötti különbség:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Az ERR(++) becsült értéke 0,777, ami nagyobb, mint az ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355 érték. A modell tehát szuperadditív. A RERI-statisztika 0,422, ami a 0,777 és a 0,355 közötti különbség.

Az AP statisztika a ++ kölcsönhatás kockázatának azon aránya, amely az additivitáson felüli kockázatnak köszönhető. Példánkban az AP becslése 0,24. Az SI-statisztika a többletkockázat, amelyet nem különbségként, hanem arányként fejezünk ki. A 2,19-es becslése nagyobb, mint 1, ami pozitív kölcsönhatást vagy szuperadditivitást jelent.

A binreg modellek mellett a reri képes logisztikus, poisson, nbreg, stcox, stintcox, streg és stintreg modellek illesztésére is.

Hivatkozások

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic és A. Ahlbom. 2005. A biológiai kölcsönhatás mérőszámainak kiszámítása. European Journal of Epidemiology 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Prenatális nitrátbevitel az ivóvízből és kiválasztott születési rendellenességek a National Birth Defects Prevention Study résztvevőinek utódainál. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland és T. L. Lash. 2008. Modern epidemiológia. 3. kiadás. Philadelphia: Lippincott Williams & Wilkins.