L’EM traditionnelle traite de données binaires ou continues à deux échantillons où le résultat d’intérêt est mesuré dans deux groupes généralement désignés comme le groupe de traitement et le groupe de contrôle. Par exemple, une EM peut comparer le risque de contracter une maladie (résultat binaire) entre deux groupes : les vaccinés et les non vaccinés. Ou peut-être voulons-nous comparer la perte de poids (résultat continu) entre deux groupes de sujets qui ont suivi des régimes différents, par exemple le régime céto ou le jeûne intermittent.

Cette situation à deux groupes n’est cependant pas toujours présente dans une AMM. Par exemple, les Nations unies peuvent réaliser une EM pour évaluer la prévalence d’une certaine maladie dans les pays afin d’allouer les ressources appropriées pour la combattre. Ou encore, le ministère de l’éducation réalise une EM pour évaluer la proportion d’élèves qui abandonnent l’école secondaire et utilise ses résultats pour orienter le budget de l’éducation de la maternelle à la 12e année. Dans les deux exemples, nous disposons de données binaires à un échantillon, dans lesquelles les sujets appartiennent à un seul groupe et où l’intérêt réside dans la proportion d’individus ayant vécu un certain événement (contracter la maladie dans le premier exemple et abandonner l’école secondaire dans le second). Dans ce contexte, les tailles d’effet telles que les proportions transformées par Freeman-Tukey ou les proportions transformées par logit sont généralement utilisées dans l’EM.

Voyons comment cela fonctionne

-> Exemple de données : Proportions de végétariens dans les sept régions des États-Unis.
-> Méta-analyse de données binaires à un échantillon

Exemple de données : Proportions de végétariens dans les sept régions des États-Unis.

Rencontrer ses futurs beaux-parents pour la première fois peut être éprouvant. Vous avez décidé d’impressionner votre future belle-mère, qui a l’intention d’ouvrir un restaurant en ligne qui livre de la nourriture dans tous les États-Unis. En tant que statisticien de la famille, vous avez suggéré de réaliser une étude de marché pour évaluer la proportion globale de végétariens (et de végétaliens) dans les sept régions des États-Unis. En vous basant sur les résultats de l’étude de marché, vous espérez aider le restaurant à adapter des recettes plus respectueuses des végétariens à des régions spécifiques des États-Unis.

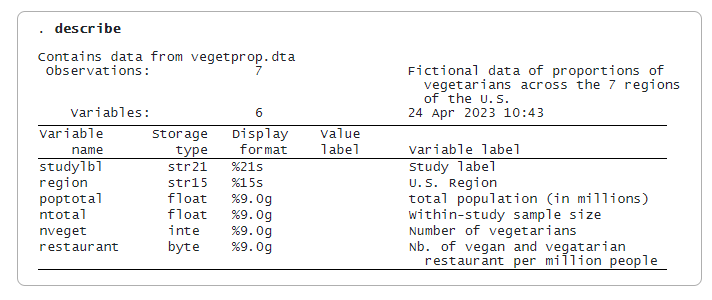
Méta-analyse de données binaires à un échantillon

Les variables nveget et ntotal représentent le nombre de végétariens et le nombre total de sujets dans chaque étude. Par défaut, meta esize calcule la proportion transformée en double arcsine de Freeman-Tukey pour chaque étude. Il s’agit d’une transformation qui stabilise la variance et qui est particulièrement préférable lorsque les proportions sont proches de 0 ou de 1.

Déclarez vos données en tant que métadonnées via meta esize

Vous pouvez spécifier la proportion transformée en logit comme taille d’effet en utilisant l’option esize(logitprop). Comme la variance de la proportion transformée en logit dépend de la proportion elle-même, l’AM de cette taille d’effet tend à attribuer des poids artificiellement faibles aux études dont les proportions sont proches de 0 ou de 1.

Il se peut que vous souhaitiez calculer les proportions non transformées ; cependant, cela n’est recommandé que si toutes les proportions rapportées par les études sont proches de 0,5, ce qui n’est pas courant dans la pratique.

. meta update, esize(proportion)
(Output omitted)

Diagrammes de forêt et autres techniques de méta-analyse

Pour poursuivre avec la première spécification de meta esize, après avoir calculé l’ampleur de l’effet qui vous intéresse et déclaré vos données en tant que meta data, vous pouvez utiliser n’importe quelle technique d’analyse de marché comme d’habitude. Par exemple, pour construire un diagramme forestier, nous tapons

. meta forest, proportion

L’option proportion spécifie que les résultats doivent être rapportés sous forme de proportions au lieu des proportions transformées par Freeman-Tukey par défaut. Cela équivaut à appliquer la transformation inverse de Freeman-Tukey en utilisant l’option transform(invftukey). La proportion globale (moyenne) de végétariens est de 0,06 avec un IC de [.04, 0,08].

Vous pouvez également présenter vos résultats sous la forme, par exemple, du nombre de végétariens pour 1 000 personnes en utilisant la sous-option scale() de l’option transform(). Nous indiquerons également la région correspondante (région variable) de chaque étude sur le diagramme forestier.

. meta forest _id _data region _plot _esci _weight,
  transform(invftukey, scale(1000)) esrefline insidemarker

Les diagrammes de forêt ci-dessus ont révélé des différences substantielles entre les proportions de végétariens, avec une prévalence plus élevée de végétariens dans les régions de la côte pacifique, de la Nouvelle-Angleterre et du centre du littoral atlantique par rapport au reste des régions des États-Unis.

La réunion avec les beaux-parents est imminente. Heureusement pour vous, grâce au graphique forestier ci-dessus, vous pouvez conseiller à votre future belle-mère d’incorporer davantage de recettes végétariennes dans son menu pour les régions susmentionnées et l’impressionner !