Vue d’ensemble

La nouvelle commande reri estime les interactions additives dans les modèles linéaires généralisés binomiaux, les régressions logistiques, de Poisson et binomiales négatives, ainsi que les modèles de survie de Cox et autres.

Les interactions bidirectionnelles dans les modèles qui estiment le RR sont généralement exprimées comme des interactions multiplicatives. Cependant, pour de nombreux processus biologiques, un modèle additif pour l’interaction peut mieux modéliser le processus qu’un modèle multiplicatif (voir, par exemple, Andersson et al. [2005]).

Pour les expositions binaires A et B, nous voulons souvent modéliser le risque d’un résultat positif pour les sujets ayant à la fois A et B par rapport aux sujets n’ayant que A et à ceux n’ayant que B. En d’autres termes, nous voulons examiner l’interaction de A et B.

Dans un modèle multiplicatif, le risque pour les sujets présentant A et B est supposé être égal au risque pour A seul multiplié par le risque pour B seul. Si le risque pour A et B est égal au risque multiplicatif, nous disons qu’il n’y a pas d’interaction entre A et B. Si le risque est supérieur au risque multiplicatif, nous disons qu’il y a une interaction positive. Les modèles multiplicatifs sont pratiques car ils sont simples à spécifier et il est facile de vérifier si l’interaction est supérieure (ou inférieure) au risque multiplicatif.

Dans un modèle additif, le risque pour les sujets présentant A et B est supposé être égal au risque pour A seul plus le risque pour B seul. Pour cette hypothèse, nous voulons examiner dans quelle mesure le risque pour A et B est supérieur (ou inférieur) au risque additif.

La statistique RERI est cette différence de risque formulée à l’aide des RR (Rothman, Greenland et Lash 2008). Une statistique RERI de 0 signifie que le risque est additif. Une statistique RERI positive signifie que le risque est superadditif, et une statistique RERI négative signifie que le risque est sous-additif. Le test de signification statistique de la statistique RERI est simple, mais il n’est pas aussi simple que le test pour le modèle multiplicatif.

Outre la statistique RERI, la commande reri fournit deux autres statistiques connexes : AP et SI. AP est la proportion du risque de A et B due à la superadditivité des expositions A et B. SI reformule la statistique RERI sous la forme d’un ratio plutôt que d’une différence.

Voyons comment cela fonctionne

Nous illustrons reri avec un exemple qui estime le risque de malformations congénitales dues à l’exposition aux nitrates. Nous utilisons un jeu de données simulé (nitrates.dta) qui reproduit les résultats de Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Notre mesure de résultat est le tube, représentant les anomalies du tube neural. Les expositions sont deux mesures de la consommation de nitrates : le médicament, avec des valeurs 0/1, indiquant l’exposition aux médicaments nitrosables, et le nitrate, également avec des valeurs 0/1, représentant une consommation quotidienne faible ou élevée de nitrates dans l’eau de boisson.

Nous voulons ajuster un modèle additif pour l’interaction entre le médicament et le nitrate. Comme il s’agit d’une étude observationnelle, un modèle binomial de risque est approprié, et nous l’ajustons en utilisant binreg :

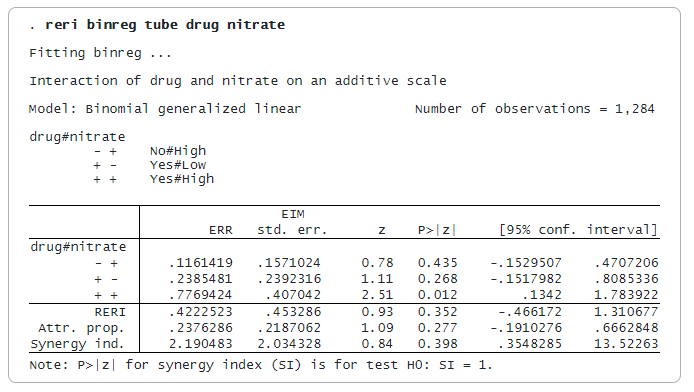
Les interactions créées par reri représentent des groupes disjoints dans les données. L’interaction -+ correspond à médicament = non et nitrate = élevé. Les interactions +- et ++ sont définies de la même manière, comme indiqué dans la légende. L’interaction — est la catégorie de référence.

Les estimations en regard de -+, +- et ++ sont des mesures de l’excès de risque relatif (ERR), défini comme le RR moins un. Un ERR supérieur à 0 signifie que le RR est supérieur à 1.

Si le modèle est additif, nous aurions

  ERR(++) = ERR(-+) + ERR(+-)

La statistique RERI est la différence entre les deux côtés de cette équation :

  RERI = ERR(++) - ERR(-+) - ERR(+-)

L’estimation de ERR(++) est de 0,777, ce qui est supérieur à ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Le modèle est donc superadditif. La statistique RERI est de 0,422, soit la différence entre 0,777 et 0,355.

La statistique AP est la proportion du risque pour l’interaction ++ qui est due au risque superadditif. Dans notre exemple, l’estimation de la statistique AP est de 0,24. La statistique SI est l’excès de risque exprimé sous la forme d’un ratio plutôt que d’une différence. Son estimation de 2,19 est supérieure à 1, ce qui implique une interaction positive ou une superadditivité.

Outre les modèles binreg, reri peut ajuster des modèles logistiques, de poisson, nbreg, stcox, stintcox, streg et stintreg.

Références

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic, et A. Ahlbom. 2005. Calculating measures of biological interaction. European Journal of Epidemiology 20 : 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Prenatal nitrate intake from drinking water and selected birth defects in offspring of participants in the National Birth Defects Prevention Study. Environmental Health Perspectives 121 : 1083-1089.

Rothman, K. J., S. Greenland, et T. L. Lash. 2008. Modern Epidemiology. 3e éd. Philadelphie : Lippincott Williams & Wilkins.