Übersicht

Der neue Befehl reri schätzt additive Interaktionen in binomialen verallgemeinerten linearen Modellen, logistischen, Poisson- und negativen binomialen Regressionen sowie Cox- und anderen Überlebensmodellen.

Zwei-Wege-Interaktionen in Modellen, die RR schätzen, werden normalerweise als multiplikative Interaktionen ausgedrückt. Bei vielen biologischen Prozessen kann jedoch ein additives Modell für die Wechselwirkung den Prozess besser modellieren als ein multiplikatives Modell (siehe z. B. Andersson et al. [2005]).

Bei binären Expositionen A und B möchten wir häufig das Risiko eines positiven Ergebnisses für Probanden modellieren, die sowohl A als auch B haben, im Vergleich zu Probanden, die nur A haben, und solchen, die nur B haben, d. h. wir möchten die Interaktion von A und B untersuchen.

In einem multiplikativen Modell wird angenommen, dass das Risiko für Personen mit A und B gleich dem Risiko für nur A mal dem Risiko für nur B ist. Wenn das Risiko für A und B gleich dem multiplikativen Risiko ist, sagen wir, dass es keine Interaktion von A und B gibt. Multiplikative Modelle sind praktisch, weil sie einfach zu spezifizieren sind und es leicht zu testen ist, ob die Wechselwirkung größer (oder kleiner) als multiplikativ ist.

Bei einem additiven Modell wird angenommen, dass das Risiko für Personen mit A und B gleich dem Risiko für nur A plus dem Risiko für nur B ist. Für diese Hypothese wollen wir untersuchen, wie viel das Risiko für A und B größer (oder kleiner) ist als das additive Risiko.

Die RERI-Statistik ist diese Risikodifferenz, die unter Verwendung von RRs formuliert wird (Rothman, Greenland und Lash 2008). Eine RERI-Statistik von 0 bedeutet, dass das Risiko additiv ist. Eine positive RERI-Statistik bedeutet, dass das Risiko superadditiv ist, und eine negative RERI-Statistik bedeutet, dass das Risiko subadditiv ist. Der Test der statistischen Signifikanz der RERI-Statistik ist einfach, aber nicht so einfach wie der Test für das multiplikative Modell.

Neben der RERI-Statistik gibt der Befehl reri zwei weitere verwandte Statistiken aus: AP und SI. AP ist der Anteil des Risikos von A und B aufgrund der Superadditivität der Expositionen A und B. SI stellt die RERI-Statistik als Verhältnis und nicht als Differenz dar.

Wir wollen sehen, wie es funktioniert

Wir veranschaulichen reri anhand eines Beispiels, das das Risiko von Geburtsfehlern durch Nitratexposition schätzt. Wir verwenden einen simulierten Datensatz (nitrates.dta), der die Ergebnisse von Brender et al. (2013) nachahmt.

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Unser Ergebnismaß ist „tube„, das für Neuralrohrdefekte steht. Bei den Expositionen handelt es sich um zwei Maße für die Nitrataufnahme: Droge mit den Werten 0/1, was die Exposition gegenüber nitrosierbaren Drogen angibt, und Nitrat, ebenfalls mit den Werten 0/1, was entweder einen niedrigen oder hohen täglichen Konsum von Nitraten aus dem Trinkwasser angibt.

Wir wollen ein additives Modell für die Interaktion von Droge und Nitrat erstellen. Da es sich um eine Beobachtungsstudie handelt, ist ein binomiales Risikomodell angemessen, das wir mit binreg anpassen:

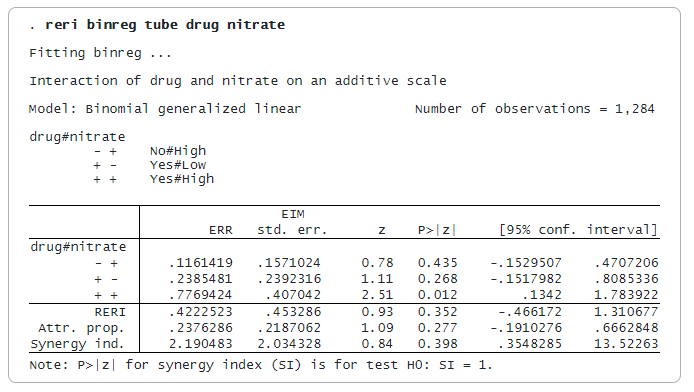
Die von reri erstellten Interaktionen stellen disjunkte Gruppen in den Daten dar. Die Interaktion -+ steht für Droge = Nein und Nitrat = Hoch. Die Interaktionen +- und ++ sind ähnlich definiert, wie in der Legende dargestellt. Die Interaktion — ist die Referenzkategorie.

Die Schätzungen neben -+, +- und ++ sind Maße für das überschüssige relative Risiko (ERR), definiert als RR minus eins. ERR größer als 0 bedeutet, dass das RR größer als 1 ist.

Wenn das Modell additiv ist, würde dies bedeuten

  ERR(++) = ERR(-+) + ERR(+-)

Die RERI-Statistik ist die Differenz zwischen den beiden Seiten dieser Gleichung:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Die Schätzung der ERR(++) beträgt 0,777, was größer ist als ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Das Modell ist also superadditiv. Die RERI-Statistik beträgt 0,422, also die Differenz zwischen 0,777 und 0,355.

Die AP-Statistik ist der Anteil des Risikos für die ++ Interaktion, der auf das Risiko zurückzuführen ist, das über dem additiven liegt. In unserem Beispiel beträgt der Schätzwert für AP 0,24. Die SI-Statistik ist das Überschussrisiko, ausgedrückt als Verhältnis und nicht als Differenz. Ihr Schätzwert von 2,19 ist größer als 1, was auf eine positive Interaktion oder Superadditivität schließen lässt.

Neben binreg-Modellen kann reri auch logistische, Poisson-, nbreg-, stcox-, stintcox-, streg- und stintreg-Modelle anpassen.

Referenzen

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic, und A. Ahlbom. 2005. Berechnung von Maßen der biologischen Interaktion. Europäische Zeitschrift für Epidemiologie 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Pränatale Nitrataufnahme aus dem Trinkwasser und ausgewählte Geburtsfehler bei Nachkommen von Teilnehmern der National Birth Defects Prevention Study. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland, und T. L. Lash. 2008. Moderne Epidemiologie. 3. Auflage. Philadelphia: Lippincott Williams & Wilkins.