Neu in 
Multinomiales Logit-Modell für Paneldaten
Das multinomiale Logit-Modell (MNL) ist eine beliebte Methode zur Modellierung kategorialer Ergebnisse, die keine natürliche Reihenfolge aufweisen – wie z. B. Beruf, politische Partei oder Restaurantwahl.
In Längsschnitt-/Paneldaten beobachten wir eine Abfolge von Ergebnissen über die Zeit. Nehmen wir an, wir beobachten jede Woche die Restaurantwahl von Einzelpersonen. Glauben Sie, dass die Restaurantwahlen von Woche zu Woche unabhängig sind? Wahrscheinlich nicht. Jemand, der italienisches Essen mag, wird wahrscheinlich mehrmals ein italienisches Restaurant wählen. Diese Entscheidungen werden durch zugrundeliegende persönliche Vorlieben und Eigenschaften bestimmt, von denen einige nicht beobachtet werden.
Der neue Stata-Befehl xtmlogit passt MNL-Modelle mit zufälligen Effekten und bedingten festen Effekten für kategoriale Ergebnisse an, die über die Zeit beobachtet werden.
Um ein multinomiales Logit-Modell mit zufälligen Effekten anzupassen, können wir Folgendes eingeben
. xtset subject . xtmlogit restaurant age
und schätzen Sie die standardmäßigen multinomialen Logit-Koeffizienten, die zeitinvariante subjektspezifische Merkmale berücksichtigen, indem Sie für jede Ergebnisebene spezifische Zufallseffekte einbeziehen.
Mit dem obigen Befehl wird angenommen, dass die zufälligen Effekte normalverteilt und unabhängig über die Ergebnisebenen (Restaurantwahlen) sind, aber es werden mehrere Varianz-Kovarianz-Strukturen unterstützt, einschließlich einer völlig unbeschränkten Kovarianz:
. xtmlogit restaurant age, covariance(unstructured)
Wenn Sie vermuten, dass subjektspezifische Effekte mit dem Alter korreliert sein könnten, können Sie einen Schätzer mit bedingten festen Effekten verwenden, um dies zu berücksichtigen:
. xtmlogit restaurant age, fe
Höhepunkte
Paneldatenmodellierung von ungeordneten kategorialen Outcomes
Schätzer mit zufälligen Effekten
- Wahl der Kovarianzstruktur für zufällige Effekte
- Unabhängig
- Identität
- Geteilt
- Austauschbar
- Unstrukturiert
Bedingter Schätzer mit festen Effekten (FE)
- Permutationsuntermengen verringern den Fluch der Dimensionalität
Bayessche Schätzung
Robuste, clusterrobuste und Bootstrap-Standardfehler
Unterstützung für komplexe Vermessungsdaten
Zeigen Sie, wie es funktioniert
Wir möchten herausfinden, ob Individuen mit höherer Wahrscheinlichkeit nicht erwerbstätig sind, wenn sie Kinder unter fünf Jahren in ihrem Haushalt haben. Wir werden einen (fiktiven) Datensatz von Männern und Frauen verwenden, die alle zwei Jahre zu ihrem Beschäftigungsstatus befragt wurden.
. use https://www.stata-press.com/data/r17/estatus (Fictitious employment status data)
Hier ist ein Auszug aus dem Datensatz, der den Beschäftigungsverlauf für drei Personen zeigt:
. list id year estatus hhchild age in 22/41, sepby(id) noobs
| id year estatus hhchild age | ||
| 5 2002 Employed Yes 38 | ||
| 5 2004 Employed No 40 | ||
| 5 2006 Employed No 42 | ||
| 5 2008 Employed No 44 | ||
| 5 2010 Out of labor force No 46 | ||
| 5 2012 Out of labor force No 48 | ||
| 5 2014 Unemployed No 50 | ||
| 6 2002 Unemployed Yes 31 | ||
| 6 2004 Employed Yes 33 | ||
| 6 2006 Out of labor force Yes 35 | ||
| 6 2008 Unemployed Yes 37 | ||
| 6 2010 Out of labor force Yes 39 | ||
| 6 2012 Unemployed No 41 | ||
| 7 2002 Out of labor force Yes 33 | ||
| 7 2004 Employed Yes 35 | ||
| 7 2006 Employed Yes 37 | ||
| 7 2008 Out of labor force Yes 39 | ||
| 7 2010 Employed No 41 | ||
| 7 2012 Employed No 43 | ||
| 7 2014 Employed No 45 | ||
Das Ergebnis von Interesse ist der Beschäftigungsstatus (estatus), der drei Stufen hat: Beschäftigt, arbeitslos (aber arbeitssuchend) und nicht erwerbstätig (nicht arbeitssuchend). Unser interessanter Prädiktor, hhchild, gibt an, ob sie zum Zeitpunkt der Befragung Kinder unter fünf Jahren in ihrem Haushalt haben.
Bevor wir unser Modell anpassen können, müssen wir unsere Panel-Identifizierungsvariable, id, mithilfe von xtset festlegen.
. xtset id Panel variable: id (unbalanced)
Nun können wir xtmlogit verwenden, um die Wahrscheinlichkeit jeder Beschäftigungsart durch hhchild zu modellieren, während wir für die Effekte des Alters, des jährlichen Haushaltseinkommens (hhincome) und der Tatsache, ob eine signifikante andere Person ebenfalls im Haushalt lebte (hhsigno), kontrollieren. Wir beginnen mit einem Modell mit zufälligen Effekten (die Vorgabe) und verwenden die Option rrr, um potenzierte Koeffizienten zu erhalten, die als relative Risikoverhältnisse interpretiert werden können.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, rrr
Fitting comparison model ...
Refining starting values:
Grid node 0: log likelihood = -4504.5591
Grid node 1: log likelihood = -4538.6352
Fitting full model:
Iteration 0: log likelihood = -4504.5591
Iteration 1: log likelihood = -4495.871
Iteration 2: log likelihood = -4490.5098
Iteration 3: log likelihood = -4490.4197
Iteration 4: log likelihood = -4490.4196
Random-effects multinomial logistic regression Number of obs = 4,761
Group variable: id Number of groups = 800
Random effects u_i ~ Gaussian Obs per group:
min = 5
avg = 6.0
max = 7
Integration method: mvaghermite Integration pts. = 7
Wald chi2(8) = 199.25
Log likelihood = -4490.4196 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.579937 .1513905 4.77 0.000 1.309414 1.906349 | |||||
| age | .9947946 .0065832 -0.79 0.430 .981975 1.007781 | |||||
| hhincome | .9954927 .0018251 -2.46 0.014 .9919221 .9990762 | |||||
| hhsigno | ||||||
| Yes | 1.642859 .1550291 5.26 0.000 1.365452 1.976625 | |||||
| _cons | .4949307 .1392991 -2.50 0.012 .2850836 .859244 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | .9607243 .1148148 -0.34 0.737 .7601038 1.214296 | |||||
| age | 1.004257 .008211 0.52 0.603 .9882918 1.02048 | |||||
| hhincome | .9696874 .0025722 -11.60 0.000 .964659 .9747421 | |||||
| hhsigno | ||||||
| Yes | 1.099323 .1310654 0.79 0.427 .8702452 1.388701 | |||||
| _cons | .8078165 .280628 -0.61 0.539 .4088963 1.595924 | |||||
| Employed | (base outcome) | |||||
| var(u1) | .8573133 .1083915 .6691459 1.098394 | |||||
| var(u2) | .7378532 .1388652 .5102376 1.067008 | |||||
Die ersten beiden Abschnitte der Ausgabe zeigen die Schätzungen des relativen Risikoverhältnisses unserer Prädiktoren in Bezug auf die Basiskategorie Beschäftigt. Der letzte Abschnitt zeigt die geschätzten Varianzen der zufälligen Effekte. Standardmäßig sind die zufälligen Effekte unkorreliert, aber ihre Kovarianzstruktur kann mit der Option covariance() geändert werden. Zum Beispiel können Korrelationen zwischen zufälligen Effekten mit covariance(unstructured) geschätzt werden, oder jede Kategorie kann sich einen gemeinsamen zufälligen Effekt mit covariance(shared) teilen.
Unter Berücksichtigung des Alters, des Haushaltseinkommens und des Vorhandenseins einer signifikanten anderen Person im Haushalt ist das relative Risiko, nicht erwerbstätig zu sein, für Personen, die mindestens ein Kind unter 5 Jahren im Haushalt haben, im Vergleich zu Personen, die keine Kinder unter 5 Jahren im Haushalt haben, 1,6 Mal so groß wie das relative Risiko, erwerbstätig zu sein (95% CI [1,3, 1,9]). Um diese Effekte in Form von Wahrscheinlichkeiten zu verstehen, können wir den Befehl margins verwenden.
. margins hhchild Predictive margins Number of obs = 4,761 Model VCE: OIM 1._predict: Pr(estatus==Out_of_labor_force), predict(pr outcome(1)) 2._predict: Pr(estatus==Unemployed), predict(pr outcome(2)) 3._predict: Pr(estatus==Employed), predict(pr outcome(3))
| Delta-method | ||||||
| Margin std. err. z P>|z| [95% conf. interval] | ||||||
| _predict#hhchild | ||||||
| 1#No | .3025675 .0131546 23.00 0.000 .276785 .32835 | |||||
| 1#Yes | .3912476 .0120405 32.49 0.000 .3676486 .4148466 | |||||
| 2#No | .1628713 .0101131 16.11 0.000 .1430501 .1826925 | |||||
| 2#Yes | .1398537 .0079462 17.60 0.000 .1242794 .1554279 | |||||
| 3#No | .5345612 .0136994 39.02 0.000 .5077108 .5614116 | |||||
| 3#Yes | .4688987 .0116594 40.22 0.000 .4460468 .4917507 | |||||
Für eine Person ohne Kinder beträgt die erwartete Wahrscheinlichkeit, nicht erwerbstätig zu sein (mit 1#Nein) 0,30, die erwartete Wahrscheinlichkeit, arbeitslos zu sein (2#Nein) 0,16 und die erwartete Wahrscheinlichkeit, erwerbstätig zu sein, 0,53 (3#Nein). Wir finden auch, dass Personen mit Kindern im Haushalt ihre Wahrscheinlichkeit, nicht erwerbstätig zu sein, um 9 Prozentpunkte erhöhen. Wir können sehen, wie sich diese Wahrscheinlichkeiten in Abhängigkeit vom Haushaltseinkommen ändern, indem wir einen zusätzlichen margins-Befehl verwenden und die Ergebnisse mit marginsplot visualisieren.
. quietly margins hhchild, at(hhincome=(20(20)100))
. marginsplot, by(_predict, label("Out of labor force" "Unemployed" "Employed"))
byopts(rows(1) title("Marginal probabilities of employment status"))
legend(order(4 "Child under 5 at home" 3 "No child under 5 at home"))
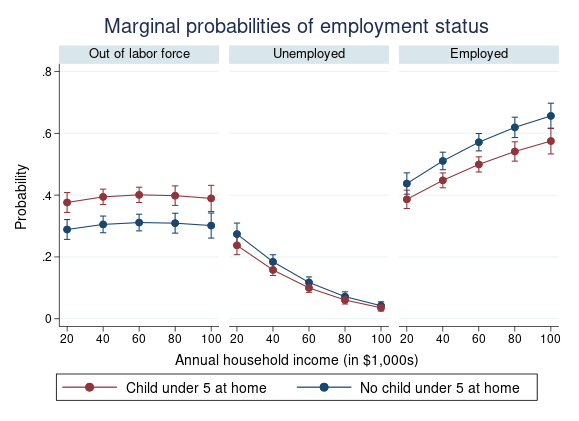
Um separate Diagramme für jedes Ergebnis zu erhalten, haben wir die Option by(_predict) in marginsplot verwendet. Die übrigen Optionen fügen Titel und Beschriftungen hinzu.
Vergleicht man die Linien innerhalb jeder Beschäftigungskategorie, so sieht man, dass ein Kind zu Hause keinen großen Einfluss auf die Wahrscheinlichkeit hat, arbeitslos zu sein, aber die Entscheidung, zu arbeiten oder nicht erwerbstätig zu sein, beeinflusst.
In dem Modell, das wir gerade angepasst haben, haben wir Zufallseffekte verwendet, um unbeobachtete Merkmale der Individuen in unserem Datensatz zu berücksichtigen. Modelle mit zufälligen Effekten erfordern, dass die zufälligen Effekte unkorreliert mit den Prädiktoren sind, und das MNL-Modell mit zufälligen Effekten ist keine Ausnahme. Eine weit verbreitete Alternative ist der Schätzer mit festen Effekten. Um unser Modell mit bedingten festen Effekten anzupassen, fügen wir einfach die Option fe hinzu.
. xtmlogit estatus i.hhchild age hhincome i.hhsigno, fe rrr
note: 80 groups (451 obs) omitted because of no variation in the outcome variable over time.
Computing initial values ...
Setting up 26,168 permutations:
....10%....20%....30%....40%....50%....60%....70%....80%....90%....100%
Fitting full model:
Iteration 0: log likelihood = -2154.4175
Iteration 1: log likelihood = -2154.2058
Iteration 2: log likelihood = -2154.2057
Fixed-effects multinomial logistic regression Number of obs = 4,310
Group variable: id Number of groups = 720
Obs per group:
min = 5
avg = 6.0
max = 7
LR chi2(8) = 67.42
Log likelihood = -2154.2057 Prob > chi2 = 0.0000
| estatus | RRR Std. err. z P>|z| [95% conf. interval] | |||||
| Out_of_labor_force | ||||||
| hhchild | ||||||
| Yes | 1.784236 .2237128 4.62 0.000 1.395488 2.28128 | |||||
| age | .9977834 .0146507 -0.15 0.880 .9694778 1.026915 | |||||
| hhincome | .9895225 .0086923 -1.20 0.231 .9726318 1.006707 | |||||
| hhsigno | ||||||
| Yes | 1.658753 .1654425 5.07 0.000 1.364217 2.016878 | |||||
| Unemployed | ||||||
| hhchild | ||||||
| Yes | 1.181866 .1933766 1.02 0.307 .8576197 1.628702 | |||||
| age | 1.004991 .0194887 0.26 0.797 .967511 1.043924 | |||||
| hhincome | .9717411 .0116616 -2.39 0.017 .9491514 .9948684 | |||||
| hhsigno | ||||||
| Yes | 1.11936 .1454154 0.87 0.385 .8677426 1.443939 | |||||
| Employed | (base outcome) | |||||
Die Ergebnisse sind ähnlich wie die des Random-Effects-Schätzers. Und sie können auf die gleiche Weise interpretiert werden.
