Преглед

Новата команда reri оценява адитивните взаимодействия в биномни обобщени линейни модели; логистична, Поасонова и отрицателна биномна регресия; както и модели на Кокс и други модели на оцеляване.

Двупосочните взаимодействия в моделите, които оценяват RR, обикновено се изразяват като мултипликативни взаимодействия. За много биологични процеси обаче адитивният модел за взаимодействието може да моделира процеса по-добре от мултипликативния (вж. например Andersson et al. [2005]).

За бинарни експозиции А и В често искаме да моделираме риска от положителен резултат за субектите, които имат и А, и В, в сравнение със субектите, които имат само А, и тези, които имат само В. Тоест искаме да изследваме взаимодействието на А и В.

В мултипликативния модел се предполага, че рискът за субекти с А и В е равен на риска само за А, умножен по риска само за В. Ако рискът за А и В е равен на мултипликативния риск, казваме, че няма взаимодействие на А и В. Ако рискът е по-голям от мултипликативния риск, казваме, че има положително взаимодействие. Мултипликативните модели са удобни, защото са лесни за определяне и е лесно да се провери дали взаимодействието е по-голямо (или по-малко) от мултипликативното.

При адитивния модел се предполага, че рискът за субектите с А и В е равен на риска само за А плюс риска само за В. За тази хипотеза искаме да проверим с колко рискът за А и В е по-голям (или по-малък) от адитивния риск.

Статистиката RERI е тази разлика в риска, формулирана с помощта на RRs (Rothman, Greenland, and Lash 2008). Статистика RERI, равна на 0, означава, че рискът е адитивен. Положителна RERI статистика означава, че рискът е суперадитивен, а отрицателна RERI статистика означава, че рискът е субадитивен. Проверката на статистическата значимост на статистиката RERI е проста, но не е толкова проста, колкото проверката за мултипликативния модел.

Освен статистиката RERI, командата reri отчита още две свързани статистики: AP и SI. AP е делът на риска на A и B, дължащ се на суперадаптивността на експозициите A и B. SI преработва статистиката RERI като съотношение, а не като разлика.

Нека видим как работи

Илюстрираме reri с пример, който оценява риска от вродени дефекти при излагане на нитрати. Използваме симулиран набор от данни (nitrates.dta), който имитира резултатите от Brender et al. (2013).

. webuse nitrates
(Simulated prenatal nitrate intake and birth defects data)

Нашият показател за резултат е тръба, представляваща дефект на невралната тръба. Експозициите са две мерки за прием на нитрати: наркотици, със стойности 0/1, показващи експозиция на нитрозиращи наркотици, и нитрати, също със стойности 0/1, показващи ниска или висока дневна консумация на нитрати от питейната вода.

Искаме да приложим адитивен модел за взаимодействието на лекарството и нитратите. Тъй като това е наблюдение, биномният модел на риска е подходящ и ние го въвеждаме с помощта на binreg:

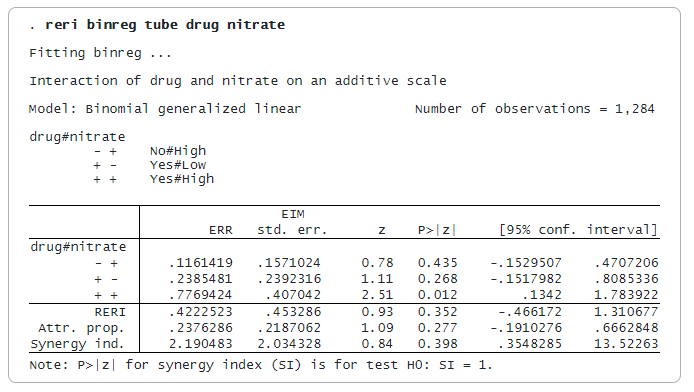
Взаимодействията, създадени от reri, представляват разделени групи в данните. Взаимодействието -+ е за лекарство = Не и нитрат = Високо. Взаимодействията +- и ++ се определят по подобен начин, както е показано в легендата. Взаимодействието – е референтната категория.

Оценките до -+, +- и ++ са мерки за свръхрелативен риск (ERR), определен като RR минус едно. ERR, по-голям от 0, означава, че RR е по-голям от 1.

Ако моделът е адитивен, ще имаме

  ERR(++) = ERR(-+) + ERR(+-)

Статистиката RERI е разликата между двете страни на това уравнение:

  RERI = ERR(++) - ERR(-+) - ERR(+-)

Оценката на ERR(++) е 0,777, което е повече от ERR(-+) + ERR(+-) = 0,116 + 0,239 = 0,355. Така че моделът е суперадитивен. Статистиката RERI е 0,422, разликата между 0,777 и 0,355.

Статистиката AP е делът на риска за взаимодействието ++, който се дължи на риска, който е над адитивен. В нашия пример оценката на AP е 0,24. Статистиката SI е свръхрискът, изразен като съотношение, а не като разлика. Нейната оценка от 2,19 е по-голяма от 1, което предполага положително взаимодействие или свръхадаптивност.

Освен binreg моделите, reri може да подбира логистични, poisson, nbreg, stcox, stintcox, streg и stintreg модели.

Препратки

Andersson, T., L. Alfredsson, H. Källberg, S. Zdravkovic и A. Ahlbom. 2005. Изчисляване на мерки за биологично взаимодействие. European Journal of Epidemiology 20: 575-579.

Brender, J. D., P. J. Weyer, P. A. Romitti, B. P. Mohanty, M. U. Shinde, A. M. Vuong, J. R. Sharkey, et al. 2013. Пренатален прием на нитрати от питейна вода и избрани вродени дефекти при потомството на участниците в Националното проучване за превенция на вродени дефекти. Environmental Health Perspectives 121: 1083-1089.

Rothman, K. J., S. Greenland, and T. L. Lash. 2008. Modern Epidemiology. 3rd ed. Philadelphia: Lippincott Williams & Wilkins.