Új a  -ben
-ben
BIC a lasso büntetés kiválasztásához
A büntetési paraméter kiválasztása alapvető fontosságú a lasszóelemzés szempontjából. Válasszon egy kis büntetési paramétert, és megkockáztathatja, hogy túl sok változó szerepeljen a modelljében. Válasszon nagyot, és kizárhatja a fontos változókat.
Most a Bayes-i információs kritérium (BIC) segítségével kiválaszthatjuk a büntetési paramétereket a lasszóval kapcsolatos parancsokban mind az előrejelzés, mind a következtetés szempontjából.
Az előrejelzéshez kiválaszthatjuk a büntetési paramétereket azáltal, hogy minimalizáljuk a BIC-t lasszóban, gumihálóban és sqrtlasso-ban. A következtetéshez büntetési paramétereket is választhatunk a BIC minimalizálásával a dsregress, dslogit, dspoisson, poregress, pologit, popoisson, poivregress, xporegress, xpologit, xpopoisson, xpoivregress, és telasso fájlokban.
A BIC büntetési paraméterek kiválasztásával készült lasszó után megrajzolhatjuk a BIC függvényt, amely a BIC kritérium értékeit mutatja a büntetési paraméterek rácsán.A diagram megmutatja a minimális BIC-értéket is, amely a kiválasztott büntetési paraméter értéke. A büntetési paraméterek BIC alapján történő kiválasztásához csak adja meg az opcióválasztást (bic). Az y, lineáris modelljéhez, az x1-x100, kovariánsok jelöltjével, hogy a BIC-t használjuk a kiválasztáshoz, beírjuk
. lasso linear y x1-x100, selection(bic)
Az illesztett BIC függvénydiagram megtekintéséhez beírjuk
. bicplot
A d1 y-ra gyakorolt hatásának becsléséhez és teszteléséhez dupla szelekció használata x1 és x100, kontrollváltozókkal ugyanolyan egyszerű; begépeljük
. dsregress y d1, controls(x1-x100) selection(bic)
Ismét használhatunk bicplot -ot utána.
Kiemelt
- BIC büntetési paraméterek kiválasztása lassoval az előrejelzéshez
- Lasso
- Négyzetgyök lasso
- Elasztikus háló
- BIC büntetési paraméter kiválasztása lasszóval a következtetéshez
- Becslések felosztása
- Keresztillesztéses részleges kiértékelés
- Dupla szelekciós becslők
- BIC büntetési paraméter lasso kezelés-hatás becsléssel
- Ábrázolja a BIC funkciót
Lássuk hogyan működik
BIC használata lasszóban az előrejelzéshez
A lasszóval használt adatkészletek általában sok változóval rendelkeznek. Az induláshoz a vl változókezelő eszközt használjuk, hogy megmentsük magunkat a sok változó nevének manuális beírásától.
. use https://www.stata-press.com/data/r17/fakesurvey_vl (Fictitious survey data with vl) . vl rebuild Rebuilding vl macros ...
| Macro's contents | ||
| Macro | # Vars Description | |
| System | ||
| $vldummy | 98 0/1 variables | |
| $vlcategorical | 16 categorical variables | |
| $vlcontinuous | 29 continuous variables | |
| $vluncertain | 16 perhaps continuous, perhaps categorical variables | |
| $vlother | 12 all missing or constant variables | |
| User | ||
| $demographics | 4 variables | |
| $factors | 110 variables | |
| $idemographics | factor-variable list | |
| $ifactors | factor-variable list | |
A vl létrehozott egy globális makrók halmazát, mindegyik változókészlettel, amelyet felhasználhatunk a becslés során. A vl megkönnyíti az életet, ha nagy mennyiségű kovariánssal van dolgod.
Ezután a splitsample segítségével osztjuk fel az adatokat edzési adatokra és tesztelési adatokra. Az edzésadatokat a lasso modellhez való illesztésre, a tesztelési adatokat pedig az illesztett modell előrejelzési teljesítményének értékelésére használják.
. set seed 12345671 . splitsample, generate(sample) nsplit(2) . label define svalues 1 "Training" 2 "Testing" . label values sample svalues
Most már készen állunk egy lasszó modell beillesztésére a BIC segítségével a büntetési paraméter kiválasztásához. Ehhez meg kell adnunk a selection(bic) opciót.
. lasso linear q104 ($idemographics) $ifactors $vlcontinuous
> if sample == 1, selection(bic)
Evaluating up to 100 lambdas in grid ...
Grid value 1: lambda = 1.059075 no. of nonzero coef. = 4
BIC = 2653.83
Grid value 2: lambda = .96499 no. of nonzero coef. = 5
BIC = 2654.907
...(output omitted)...
Grid value 17: lambda = .2390354 no. of nonzero coef. = 44
BIC = 2663.639
... selection BIC complete ... minimum found
Lasso linear model No. of obs = 458
No. of covariates = 273
Selection: Bayesian information criterion
| No. of | ||
| nonzero Out-of-sample | ||
| ID | Description lambda coef. R-squared BIC | |
| 1 | first lambda 1.059075 4 0.0339 2653.83 | |
| 10 | lambda before .4584484 17 0.2552 2614.289 | |
| * 11 | selected lambda .4177211 18 0.2806 2604.524 | |
| 12 | lambda after .3806119 21 0.3066 2606.103 | |
| 17 | last lambda .2390354 44 0.4220 2663.639 | |
A minimális BIC kritérium által kiválasztott büntetési paraméter 0,42 volt.
A beépített BIC függvénydiagramot megnézhetjük a bicplot beírásával.
. bicplot
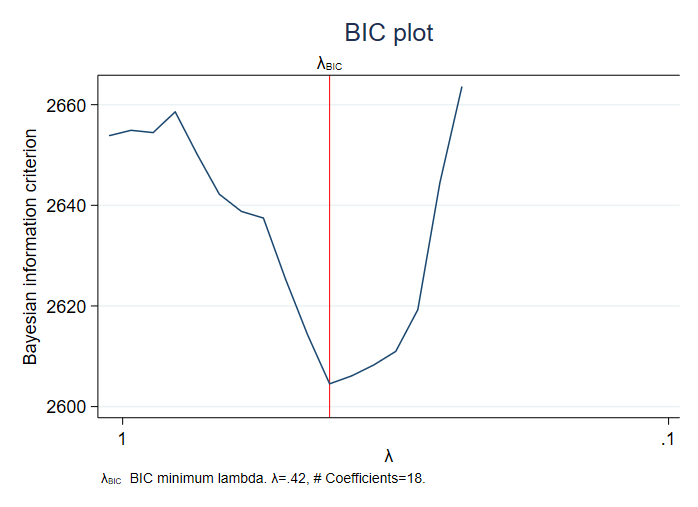
A BIC függvény gyorsan csökken a minimum előtt λ = 0,42-nél.
A BIC használata a dsregress-ben a következtetéshez
Tegyük fel, hogy érdekel minket a levegőszennyezés (no2_class) hatása a gyermekek reakcióidejére (react), a kovariátok ellenőrzése. Abban azonban bizonytalanok vagyunk, hogy melyik kontrollváltozókat vegyük be a modellbe. A dsregress segítségével következetesen megbecsülhetjük a no2_class együtthatóját, míg a vezérlő változók kiválasztásához lasso-t használunk.
Megadjuk azt a selection(bic) opciót, amellyel a bic segítségével kiválaszthatjuk a büntetési paramétereket minden egyes lasóban, amelyet a dsregress végez. 32 globális makrót tárolunk a cc és fc globális makrókban.
. dsregress react no2_class, controls($cc i.($fc)) selection(bic)
Estimating lasso for react using BIC
Estimating lasso for no2_class using BIC
Double-selection linear model Number of obs = 1,036
Number of controls = 32
Number of selected controls = 11
Wald chi2(1) = 22.18
Prob > chi2 = 0.0000
| Robust | ||
| react | Coefficient std. err. z P>|z| [95% conf. interval] | |
| no2_class | 2.315295 .4916547 4.71 0.000 1.35167 3.278921 | |
Látjuk, hogy a 32 kontroll közül 11 van kiválasztva. Pontértékelésünk a nitrogén-dioxid reakcióidőre gyakorolt hatására 2.3, vagyis azt várjuk, hogy a reakcióidő 2.3 milliszekundummal növekszik minden mikrogramm / köbméter nitrogén-dioxid növekedés esetén. Ez az érték statisztikailag eltér a 0-tól. A dsregress valójában két lasztót futtatott, egyet a react és egyet a no2_class-hoz. Gépeléssel ábrázolhatjuk mindkét lassos BIC funkcióját
. bicplot, for(react)
és
. bicplot, for(no2_class)
