Хочете знайти найкращу модель ARIMA або ARFIMA для ваших даних? Порівняйте потенційні моделі за допомогою AIC, BIC та HQIC. Використовуйте нові команди arimasoc та arfimasoc, щоб вибрати найкращу кількість членів авторегресії та ковзного середнього.
Дослідники, які використовують моделі авторегресії та ковзного середнього (ARMA), повинні вирішити, яку кількість лагів слід включити для параметрів авторегресії та ковзного середнього у своїх моделях. Вибір максимальної кількості лагів часто визначається інформаційними критеріями, які балансують між придатністю моделі та її економністю.
arimasoc та arfimasoc допомагають у виборі моделі, підбираючи набір моделей авторегресії з інтегрованим ковзним середнім (ARIMA) або авторегресії з дробово-інтегрованим ковзним середнім (ARFIMA) та обчислюючи інформаційні критерії для кожної моделі. arimasoc та arfimasoc обчислюють інформаційний критерій Акаіке (AIC), інформаційний критерій Байєса (BIC) та інформаційний критерій Ханнана-Квінна (HQIC). Обраною моделлю є та, що має найнижче значення інформаційного критерію.
Подивимося, як це працює
Ми хотіли б підібрати модель ARMA для розриву випуску. Ми використовуємо arimasoc для підбору моделей-кандидатів з максимальним лагом авторегресії 4 і максимальним лагом ковзного середнього 3.
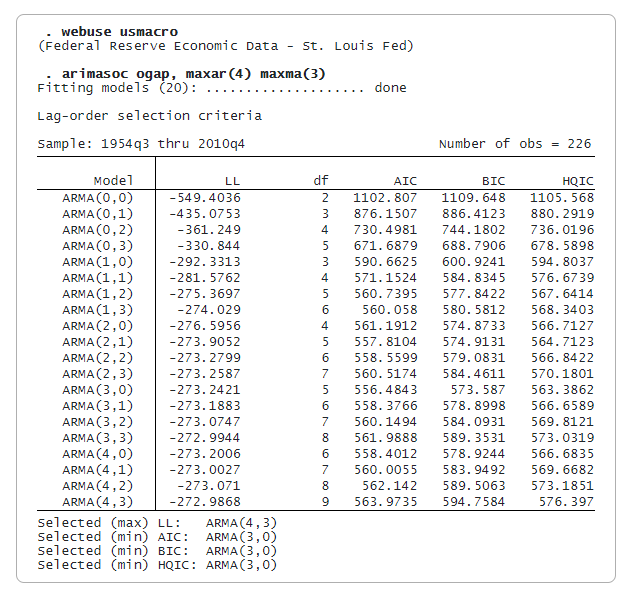
Таблиця результатів містить інформацію про кожну модель, включаючи максимальну логістичну ймовірність, кількість оцінених параметрів, а також AIC, BIC та HQIC.
Під таблицею результатів перелічено обрані моделі за кожним критерієм. Логістична правдоподібність є максимальною для моделі з найбільшою кількістю параметрів – ARMA(4,3). AIC, BIC та HQIC обирають для розриву випуску більш економну модель ARMA(3,0). Тепер ми можемо підігнати нашу обрану модель
. arima ogap, arima(3,0,0) (output omitted)
і переходимо до дослідження модельних передбачень, прогнозів тощо.
Підбір моделі ARFIMA замість моделі ARIMA? Замість того, щоб вводити
. arimasoc y, maxvar(4) maxma(3)
ти набираєш
. arfimasoc y, maxvar(4) maxma(3)

