Nouveau dans 
BIC pour la sélection de la pénalité lasso
La sélection du paramètre de pénalité est fondamentale pour l’analyse lasso. Choisissez un petit paramètre de pénalité, et vous risquez d’inclure trop de variables dans votre modèle. Choisissez-en un grand, et vous risquez d’exclure des variables importantes.
Maintenant, nous pouvons utiliser le critère d’information bayésien (BIC) pour sélectionner les paramètres de pénalité dans les commandes liées à lasso pour la prédiction et l’inférence.
Pour la prédiction, nous pouvons choisir les paramètres de pénalité en minimisant le BIC dans lasso, elasticnet et sqrtlasso. Pour l’inférence, nous pouvons également choisir les paramètres de pénalité en minimisant le BIC dans dsregress, dslogit, dspoisson, poregress, pologit, popoisson, poivregress, xporegress, xpologit, xpopoisson, xpoivregress et telasso.
Après la sélection du lasso avec le paramètre de pénalité BIC, nous pouvons tracer la fonction BIC, qui montre les valeurs du critère BIC sur la grille des paramètres de pénalité. Le graphique montre également le BIC minimum, qui correspond à la valeur du paramètre de pénalité sélectionné.
Pour choisir les paramètres de pénalité en fonction du BIC, il suffit de spécifier l’option selection(bic).
Pour un modèle linéaire pour y, avec des covariables candidates x1-x100, pour utiliser le BIC pour la sélection, nous tapons
. lasso linear y x1-x100, selection(bic)
To look at the fitted BIC function plot, we type
. bicplot
Utiliser la double sélection pour estimer et tester l’effet de d1 sur y, avec les variables de contrôle x1 à x100, est tout aussi simple ; nous tapons
. dsregress y d1, controls(x1-x100) selection(bic)
Encore une fois, nous pouvons utiliser bicplot après.
Points forts
- Sélection des paramètres de pénalité BIC avec lasso pour la prédiction
- Lasso
- Lasso à racine carrée
- Réseau élastique
- Sélection des paramètres de pénalité BIC avec lasso pour l’inférence
- Estimateurs à sortie partielle
- Estimateurs partiels à ajustement croisé
- Estimateurs à double sélection
- Paramètre de pénalité BIC avec estimation de l’effet de traitement avec lasso
- Tracez la fonction BIC
Voyons comment cela fonctionne
Utilisation du BIC dans le lasso pour la prédiction
Les jeux de données utilisés avec lasso comportent généralement de nombreuses variables. Pour commencer, nous utilisons l’outil de gestion des variables vl pour nous éviter de taper manuellement de nombreux noms de variables.
. use https://www.stata-press.com/data/r17/fakesurvey_vl (Fictitious survey data with vl) . vl rebuild Rebuilding vl macros ...
| Macro's contents | ||
| Macro | # Vars Description | |
| System | ||
| $vldummy | 98 0/1 variables | |
| $vlcategorical | 16 categorical variables | |
| $vlcontinuous | 29 continuous variables | |
| $vluncertain | 16 perhaps continuous, perhaps categorical variables | |
| $vlother | 12 all missing or constant variables | |
| User | ||
| $demographics | 4 variables | |
| $factors | 110 variables | |
| $idemographics | factor-variable list | |
| $ifactors | factor-variable list | |
vl a créé un ensemble de macros globales, chacune avec un ensemble de variables que nous pouvons utiliser pendant l’estimation. vl facilite la vie lorsque vous avez affaire à de grands ensembles de covariables.
Ensuite, nous utilisons splitsample pour diviser les données en données d’entraînement et en données de test. Les données d’entraînement seront utilisées pour ajuster le modèle lasso, et les données de test seront utilisées pour évaluer les performances de prédiction du modèle ajusté.
. set seed 12345671 . splitsample, generate(sample) nsplit(2) . label define svalues 1 "Training" 2 "Testing" . label values sample svalues
Maintenant, nous sommes prêts à ajuster un modèle lasso en utilisant le BIC pour sélectionner le paramètre de pénalité. Pour ce faire, nous devons spécifier l’option selection(bic).
. lasso linear q104 ($idemographics) $ifactors $vlcontinuous
> if sample == 1, selection(bic)
Evaluating up to 100 lambdas in grid ...
Grid value 1: lambda = 1.059075 no. of nonzero coef. = 4
BIC = 2653.83
Grid value 2: lambda = .96499 no. of nonzero coef. = 5
BIC = 2654.907
...(output omitted)...
Grid value 17: lambda = .2390354 no. of nonzero coef. = 44
BIC = 2663.639
... selection BIC complete ... minimum found
Lasso linear model No. of obs = 458
No. of covariates = 273
Selection: Bayesian information criterion
| No. of | ||
| nonzero Out-of-sample | ||
| ID | Description lambda coef. R-squared BIC | |
| 1 | first lambda 1.059075 4 0.0339 2653.83 | |
| 10 | lambda before .4584484 17 0.2552 2614.289 | |
| * 11 | selected lambda .4177211 18 0.2806 2604.524 | |
| 12 | lambda after .3806119 21 0.3066 2606.103 | |
| 17 | last lambda .2390354 44 0.4220 2663.639 | |
Le paramètre de pénalité sélectionné par le critère BIC minimum était de 0,42.
Nous pouvons regarder le graphique de la fonction BIC ajustée en tapant bicplot.
. bicplot
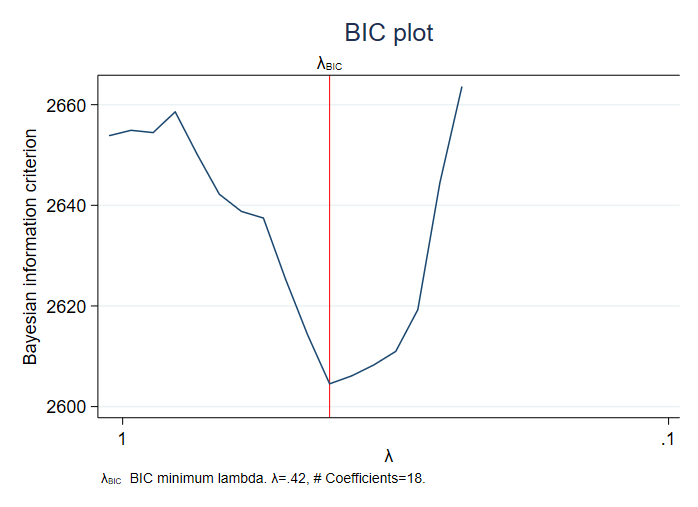
La fonction BIC diminue rapidement avant le minimum à λ=0.42.
Utilisation du BIC dans dsregress pour l’inférence
Supposons que nous souhaitions connaître l’effet de la pollution atmosphérique (no2_class) sur le temps de réaction des enfants (react), en contrôlant les covariables. Cependant, nous ne sommes pas certains des variables de contrôle à inclure dans le modèle. Nous pouvons utiliser dsregress pour estimer de manière cohérente le coefficient sur no2_class tout en utilisant lasso pour sélectionner les variables de contrôle.
Nous spécifions l’option selection(bic) pour utiliser bic afin de sélectionner le paramètre de pénalité dans chaque lasso effectué par dsregress. Nous incluons un ensemble de 32 contrôles stockés dans les macros globales cc et fc.
. dsregress react no2_class, controls($cc i.($fc)) selection(bic)
Estimating lasso for react using BIC
Estimating lasso for no2_class using BIC
Double-selection linear model Number of obs = 1,036
Number of controls = 32
Number of selected controls = 11
Wald chi2(1) = 22.18
Prob > chi2 = 0.0000
| Robust | ||
| react | Coefficient std. err. z P>|z| [95% conf. interval] | |
| no2_class | 2.315295 .4916547 4.71 0.000 1.35167 3.278921 | |
Nous voyons que 11 des 32 contrôles sont sélectionnés. Notre estimation ponctuelle de l’effet du dioxyde d’azote sur le temps de réaction est de 2,3, ce qui signifie que nous nous attendons à ce que le temps de réaction augmente de 2,3 millisecondes pour chaque microgramme par mètre cube d’augmentation du dioxyde d’azote. Cette valeur est statistiquement différente de 0.
dsregress a en fait exécuté deux lassos, un pour react et un pour no2_class. Nous pouvons tracer la fonction BIC pour les deux lassos en tapant
. bicplot, for(react)
and
. bicplot, for(no2_class)
