Нове в 
Байєсівські поздовжні/панельні моделі
Ви можете встановити поздовжні байєсівські моделі/моделі панелі даних, просто додавши до своїх класичних моделей панельних даних префікс bayes:. Оскільки моделі панельних даних можна розглядати як дворівневі ієрархічні моделі, усі переваги байєсівського багаторівневого моделювання також застосовуються до моделей панельних даних.
Ви можете встановити лінійну модель панелі даних із випадковими ефектами до результату y з предикторами x1 і x2 та ідентифікатором панелі або групи id, ввівши
. xtset id . xtreg y x1 x2
Тепер ви можете встановити байєсівський аналог цієї моделі, ввівши
. xtset id . bayes: xtreg y x1 x2
Звичайно, як і з будь-якою іншою командою Stata, ви можете використовувати інтерфейс «наведи і клацни» замість того, щоб вводити команди.
Байєсівські моделі панельних даних призначені не лише для безперервних результатів. Ви можете так само легко вводити двійкові результати
. bayes: xtprobit y x1 x2
або для підрахунку результатів
. bayes: xtpoisson y x1 x2
Або скористайтеся будь-якою з восьми моделей даних панелі, які підтримують префікс bayes, включаючи нову мультиноміальну логіт-модель панельних даних.
Давайте подивимося, як це працює
- Оцінка
- Конвергенція MCMC
- Спеціальні приори
- Задні розподіли ефектів панелі або групи
- Байєсівські передбачення
- Задні прогностичні перевірки — відповідність моделі
- Прибирати
Оцінка
Розглянемо підгрупу даних Національного поздовжнього опитування молодих жінок від 14 до 24 років у 1968 році, які жили на півдні країни. Будемо моделювати журнал заробітної плати як функцію освіти особи, grade; їхній досвід роботи, ttl_exp, що входить до моделі квадратично; і чи живуть вони в стандартній мегаполісі, not_smsa. Існує кілька спостережень на кожну людину, ідентифікованих за допомогою id.
Ми підбираємо байєсівську лінійну модель даних панелі для врахування окремих ефектів. Ми також хочемо обчислити байєсівські прогнози заробітної плати та порівняти індивідуальні (панельні) ефекти.
. webuse nlswork6 (Subsample of 1986 National Longitudinal Survey of Young Women)
Щоб заощадити час, ми запускаємо вибірку ланцюга Маркова Монте-Карло (MCMC) із 1000 замість стандартних 10000. Ми також вказуємо початкове число випадкових чисел для відтворюваності.
. bayes, mcmcsize(1000) rseed(17): xtreg ln_wage grade c.ttl_exp##c.ttl_exp i.not_smsa
note: Gibbs sampling is used for regression coefficients and variance
components.
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aaaaa done
Simulation 1000 .........1000 done
Model summary
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| ln_wage | ||
| grade | .0696248 .0052371 .00082 .069638 .0591421 .07999 | |
| ttl_exp | .0404646 .0070371 .000544 .0404901 .026454 .053855 | |
| c.ttl_exp# | ||
| c.ttl_exp | -.0005053 .0003978 .000039 -.0005132 -.0012609 .0003009 | |
| 1.not_smsa | -.1502314 .0251494 .002755 -.150213 -.200979 -.1014476 | |
| _cons | .5646936 .0658804 .0099 .5680976 .4377888 .6957415 | |
| var_U | .0801363 .0073138 .001258 .0795163 .0674855 .0959143 | |
| sigma2 | .0673308 .0046724 .000952 .0671238 .0590742 .0771401 | |
Попереднє середнє значення коефіцієнта grade є позитивним і становить 7 відсотків. Теорія припускає, що заробітна плата зростає з досвідом, але збільшення з часом зменшується. Це означає, що коефіцієнт для ttl_exp має бути додатним, а коефіцієнт для c.ttl_exp#c.ttl_exp має бути негативним. Це ми спостерігаємо в наших даних. Нарешті, проживання за межами великих міських центрів негативно впливає на заробітну плату.
Байєсовське моделювання вимагає, щоб ви вказали пріоритети для всіх параметрів моделі. Як і будь-яка інша команда bayes, bayes: xtreg для зручності надає пріоритети за замовчуванням. Вам слід переглянути попередні специфікації та вказати власні.
Конвергенція MCMC
bayes: xtreg використовує MCMC для отримання результатів. Перед подальшим аналізом необхідно перевірити його збіг. Ви можете зробити це графічно, або ви можете обчислити статистику збіжності Гельмана–Рубіна, використовуючи декілька ланцюжків.
Давайте оцінимо конвергенцію MCMC візуально для, скажімо, коефіцієнта grade.
. bayesgraph diagnostics {ln_wage:grade}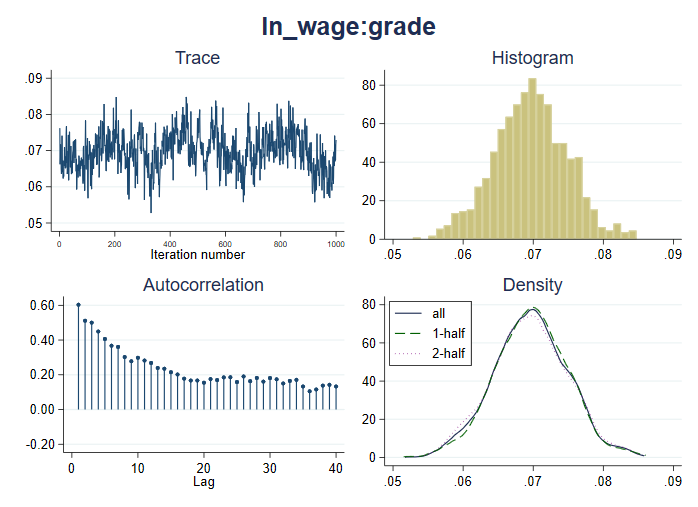
У сюжеті сліду немає явної тенденції. Автокореляція з часом зменшується. У нас немає підстав підозрювати несходження для grade, але збіжність потрібно перевірити для всіх параметрів моделі.
Давайте збережемо наш MCMC та результати оцінки для подальшого використання.
. bayes, saving(bxtregsim) note: file bxtregsim.dta saved. . estimates store bxtreg
Спеціальні приори
З байєсівськими моделями ви можете включити свої власні пріоритети. Ці пріоритети часто беруться з історичних даних. Наприклад, на основі попередніх досліджень може бути розумно припустити, що коефіцієнт для grade коливається від 0 до 25. Тому ми можемо розглянути рівномірне значення (0,25) до цього. Ми можемо використовувати параметр prior() Байеса, щоб вказати власні пріоритети.
. bayes, mcmcsize(1000) rseed(17) prior({ln_wage:grade}, uniform(0,25)):
> xtreg ln_wage grade c.ttl_exp##c.ttl_exp i.not_smsa
note: Gibbs sampling is used for variance components.
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aaaaa done
Simulation 1000 .........1000 done
Model summary
| Equal-tailed | ||
| Mean Std. dev. MSCE Median [95% cred. interval] | ||
| ln_wage | ||
| grade | .0691558 .0063225 .002013 .0692614 .0567288 .0819581 | |
| ttl_exp | .0389882 .0080916 .002355 .0390646 .0228502 .0530886 | |
| c.ttl_exp# | ||
| c.ttl_exp | -.0004548 .0004804 .000153 -.0004778 -.0013733 .0005973 | |
| 1.not_smsa | -.1452854 .0241483 .006649 -.1450175 -.1934294 -.0947368 | |
| _cons | .5751218 .0727991 .022234 .5795395 .4176046 .7018132 | |
| var_U | .0785815 .0082846 .00198 .0784331 .0615956 .0956798 | |
| sigma2 | .0688682 .0059815 .001537 .0684258 .0583475 .0823034 | |
Наша попередня версія не сильно змінила результати.
Задні розподіли ефектів панелі або групи
Нам може бути цікаво зробити висновок про вплив окремих осіб (групи). Байєсівське моделювання забезпечує природний спосіб зробити це. На відміну від класичних моделей панельних даних із випадковими ефектами, байєсівські моделі панельних даних оцінюють випадкові (панельні) ефекти разом з усіма іншими параметрами моделі. Таким чином, кожен випадковий ефект представлений цілим зразком MCMC з його заднього розподілу. Цей зразок можна використовувати для висновків, таких як порівняння панелей або групових ефектів. (Подумайте про порівняння ефективності різних компаній або лікарень.)
Давайте повернемося до нашої вихідної моделі, яка використовувала неінформативні априори за замовчуванням.
. estimates restore bxtreg (results bxtreg are active now)
Давайте побудуємо графік апостеріорних розподілів для перших дев’яти окремих ефектів.
. bayesgraph histogram {U[1/9]}, byparm normal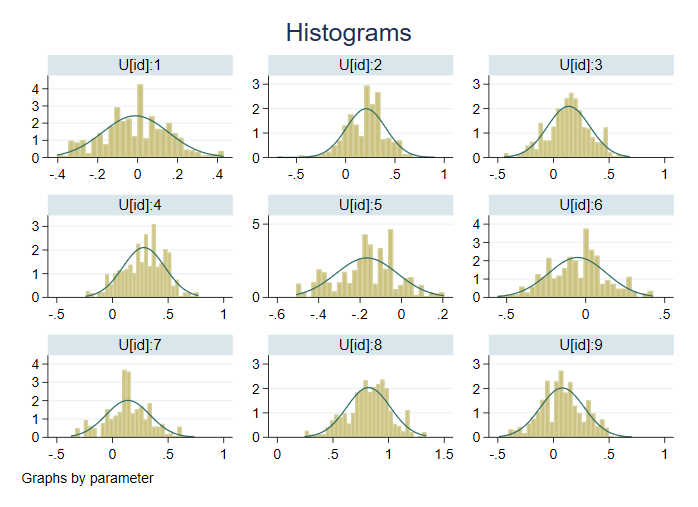
Наведені вище індивідуальні ефекти являють собою зсув або зміщення від середньої заробітної плати. Безперечно, існують відмінності між зарплатами окремих осіб. Наприклад, ми бачимо, що заробітна плата особи 8 вища, ніж індивідуальна 5. Таким чином, все ще існують відмінності між окремими зарплатами, які не враховуються прогнозниками моделі.
Байєсівські передбачення
У рамках байєсівської системи ви можете обчислювати передбачення та їх невизначеність, не роблячи жодних асимптотичних припущень. Це можливо, оскільки отримані прогнози є вибірками з «точного» апостеріорного прогнозного розподілу нових даних з урахуванням спостережуваних даних. Задній прогнозний розподіл не вважається асимптотично нормальним.
Давайте обчислимо апостеріорні середні передбачуваної заробітної плати разом із їхнім 95% достовірним інтервалом
. bayespredict pmean, mean Computing predictions ... . bayespredict cri_l cri_u, cri Computing predictions ...
Давайте перерахуємо результати перших 10 спостережень.
. list ln_wage pmean cri_l cri_u in 1/10
| ln_wage pmean cri_l cri_u | ||||
| 1. | 1.543923 1.55197 .8831815 2.184215 | |||
| 2. | 1.815738 1.645933 1.006488 2.284888 | |||
| 3. | 1.870532 1.718343 1.112855 2.360129 | |||
| 4. | 2.340405 2.16819 1.523068 2.747879 | |||
| 5. | 1.545327 1.629953 1.092535 2.221188 | |||
| 6. | 1.594335 1.687503 1.089151 2.268714 | |||
| 7. | 1.848619 1.849651 1.266758 2.408907 | |||
| 8. | 1.757637 1.80307 1.140366 2.467546 | |||
| 9. | 2.346746 2.224904 1.529079 2.833333 | |||
| 10. | 3.539868 2.826903 2.270285 3.511156 | |||
Передбачені апостеріорні середні є близькими до спостережуваних значень, за винятком, можливо, спостереження 10. У наступному розділі ми покажемо, як перевірити, чи модель добре підходить більш формально. Але для цього ми повинні спочатку зберегти всі передбачення MCMC.
. bayespredict {_ysim1}, saving(bxtregpred)
Computing predictions ...
file bxtregpred.dta saved.
file bxtregpred.ster saved.
bxtregpred.dta містить вибірку значень MCMC для кожного спостереження. Задні середні ((pmean), які ми передбачили раніше, для кожного спостереження є середніми за вибіркою MCMC.
Набори даних прогнозів MCMC, як правило, великі, тому ви можете розглянути можливість збереження їх лише за необхідності; див. [BAYES] bayespredict для деталей.
Задні прогностичні перевірки — відповідність моделі
Ще однією перевагою байєсіанського аналізу моделей панельних даних є формалізовані попередні прогнозні перевірки для перевірки відповідності моделі, які недоступні при класичному частотистському аналізі.
Ми можемо використовувати апостеріорні вибірки для прогнозованого результату, вибірку передбачення MCMC, щоб виконати перевірку відповідності моделі. Наприклад, давайте порівняємо мінімальну та максимальну статистику з вибірок прогнозу MCMC з тими, що спостерігаються в даних. Ця статистика описує хвости розподілу даних. Ви можете використовувати будь-яку іншу статистику замість (або на додаток до) максимуму та мінімуму.
bayesstats ppvalues виконує попередні прогнозні перевірки шляхом обчислення так званих апостеріорних прогнозних p-значень (PPPs). PPP описують, як часто статистичні дані з вибірки прогнозування MCMC були такими ж екстремальними або більш екстремальними, ніж у вибірці, що спостерігається; див. [BAYES] bayesstats ppvalues.
. bayesstats ppvalues (pmin:@min({_ysim1})) (pmax:@max({_ysim1})) using bxtregpred
Posterior predictive summary MCMC sample size = 1,000
| T | Mean Std. dev. E(T_obs) P(T>=T_obs) | |
| pmin | .0299837 .1652143 .0176546 .565 | |
| pmax | 3.515637 .2291669 3.85025 .085 | |
PPP для мінімуму, 0,565, не близький до 0 або 1, тому модель добре відповідає цій статистиці. Але PPP для максимуму, 0,085, близький до 0 і, таким чином, свідчить про те, що він погано підходить для цієї статистики.
Якщо ми вивчимо дані, ми виявимо кластер спостережень із значеннями від 3,5 до 4, які виглядають як викиди. Можливо, нам доведеться переглянути нашу модель і вирішити проблему викидів.
Прибирати
Після аналізу ми можемо видалити файли, створені bayes: var і bayespredict, які більше не потрібні.
. erase bxtregsim.dta . erase bxtregpred.dta . erase bxtregpred.ster
